2020-2021学年华东师大版八年级下册19.1.1 矩形的性质课件(共17张)
文档属性
| 名称 | 2020-2021学年华东师大版八年级下册19.1.1 矩形的性质课件(共17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 247.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 10:58:17 | ||
图片预览




文档简介
第1课时 矩形及其性质
第19章 矩形、菱形与正方形
19.1 矩 形
什么是平行四边形?
平行四边形都有哪些性质?
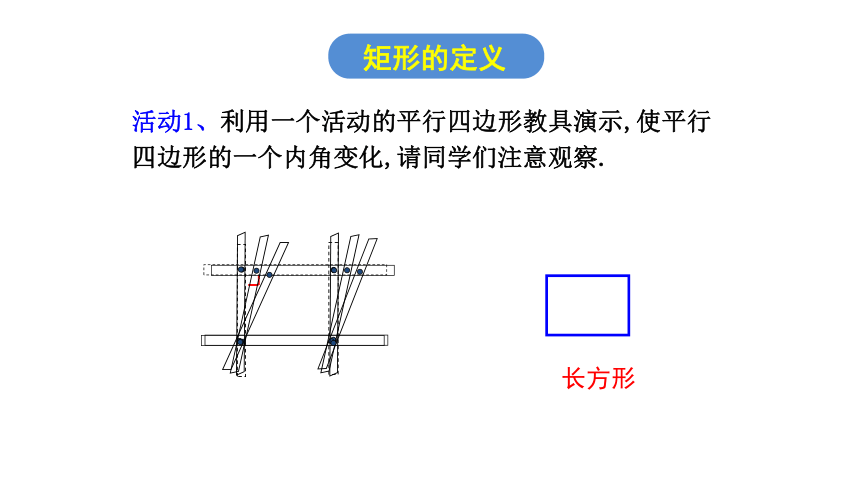
活动1、利用一个活动的平行四边形教具演示,使平行四边形的一个内角变化,请同学们注意观察.
长方形
矩形的定义
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形.
定义:有一个角是直角的平行四边形叫做矩形,也就是长方形.
平行四边形不一定是矩形.
例1
下列说法正确的是( )
A.平行四边形是矩形
B.矩形不一定是平行四边形
C.有一个角是直角的四边形是矩形
D.平行四边形具有的性质矩形都具有
D
思考 因为矩形是平行四边形,所以它具有平行四边形的所有性质,由于它有一个角为直角,它是否具有一般平行四边形不具有的一些特殊性质呢?
可以从边,角,对角线等方面来考虑.
矩形的边角性质
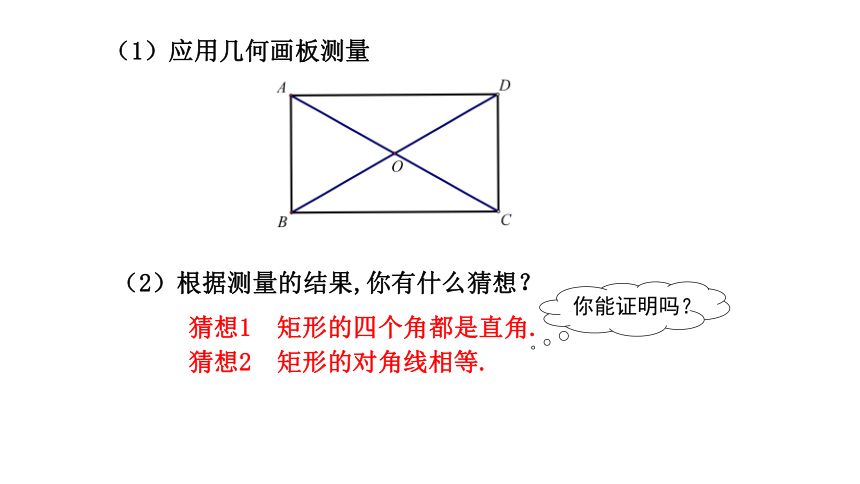
(2)根据测量的结果,你有什么猜想?
猜想1 矩形的四个角都是直角.
猜想2 矩形的对角线相等.
你能证明吗?
(1)应用几何画板测量
证明:由定义,矩形必有一个角是直角,
设∠A = 90°
∵AB∥DC,AD∥BC,
∴∠B=∠C=∠D =90°.
(两直线平行,同旁内角互补)
即矩形ABCD的四个角都是直角.
已知,矩形ABCD.
求证: ∠A=∠B=∠C=∠D=90°.
A
B
C
D
证一证
证明:∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
在△ABC和△DCB中,
∵AB=DC,∠ABC=∠DCB,BC= CB,
∴△ABC≌△DCB.
∴AC=DB.
A
B
C
D
O
如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相交于点O.
求证:AC=DB.
思考:矩形是不是中心对称图形? 如果是,那么对称中心是什么?
矩形是中心对称图形,对角线的交点是它的对称中心.
由于矩形是平行四边形,因此
O
矩形性质:
(1)从边看:对边平行且相等;
(2)从角看:四个角都是直角;
(3)从对角线看:对角线相等;
(4)对称性:是中心对称图形,也是轴对称图形,邻边不相等的矩形有两条对称轴;
(5)面积:矩形的面积=长×宽;
矩形的面积=被对角线分成的四个等面积的小三角
形面积之和,
注:这四个小三角形是两对全等的等腰三角形.
归纳总结
例2
如图,在矩形ABCD中,AB =3,BC =4,BE⊥AC,垂足为点 E. 试求BE 的长.
在矩形ABCD中, ∠ABC = 90°,
解:
又∵S△ABC
例3 如图,在矩形ABCD中,两条对角线AC,BD相交于点O,∠AOB=60°,AB=4 ,求矩形对角线的长.
解:∵四边形ABCD是矩形.
∴AC = BD,
OA= OC= AC,OB = OD = BD ,
∴OA = OB.
又∵∠AOB=60°,
∴△OAB是等边三角形,
∴OA=AB=4,
∴AC=BD=2OA=8.
A
B
C
D
O
例4
如图,在矩形ABCD中,对角线AC与BD相交于点O,AE垂直且平分线段BO,垂足为点E,BD=15 cm.
求AC、AB的长.
∵四边形ABCD是矩形,
∴AC=BD=15(矩形的
对角线相等),
∴AO= AC=7. 5.
∵AE垂直平分BO,
∴AB=AO=7. 5.
即AC的长为15 cm,AB的长为7. 5 cm.
解:
例5
矩形ABCD被两条对角线分成四个小三角形, 如果四个小三角形周长的和是86 cm, 矩形的对角线长是13 cm,那么该矩形的周长是多少?
∵△AOB、△BOC、△COD和△AOD四个小三角
形周长的和为86 cm.
∴AB+BC+CD+DA+2(OA+OB+OC+OD)
=AB+BC+CD+DA+2(AC+BD)
=86.
又∵AC=BD=13(矩形的对角线相等),
∴AB+BC+CD+DA=86-2(AC+BD)=86-4×13=34(cm),
即矩形ABCD的周长等于34 cm.
解:
例6
如图,在矩形ABCD(AB>AD)中,△AOB与△AOD的周长的差为2 cm,和为34 cm,两条对角线长的和为20 cm,求矩形的周长和面积.
由题意得
AC=BD,AO=CO= AC,OB=OD= BD,
∴OA=OB=OC=OD= AC.
∵AC+BD=20 cm,∴AC=BD=10 cm,AO=5 cm.
∵AB+AO+OB+AD+AO+DO=34 cm,
∴AB+AD+2AO+BD=34 cm,∴AB+AD=14 cm.
又∵(AB+AO+BO)-(AD+AO+DO)=2 cm,
∴AB-AD=2 cm,∴AB=8 cm,AD=6 cm,
∴矩形ABCD的周长为2×(8+6)=28(cm),
矩形ABCD的面积为8×6=48(cm2).
解:
1.矩形是特殊的平行四边形,具有平行四边形的所有性
质,它的特殊性就是四个角都是直角和对角线相等.
2.矩形的对角线将矩形分为两对全等的等腰三角形.
在解题的时候常用等腰三角形的性质.
3.矩形既是中心对称图形又是轴对称图形,有两条对称
轴.
第19章 矩形、菱形与正方形
19.1 矩 形
什么是平行四边形?
平行四边形都有哪些性质?
活动1、利用一个活动的平行四边形教具演示,使平行四边形的一个内角变化,请同学们注意观察.
长方形
矩形的定义
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形.
定义:有一个角是直角的平行四边形叫做矩形,也就是长方形.
平行四边形不一定是矩形.
例1
下列说法正确的是( )
A.平行四边形是矩形
B.矩形不一定是平行四边形
C.有一个角是直角的四边形是矩形
D.平行四边形具有的性质矩形都具有
D
思考 因为矩形是平行四边形,所以它具有平行四边形的所有性质,由于它有一个角为直角,它是否具有一般平行四边形不具有的一些特殊性质呢?
可以从边,角,对角线等方面来考虑.
矩形的边角性质
(2)根据测量的结果,你有什么猜想?
猜想1 矩形的四个角都是直角.
猜想2 矩形的对角线相等.
你能证明吗?
(1)应用几何画板测量
证明:由定义,矩形必有一个角是直角,
设∠A = 90°
∵AB∥DC,AD∥BC,
∴∠B=∠C=∠D =90°.
(两直线平行,同旁内角互补)
即矩形ABCD的四个角都是直角.
已知,矩形ABCD.
求证: ∠A=∠B=∠C=∠D=90°.
A
B
C
D
证一证
证明:∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
在△ABC和△DCB中,
∵AB=DC,∠ABC=∠DCB,BC= CB,
∴△ABC≌△DCB.
∴AC=DB.
A
B
C
D
O
如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相交于点O.
求证:AC=DB.
思考:矩形是不是中心对称图形? 如果是,那么对称中心是什么?
矩形是中心对称图形,对角线的交点是它的对称中心.
由于矩形是平行四边形,因此
O
矩形性质:
(1)从边看:对边平行且相等;
(2)从角看:四个角都是直角;
(3)从对角线看:对角线相等;
(4)对称性:是中心对称图形,也是轴对称图形,邻边不相等的矩形有两条对称轴;
(5)面积:矩形的面积=长×宽;
矩形的面积=被对角线分成的四个等面积的小三角
形面积之和,
注:这四个小三角形是两对全等的等腰三角形.
归纳总结
例2
如图,在矩形ABCD中,AB =3,BC =4,BE⊥AC,垂足为点 E. 试求BE 的长.
在矩形ABCD中, ∠ABC = 90°,
解:
又∵S△ABC
例3 如图,在矩形ABCD中,两条对角线AC,BD相交于点O,∠AOB=60°,AB=4 ,求矩形对角线的长.
解:∵四边形ABCD是矩形.
∴AC = BD,
OA= OC= AC,OB = OD = BD ,
∴OA = OB.
又∵∠AOB=60°,
∴△OAB是等边三角形,
∴OA=AB=4,
∴AC=BD=2OA=8.
A
B
C
D
O
例4
如图,在矩形ABCD中,对角线AC与BD相交于点O,AE垂直且平分线段BO,垂足为点E,BD=15 cm.
求AC、AB的长.
∵四边形ABCD是矩形,
∴AC=BD=15(矩形的
对角线相等),
∴AO= AC=7. 5.
∵AE垂直平分BO,
∴AB=AO=7. 5.
即AC的长为15 cm,AB的长为7. 5 cm.
解:
例5
矩形ABCD被两条对角线分成四个小三角形, 如果四个小三角形周长的和是86 cm, 矩形的对角线长是13 cm,那么该矩形的周长是多少?
∵△AOB、△BOC、△COD和△AOD四个小三角
形周长的和为86 cm.
∴AB+BC+CD+DA+2(OA+OB+OC+OD)
=AB+BC+CD+DA+2(AC+BD)
=86.
又∵AC=BD=13(矩形的对角线相等),
∴AB+BC+CD+DA=86-2(AC+BD)=86-4×13=34(cm),
即矩形ABCD的周长等于34 cm.
解:
例6
如图,在矩形ABCD(AB>AD)中,△AOB与△AOD的周长的差为2 cm,和为34 cm,两条对角线长的和为20 cm,求矩形的周长和面积.
由题意得
AC=BD,AO=CO= AC,OB=OD= BD,
∴OA=OB=OC=OD= AC.
∵AC+BD=20 cm,∴AC=BD=10 cm,AO=5 cm.
∵AB+AO+OB+AD+AO+DO=34 cm,
∴AB+AD+2AO+BD=34 cm,∴AB+AD=14 cm.
又∵(AB+AO+BO)-(AD+AO+DO)=2 cm,
∴AB-AD=2 cm,∴AB=8 cm,AD=6 cm,
∴矩形ABCD的周长为2×(8+6)=28(cm),
矩形ABCD的面积为8×6=48(cm2).
解:
1.矩形是特殊的平行四边形,具有平行四边形的所有性
质,它的特殊性就是四个角都是直角和对角线相等.
2.矩形的对角线将矩形分为两对全等的等腰三角形.
在解题的时候常用等腰三角形的性质.
3.矩形既是中心对称图形又是轴对称图形,有两条对称
轴.
