2020-2021学年华东师大版八年级下册20.3.1 方差课件(共14张)
文档属性
| 名称 | 2020-2021学年华东师大版八年级下册20.3.1 方差课件(共14张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 140.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 11:01:20 | ||
图片预览






文档简介
20.3 数据的离散程度
第1课时 方差
在统计学中,除了平均数、中位数、众数这类刻画数
据集中趋势的量以外,还有一类刻画数据波动(离散)程
度的量,其中最重要的就是方差. 本节我们将在实际问题
情境中,了解方差的统计意义并运用方差解决问题.
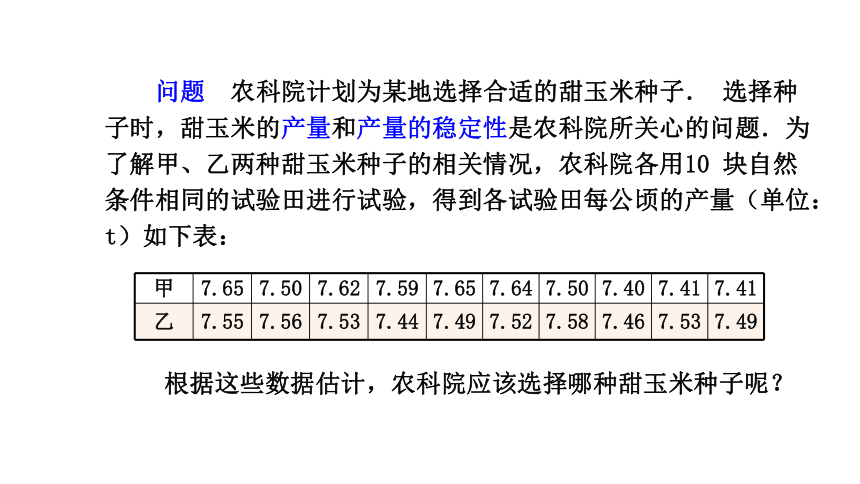
问题 农科院计划为某地选择合适的甜玉米种子. 选择种子时,甜玉米的产量和产量的稳定性是农科院所关心的问题.为了解甲、乙两种甜玉米种子的相关情况,农科院各用10 块自然条件相同的试验田进行试验,得到各试验田每公顷的产量(单位:t)如下表:
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
根据这些数据估计,农科院应该选择哪种甜玉米种子呢?
(1)甜玉米的产量可用什么量来描述?请计算后说明.
说明在试验田中,甲、乙两种甜玉米的平均产量相差不大.
可估计这个地区种植这两种甜玉米的平均产量相差不大.
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
产量波动较大
产量波动较小
(2)如何考察一种甜玉米产量的稳定性呢?
①请设计统计图直观地反映出甜玉米产量的分布情况.
定义:设有n个数据x1,x2,…,xn ,各数据与它们的平均数 的差的平方分别是 … , 我们用这些值的平均数,即用 来衡量这组数据波动的大小,并把它叫做这组数据的方差,记作s2.
注意:
(1)方差是用来衡量一组数据的波动大小的重要量,反映的是数据在平均数附近波动的情况;
(2)对于同类问题的两组数据,方差越大,数据的波动就越大;方差越小,数据的波动就越小.
②请利用方差公式分析甲、乙两种甜玉米产量的波动程度.
两组数据的方差分别是:
据样本估计总体的统计思想,种乙种甜玉米产量较稳定.
显然 > ,即说明甲种甜玉米产量的波动较大,这与我们从产量分布图看到的结果一致.
人数相同的七年级甲、乙两班学生在同一次数学单元测试中,班级平均分和方差如下:
=80,s2甲=190,s2乙=170,则成绩较为稳定的班级是( )
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定
例1
B
一组数据6、4、a、3、2的平均数是5,这组数据的方差为( )
A.8 B.5 C.2 D.3
例2
A
为了考察甲、乙两种黄豆的长势,分别从中抽取了10株麦苗,测得高度(单位:cm)如下:
甲:15,15,14,11,16,14,12,14,13,15;
乙:17,14,12,16,15,14,14,14,13,11.
哪种麦苗长势整齐?
例3
x甲= ×(15+15+…+15)=13.9(cm),
s甲2= ×[(15-13.9)2+(15-13.9)2+…+(15-13.9)2]
=2.09,
x乙= ×(17+14+…+11)=14(cm),
s乙2= ×[(17-14)2+(14-14)2+…+(11-14)2]=2.8,
因为s甲2<s乙2,所以甲种麦苗长势整齐.
解:
-
-
1、两名同学各进行了20次跳远测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位更稳定,通常还需要比较他们成绩的( )
A.众数 B.中位数
C.方差 D.以上都不对
C
课堂练习
2、在某中学举行的知识竞答比赛中,八年级5名参赛选手的成绩如下表所示,请你根据表中提供的数据,计算出这5名选手成绩的方差是( )
A. 2 B.6.8
C.34 D.93
{5940675A-B579-460E-94D1-54222C63F5DA}选
手
1
号
2
号
3
号
4
号
5
号
平均
成绩
得分
90
95
█
89
88
91
B
3.为了从甲、乙两名学生中选择一人去参加电脑知识竞赛,在相同条件下对他们的电脑知识进行10次测验,成绩(单位:分)如下:
甲的成绩
76
84
90
84
81
87
88
81
85
84
乙的成绩
82
86
87
90
79
81
93
90
74
78
填写下表:
同学
平均成绩
中位数
众数
方差
85分以上的频率
甲
84
84
0.3
乙
84
84
34
84
90
0.5
14.4
方差是用来衡量一组数据波动大小的重要统计量,反映
的是数据在平均数附近波动的情况,对于同类问题的两
组数据,方差越大,数据波动就越大,方差越小,数据
波动就越小;在统计中常用样本方差去估计总体方差.
第1课时 方差
在统计学中,除了平均数、中位数、众数这类刻画数
据集中趋势的量以外,还有一类刻画数据波动(离散)程
度的量,其中最重要的就是方差. 本节我们将在实际问题
情境中,了解方差的统计意义并运用方差解决问题.
问题 农科院计划为某地选择合适的甜玉米种子. 选择种子时,甜玉米的产量和产量的稳定性是农科院所关心的问题.为了解甲、乙两种甜玉米种子的相关情况,农科院各用10 块自然条件相同的试验田进行试验,得到各试验田每公顷的产量(单位:t)如下表:
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
根据这些数据估计,农科院应该选择哪种甜玉米种子呢?
(1)甜玉米的产量可用什么量来描述?请计算后说明.
说明在试验田中,甲、乙两种甜玉米的平均产量相差不大.
可估计这个地区种植这两种甜玉米的平均产量相差不大.
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
产量波动较大
产量波动较小
(2)如何考察一种甜玉米产量的稳定性呢?
①请设计统计图直观地反映出甜玉米产量的分布情况.
定义:设有n个数据x1,x2,…,xn ,各数据与它们的平均数 的差的平方分别是 … , 我们用这些值的平均数,即用 来衡量这组数据波动的大小,并把它叫做这组数据的方差,记作s2.
注意:
(1)方差是用来衡量一组数据的波动大小的重要量,反映的是数据在平均数附近波动的情况;
(2)对于同类问题的两组数据,方差越大,数据的波动就越大;方差越小,数据的波动就越小.
②请利用方差公式分析甲、乙两种甜玉米产量的波动程度.
两组数据的方差分别是:
据样本估计总体的统计思想,种乙种甜玉米产量较稳定.
显然 > ,即说明甲种甜玉米产量的波动较大,这与我们从产量分布图看到的结果一致.
人数相同的七年级甲、乙两班学生在同一次数学单元测试中,班级平均分和方差如下:
=80,s2甲=190,s2乙=170,则成绩较为稳定的班级是( )
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定
例1
B
一组数据6、4、a、3、2的平均数是5,这组数据的方差为( )
A.8 B.5 C.2 D.3
例2
A
为了考察甲、乙两种黄豆的长势,分别从中抽取了10株麦苗,测得高度(单位:cm)如下:
甲:15,15,14,11,16,14,12,14,13,15;
乙:17,14,12,16,15,14,14,14,13,11.
哪种麦苗长势整齐?
例3
x甲= ×(15+15+…+15)=13.9(cm),
s甲2= ×[(15-13.9)2+(15-13.9)2+…+(15-13.9)2]
=2.09,
x乙= ×(17+14+…+11)=14(cm),
s乙2= ×[(17-14)2+(14-14)2+…+(11-14)2]=2.8,
因为s甲2<s乙2,所以甲种麦苗长势整齐.
解:
-
-
1、两名同学各进行了20次跳远测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位更稳定,通常还需要比较他们成绩的( )
A.众数 B.中位数
C.方差 D.以上都不对
C
课堂练习
2、在某中学举行的知识竞答比赛中,八年级5名参赛选手的成绩如下表所示,请你根据表中提供的数据,计算出这5名选手成绩的方差是( )
A. 2 B.6.8
C.34 D.93
{5940675A-B579-460E-94D1-54222C63F5DA}选
手
1
号
2
号
3
号
4
号
5
号
平均
成绩
得分
90
95
█
89
88
91
B
3.为了从甲、乙两名学生中选择一人去参加电脑知识竞赛,在相同条件下对他们的电脑知识进行10次测验,成绩(单位:分)如下:
甲的成绩
76
84
90
84
81
87
88
81
85
84
乙的成绩
82
86
87
90
79
81
93
90
74
78
填写下表:
同学
平均成绩
中位数
众数
方差
85分以上的频率
甲
84
84
0.3
乙
84
84
34
84
90
0.5
14.4
方差是用来衡量一组数据波动大小的重要统计量,反映
的是数据在平均数附近波动的情况,对于同类问题的两
组数据,方差越大,数据波动就越大,方差越小,数据
波动就越小;在统计中常用样本方差去估计总体方差.
