2020-2021学年华东师大版八年级下册第17章 函数及其图象 小结与复习课件(共25张)
文档属性
| 名称 | 2020-2021学年华东师大版八年级下册第17章 函数及其图象 小结与复习课件(共25张) |  | |
| 格式 | pptx | ||
| 文件大小 | 860.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 11:06:49 | ||
图片预览










文档简介
小结与复习
第17章 函数及其图象
要点梳理
1. 常量与变量
叫变量,
叫常量.
2.函数定义:
取值发生变化的量
取值固定不变的量
在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
一、函数
3.函数的图象:对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
列表法
解析法
图象法.
5.函数的三种表示方法:
4.描点法画图象的步骤:列表、描点、连线
例1.(1)设圆柱的底面半径R不变,圆柱的体积V与圆柱的高h的关系式是V=πR2h,在这个变化过程中常量和变量分别是什么?
(2)设圆柱的高h不变,在圆柱的体积V与圆柱的底面半径R的关系式V=πR2h中,常量和变量分别又是什么?
解:(1)常量是π和R,变量是V和h.
(2)常量是π和h,变量是V和R.
B
例3、已知点P(m+2,2m-4)在x轴上,则点P的坐标是( )
A.(4,0) B.(0,4)
C.(-4,0) D.(0,-4)
A
例4、点M(a,b)为平面直角坐标系中的点.
(1)当a>0,b<0时,点M位于第几象限?
(2)当ab>0时,点M位于第几象限?
(3)当a为任意非零实数,且b<0时,点M位于第几象限?
解:(1)第四象限.
(2)∵ab>0,
∴a>0且b>0或a<0且b<0.
∴点M位于第一象限或第三象限.
(3)第三象限或第四象限.
例5、已知点A(2,3)在函数y=ax2-x+1的图象上,则a等于( )
A.1 B.-1 C.2 D.-2
A
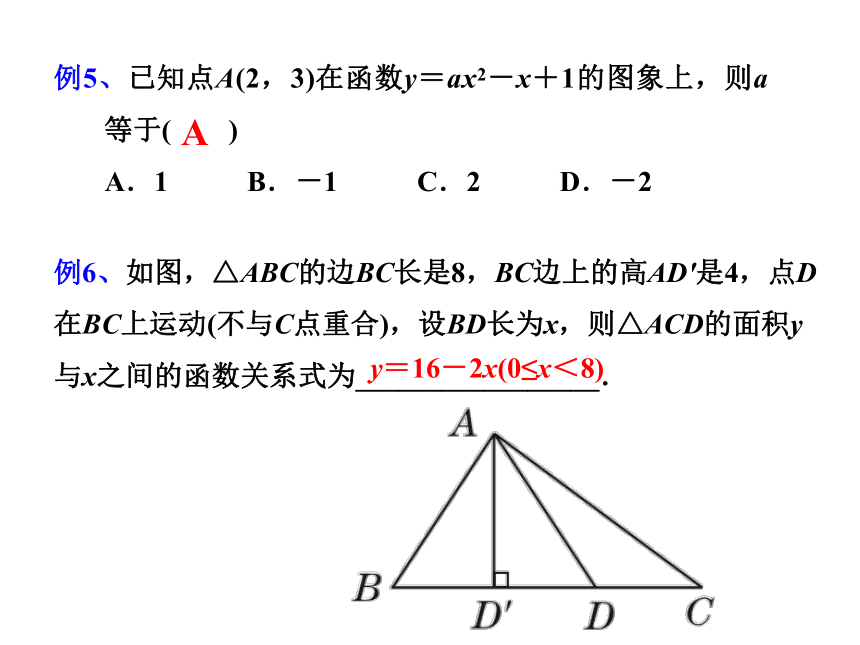
例6、如图,△ABC的边BC长是8,BC边上的高AD′是4,点D在BC上运动(不与C点重合),设BD长为x,则△ACD的面积y与x之间的函数关系式为_________________.
y=16-2x(0≤x<8)
D
变式2、若点(-m,3)与点(-5,n)关于y轴对称,则( )
A.m=-5,n=3
B.m=5,n=3
C.m=-5,n=-3
D.m=-3,n=5
A
变式3、在平面直角坐标系中,将点A(1,-2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,则点B的坐标是( )
A.(-1,1) B.(3,1) C.(4,-4) D.(4,0)
A
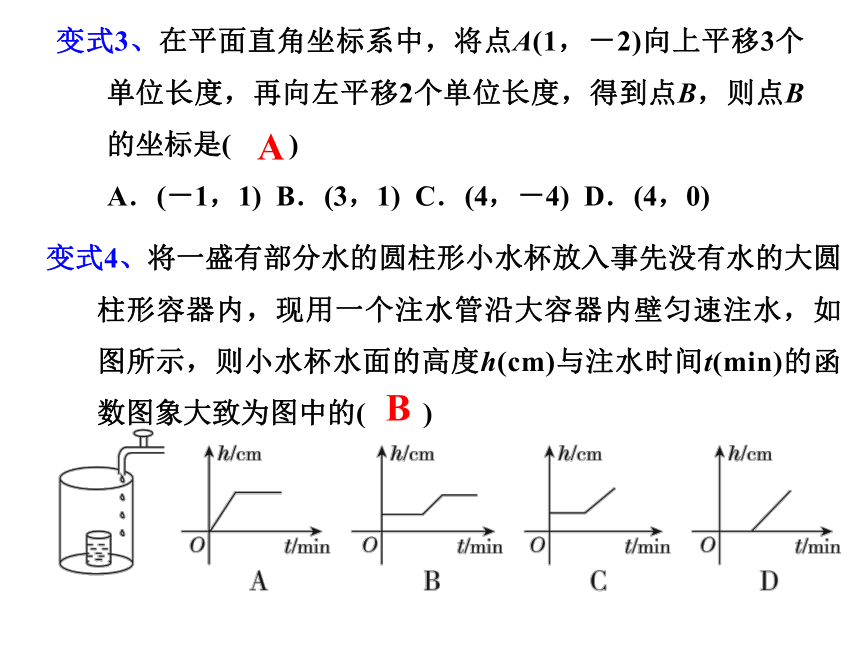
变式4、将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一个注水管沿大容器内壁匀速注水,如图所示,则小水杯水面的高度h(cm)与注水时间t(min)的函数图象大致为图中的( )
B
一次函数
一般地,如果y= k x+b (k、b是常数,k≠0),那么y叫做x的一次函数.
正比例函数
特别地,当b=____时,一次函数y=k x+b变为y= _____(k为常数,k≠0),这时y叫做x的正比例函数.
0
kx
二、一次函数
1.一次函数与正比例函数的概念
2.分段函数
当自变量的取值范围不同时,函数的解析式也不同,这样的函数称为分段函数.
例6.已知y=(m-3)x|m|-2+1是y关于x的一次函数,则m的值是( )
A.-3 B.3 C.±3 D.±2
B
A
变式5、已知y=(m+1)x2-|m|+n+4.
(1)当m,n为何值时,y是x的一次函数?并写出关系式.
(2)当m,n为何值时,y是x的正比例函数?并写出关系式.
解:(1)由题意知2-|m|=1,m+1≠0,
解得m=1,
即当m=1,n为任意实数时,y是x的一次函数,关系式为 :y=2x+n+4.
(2) 由题意知2-|m|=1,m+1≠0,n+4=0,
解得m=1,n=-4,
即当m=1,n=-4时,y是x的正比例函数,关系式为y=2x.
函数
字母系数取值
( k>0 )
图象
经过的象限
函数性质
y=kx+b
(k≠0)
b>0
y随x增大而
增大
b=0
b<0
第一、三象限
第一、二、三象限
第一、三、四象限
3.一次函数的图象与性质
函数
字母系数取值
( k<0 )
图象
经过的象限
函数性质
y=kx+b
(k≠0)
b>0
y随x增大而
减小
b=0
b<0
第一、二、
四象限
第二、四象限
第二、三、
四象限
D
例8、将直线y=-2x-1向上平移两个单位长度,平移后的直线所对应的函数关系式为( )
A.y=-2x-5 B.y=-2x-3
C.y=-2x+1 D.y=-2x+3
C
例10.一次函数y=5x-10的图象与x轴的交点坐标是____________,与y轴的交点坐标是________.
(2,0)
(0,-10)
例11、一次函数y=kx-k(k<0)的大致图象是( )
A
例12、已知一次函数y1=ax+b和y2=bx+a(a≠b),两个函数的
图象可能是( )
A
变式6.已知一次函数y=(2m+4)x+m-3,求:
(1)当m为何值时,y随x的增大而增大?
(2)当m为何值时,函数图象与y轴的交点在x轴下方?
(3)当m为何值时,函数图象经过原点?
(4)当m为何值时,这条直线平行于直线y=-x?
解:(1)2m+4>0,所以m>-2.
(2)m-3<0,且2m+4≠0,
∴ m<3,且m≠-2.
(3)m-3=0且2m+4≠0,
∴m=3.
求一次函数解析式的一般步骤:
(1)先设出函数解析式;
(2)根据条件列关于待定系数的方程(组);
(3)解方程(组)求出解析式中未知的系数;
(4)把求出的系数代入设的解析式,从而具体写出这个解析式.这种求解析式的方法叫待定系数法.
4.用待定系数法求一次函数的解析式
例13、如图,已知过点B(1,0)的直线l1与直线l2:y=2x+4
相交于点P(-1,a).
(1)求直线l1的表达式;
(2)求四边形PAOC的面积.
解:(1)∵点P(-1,a)在
直线l2:y=2x+4上,
∴2×(-1)+4=a,即a=2,则P点的坐标为(-1,2).
(2)∵直线l1与y轴相交于点C,
∴C点的坐标为(0,1),则OC=1.
又∵直线l2与x轴相交于点A,
∴A点的坐标为(-2,0),
∴OA=2.
求ax+b=0(a,b是
常数,a≠0)的解.
x为何值时,函数
y= ax+b的值为0?
从“数”的角度看
求ax+b=0(a, b是
常数,a≠0)的解.
求直线y= ax+b与
x 轴交点的横坐标.
从“形”的角度看
(1)一次函数与一元一次方程
5.一次函数与方程
一般地,任何一个二元一次方程都可以转化为一次函数y=kx+b(k、b为常数,且k≠0)的形式,所以每个二元一次方程都对应一个一次函数,也对应一条直线.
(2)一次函数与二元一次方程
方程的解 对应直线点的坐标.
A
x>3
1. 反比例函数的概念
定义:形如________ (k为常数,k≠0) 的函数称为反
比例函数,其中x是自变量,y是x的函数,k是比例
系数.
三种表示方法: 或 xy=k 或y=kx-1 (k≠0).
防错提醒:(1)k≠0;(2)自变量x≠0;(3)函数y≠0.
三、反比例函数
2. 反比例函数的图象和性质
(1) 反比例函数的图象:反比例函数 (k≠0)的
图象是 ,它既是轴对称图形又是中心
对称图形.
反比例函数的两条对称轴为直线 和 ;
对称中心是: .
双曲线
原点
y = x
y=-x
(2) 反比例函数的性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
图象
所在象限
性质
(k≠0)
k>0
第一、三象限(x,y同号)
在每个象限内,y 随 x 的增大而减小
k<0
第二、四象限(x,y异号)
在每个象限内,y 随 x 的增大而增大
x
y
o
x
y
o
(3) 反比例函数比例系数 k 的几何意义
k 的几何意义:反比例函数图象上的点 (x,y) 具有
两坐标之积 (xy=k) 为常数这一特点,即过双曲线
上任意一点,向两坐标轴作垂线,两条垂线与坐
标轴所围成的矩形的面积为常数 |k|.
规律:过双曲线上任意一点,向两坐标轴作垂线,
一条垂线与坐标轴、原点所围成的三角形的面积
为常数 .
3. 反比例函数的应用
?利用待定系数法确定反比例函数:
① 根据两变量之间的反比例关系,设 ;
② 代入图象上一个点的坐标,即 x、y 的一对
对应值,求出 k 的值;
③ 写出解析式.
例16、若y=(m-1)x|m|-2是反比例函数,则m的取值为( )
A.1 B.-1 C.±1 D.任意实数
B
C
4
(1)求一次函数与反比例函数的表达式
(2)请根据图象直接写出y1<y2时x的取值范围.
(2)根据图象可以看出y1<y2时x的取值范围为x<-2或0课堂小结
实际问题
函数
建立函
数模型
定义
自变量取值范围
表示法
一次函数
y=kx+b(k≠0)
应用
图象:一条直线
性质:
k>0,y 随x 的增大而增大
k<0,y 随x 的增大而减小
数形结合
一次函数与一次方程之间的关系
课堂小结
反比例函数
定义
图象
性质
x,y 的取值范围
增减性
对称性
k 的几何意义
应用
在实际生活中的应用
在物理学科中的应用
第17章 函数及其图象
要点梳理
1. 常量与变量
叫变量,
叫常量.
2.函数定义:
取值发生变化的量
取值固定不变的量
在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
一、函数
3.函数的图象:对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
列表法
解析法
图象法.
5.函数的三种表示方法:
4.描点法画图象的步骤:列表、描点、连线
例1.(1)设圆柱的底面半径R不变,圆柱的体积V与圆柱的高h的关系式是V=πR2h,在这个变化过程中常量和变量分别是什么?
(2)设圆柱的高h不变,在圆柱的体积V与圆柱的底面半径R的关系式V=πR2h中,常量和变量分别又是什么?
解:(1)常量是π和R,变量是V和h.
(2)常量是π和h,变量是V和R.
B
例3、已知点P(m+2,2m-4)在x轴上,则点P的坐标是( )
A.(4,0) B.(0,4)
C.(-4,0) D.(0,-4)
A
例4、点M(a,b)为平面直角坐标系中的点.
(1)当a>0,b<0时,点M位于第几象限?
(2)当ab>0时,点M位于第几象限?
(3)当a为任意非零实数,且b<0时,点M位于第几象限?
解:(1)第四象限.
(2)∵ab>0,
∴a>0且b>0或a<0且b<0.
∴点M位于第一象限或第三象限.
(3)第三象限或第四象限.
例5、已知点A(2,3)在函数y=ax2-x+1的图象上,则a等于( )
A.1 B.-1 C.2 D.-2
A
例6、如图,△ABC的边BC长是8,BC边上的高AD′是4,点D在BC上运动(不与C点重合),设BD长为x,则△ACD的面积y与x之间的函数关系式为_________________.
y=16-2x(0≤x<8)
D
变式2、若点(-m,3)与点(-5,n)关于y轴对称,则( )
A.m=-5,n=3
B.m=5,n=3
C.m=-5,n=-3
D.m=-3,n=5
A
变式3、在平面直角坐标系中,将点A(1,-2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,则点B的坐标是( )
A.(-1,1) B.(3,1) C.(4,-4) D.(4,0)
A
变式4、将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一个注水管沿大容器内壁匀速注水,如图所示,则小水杯水面的高度h(cm)与注水时间t(min)的函数图象大致为图中的( )
B
一次函数
一般地,如果y= k x+b (k、b是常数,k≠0),那么y叫做x的一次函数.
正比例函数
特别地,当b=____时,一次函数y=k x+b变为y= _____(k为常数,k≠0),这时y叫做x的正比例函数.
0
kx
二、一次函数
1.一次函数与正比例函数的概念
2.分段函数
当自变量的取值范围不同时,函数的解析式也不同,这样的函数称为分段函数.
例6.已知y=(m-3)x|m|-2+1是y关于x的一次函数,则m的值是( )
A.-3 B.3 C.±3 D.±2
B
A
变式5、已知y=(m+1)x2-|m|+n+4.
(1)当m,n为何值时,y是x的一次函数?并写出关系式.
(2)当m,n为何值时,y是x的正比例函数?并写出关系式.
解:(1)由题意知2-|m|=1,m+1≠0,
解得m=1,
即当m=1,n为任意实数时,y是x的一次函数,关系式为 :y=2x+n+4.
(2) 由题意知2-|m|=1,m+1≠0,n+4=0,
解得m=1,n=-4,
即当m=1,n=-4时,y是x的正比例函数,关系式为y=2x.
函数
字母系数取值
( k>0 )
图象
经过的象限
函数性质
y=kx+b
(k≠0)
b>0
y随x增大而
增大
b=0
b<0
第一、三象限
第一、二、三象限
第一、三、四象限
3.一次函数的图象与性质
函数
字母系数取值
( k<0 )
图象
经过的象限
函数性质
y=kx+b
(k≠0)
b>0
y随x增大而
减小
b=0
b<0
第一、二、
四象限
第二、四象限
第二、三、
四象限
D
例8、将直线y=-2x-1向上平移两个单位长度,平移后的直线所对应的函数关系式为( )
A.y=-2x-5 B.y=-2x-3
C.y=-2x+1 D.y=-2x+3
C
例10.一次函数y=5x-10的图象与x轴的交点坐标是____________,与y轴的交点坐标是________.
(2,0)
(0,-10)
例11、一次函数y=kx-k(k<0)的大致图象是( )
A
例12、已知一次函数y1=ax+b和y2=bx+a(a≠b),两个函数的
图象可能是( )
A
变式6.已知一次函数y=(2m+4)x+m-3,求:
(1)当m为何值时,y随x的增大而增大?
(2)当m为何值时,函数图象与y轴的交点在x轴下方?
(3)当m为何值时,函数图象经过原点?
(4)当m为何值时,这条直线平行于直线y=-x?
解:(1)2m+4>0,所以m>-2.
(2)m-3<0,且2m+4≠0,
∴ m<3,且m≠-2.
(3)m-3=0且2m+4≠0,
∴m=3.
求一次函数解析式的一般步骤:
(1)先设出函数解析式;
(2)根据条件列关于待定系数的方程(组);
(3)解方程(组)求出解析式中未知的系数;
(4)把求出的系数代入设的解析式,从而具体写出这个解析式.这种求解析式的方法叫待定系数法.
4.用待定系数法求一次函数的解析式
例13、如图,已知过点B(1,0)的直线l1与直线l2:y=2x+4
相交于点P(-1,a).
(1)求直线l1的表达式;
(2)求四边形PAOC的面积.
解:(1)∵点P(-1,a)在
直线l2:y=2x+4上,
∴2×(-1)+4=a,即a=2,则P点的坐标为(-1,2).
(2)∵直线l1与y轴相交于点C,
∴C点的坐标为(0,1),则OC=1.
又∵直线l2与x轴相交于点A,
∴A点的坐标为(-2,0),
∴OA=2.
求ax+b=0(a,b是
常数,a≠0)的解.
x为何值时,函数
y= ax+b的值为0?
从“数”的角度看
求ax+b=0(a, b是
常数,a≠0)的解.
求直线y= ax+b与
x 轴交点的横坐标.
从“形”的角度看
(1)一次函数与一元一次方程
5.一次函数与方程
一般地,任何一个二元一次方程都可以转化为一次函数y=kx+b(k、b为常数,且k≠0)的形式,所以每个二元一次方程都对应一个一次函数,也对应一条直线.
(2)一次函数与二元一次方程
方程的解 对应直线点的坐标.
A
x>3
1. 反比例函数的概念
定义:形如________ (k为常数,k≠0) 的函数称为反
比例函数,其中x是自变量,y是x的函数,k是比例
系数.
三种表示方法: 或 xy=k 或y=kx-1 (k≠0).
防错提醒:(1)k≠0;(2)自变量x≠0;(3)函数y≠0.
三、反比例函数
2. 反比例函数的图象和性质
(1) 反比例函数的图象:反比例函数 (k≠0)的
图象是 ,它既是轴对称图形又是中心
对称图形.
反比例函数的两条对称轴为直线 和 ;
对称中心是: .
双曲线
原点
y = x
y=-x
(2) 反比例函数的性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
图象
所在象限
性质
(k≠0)
k>0
第一、三象限(x,y同号)
在每个象限内,y 随 x 的增大而减小
k<0
第二、四象限(x,y异号)
在每个象限内,y 随 x 的增大而增大
x
y
o
x
y
o
(3) 反比例函数比例系数 k 的几何意义
k 的几何意义:反比例函数图象上的点 (x,y) 具有
两坐标之积 (xy=k) 为常数这一特点,即过双曲线
上任意一点,向两坐标轴作垂线,两条垂线与坐
标轴所围成的矩形的面积为常数 |k|.
规律:过双曲线上任意一点,向两坐标轴作垂线,
一条垂线与坐标轴、原点所围成的三角形的面积
为常数 .
3. 反比例函数的应用
?利用待定系数法确定反比例函数:
① 根据两变量之间的反比例关系,设 ;
② 代入图象上一个点的坐标,即 x、y 的一对
对应值,求出 k 的值;
③ 写出解析式.
例16、若y=(m-1)x|m|-2是反比例函数,则m的取值为( )
A.1 B.-1 C.±1 D.任意实数
B
C
4
(1)求一次函数与反比例函数的表达式
(2)请根据图象直接写出y1<y2时x的取值范围.
(2)根据图象可以看出y1<y2时x的取值范围为x<-2或0
实际问题
函数
建立函
数模型
定义
自变量取值范围
表示法
一次函数
y=kx+b(k≠0)
应用
图象:一条直线
性质:
k>0,y 随x 的增大而增大
k<0,y 随x 的增大而减小
数形结合
一次函数与一次方程之间的关系
课堂小结
反比例函数
定义
图象
性质
x,y 的取值范围
增减性
对称性
k 的几何意义
应用
在实际生活中的应用
在物理学科中的应用
