2020-2021学年华东师大版九年级下册27.1.6 圆周角——圆内接四边形课件(共20张)
文档属性
| 名称 | 2020-2021学年华东师大版九年级下册27.1.6 圆周角——圆内接四边形课件(共20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 448.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 11:18:58 | ||
图片预览




文档简介
第27章 圆
27.1 圆的认识
第6课时 圆周角——圆
内接四边形
1
课堂讲解
圆内接多边形
圆内接四边形对角互补
圆内接四边形外角等于内对角
2
课时流程
逐点
导讲练
课堂小结
作业提升
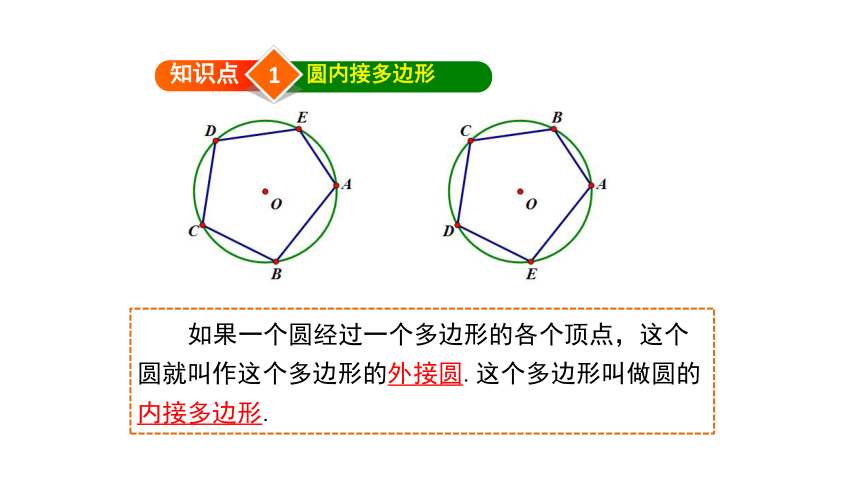
如果一个圆经过一个多边形的各个顶点,这个圆就叫作这个多边形的外接圆.这个多边形叫做圆的内接多边形.
1
知识点
圆内接多边形
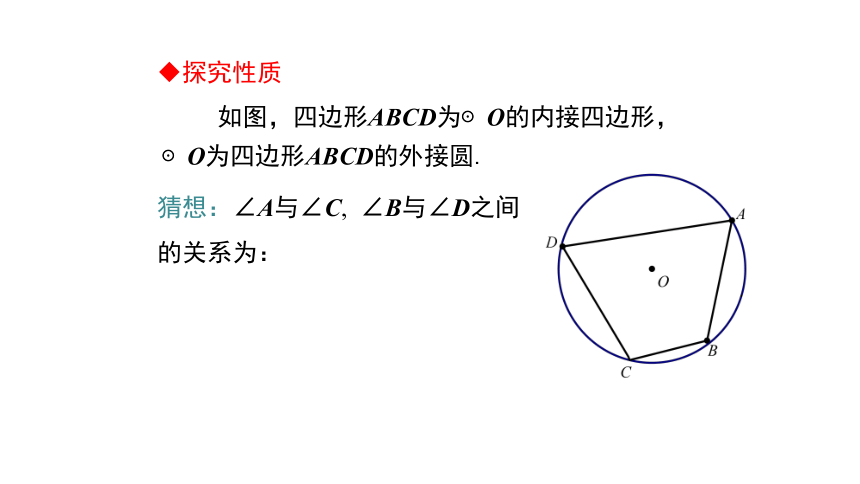
如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆.
探究性质
猜想:∠A与∠C, ∠B与∠D之间
的关系为:
2
知识点
圆内接四边形对角互补
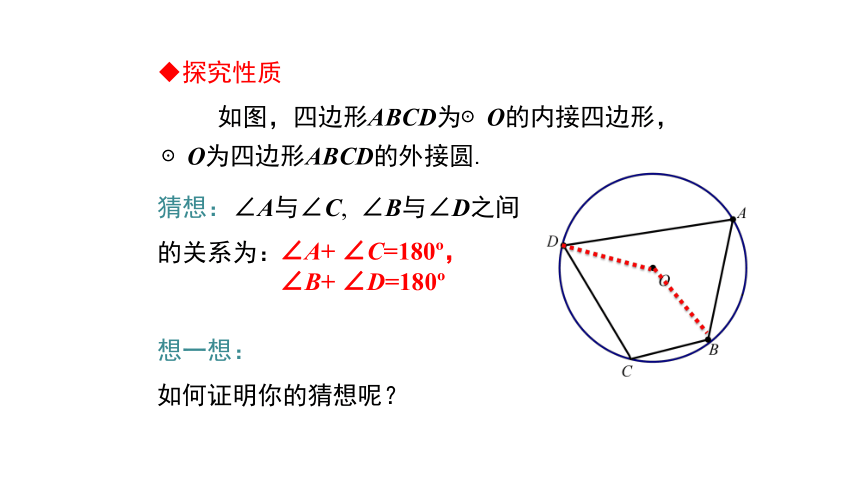
如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆.
探究性质
猜想:∠A与∠C, ∠B与∠D之间
的关系为:
∠A+ ∠C=180?,
∠B+ ∠D=180?
想一想:
如何证明你的猜想呢?
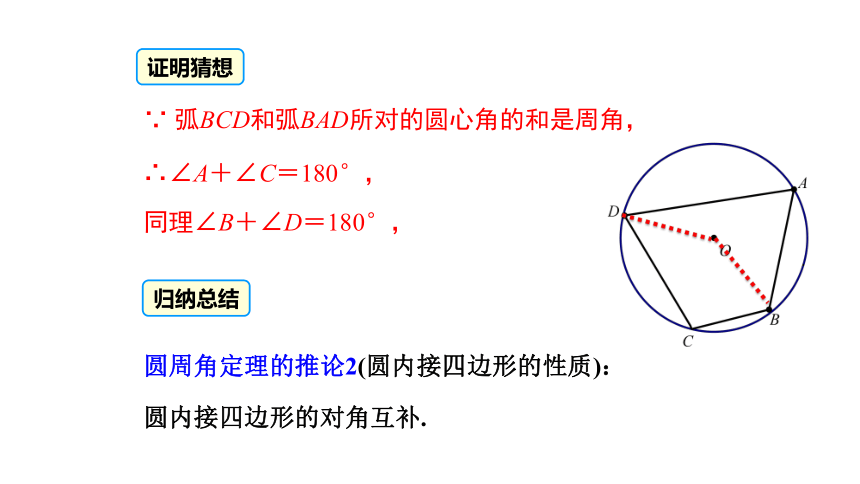
∵ 弧BCD和弧BAD所对的圆心角的和是周角,
∴∠A+∠C=180°,
同理∠B+∠D=180°,
证明猜想
归纳总结
圆周角定理的推论2(圆内接四边形的性质):
圆内接四边形的对角互补.
如图所示,四边形ABCD 为⊙ O 的内接四边形,已知∠ BOD=100°,则∠ BCD 的度数为( )
A. 50° B. 80° C. 100° D. 130°
例1
∵∠ BAD 与∠ BOD 是同弧所对的圆周角和圆
心角,∴∠ BAD = ∠ BOD = ×100°= 50°.
又∵四边形ABCD 为⊙ O 的内接四边形,
∴∠ BCD+ ∠ BAD = 180°.
∴∠ BCD = 180°- ∠ BAD = 180°-50°= 130°.
导引:
D
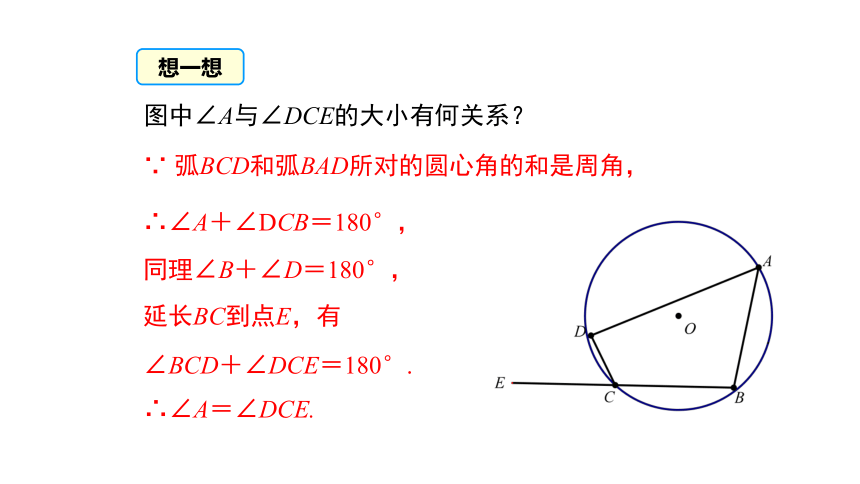
∵ 弧BCD和弧BAD所对的圆心角的和是周角,
∴∠A+∠DCB=180°,
同理∠B+∠D=180°,
延长BC到点E,有
∠BCD+∠DCE=180°.
∴∠A=∠DCE.
想一想
图中∠A与∠DCE的大小有何关系?
推论:圆的内接四边形的任何一个外角都等于它的内对角.
C
O
D
B
A
E
3
知识点
圆内接四边形外角等于内对角
已知:如图,两个等圆⊙O1和⊙O2相交于A,B两点,
经过点A的直线与两圆分别交于点C、点D,经过点B
的直线与两圆分别交于点E、点F.若CD∥EF,求证:
(1)四边形CEFD是平行四边形;
(2) .
例2
(1)连结AB,如图.
∵四边形ABEC是⊙O1的内接四边形,∴∠BAD=∠E.
又∵四边形ADFB是⊙O2的内接四边形,
∴∠BAD+∠F=180°,∴∠E+∠F=180°,
∴CE∥DF.
又∵CD∥EF,∴四边形CEFD是平行四边形.
(2)由(1)得:四边形CEFD是平行四边形,∴CE=DF.
又∵⊙O1和⊙O2是两个等圆,∴
解:
1.判断
(1)同一个圆中等弧所对的圆周角相等 ( )
(2)相等的弦所对的圆周角也相等 ( )
(3)同弦所对的圆周角相等 ( )
√
×
×
当堂训练
2.已知△ABC的三个顶点在⊙O上,∠BAC=50°,
∠ABC=47°, 则∠AOB= .
B
A
C
O
166°
3.如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为( )
A.30° B.40° C.50° D.60°
A
【规律方法】解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理.
A
B
C
D
O
4.如图,四边形ABCD内接于⊙O,如果∠BOD=130°,则∠BCD的度数是( )
A 115° B 130°
C 65° D 50°
5.如图,等边三角形ABC内接于⊙O,P是AB上的一点,则∠APB= .
A
B
C
P
C
120°
6.如图,已知圆心角∠AOB=100°,则圆周角
∠ACB= ,∠ADB= .
D
A
O
C
B
130°
50°
7.如图,△ABC的顶点A、B、C
都在⊙O上,∠C=30 °,AB=2,
则⊙O的半径是 .
C
A
B
O
解:连接OA、OB
∵∠C=30 ° ,∴∠AOB=60 °
又∵OA=OB ,∴△AOB是等边三角形
∴OA=OB=AB=2,即半径为2.
2
A
O
B
C
∴∠ACB=2∠BAC
证明:
8. 如图,OA,OB,OC都是⊙O的半径,∠AOB=
2∠BOC. 求证:∠ACB=2∠BAC.
∠AOB=2∠BOC,
9.船在航行过程中,船长通过测定角数来确定是否遇到暗礁,如图,A、B表示灯塔,暗礁分布在经过A、B两点的一个圆形区域内,优弧AB上任一点C都是有触礁危险的临界点,∠ACB就是“危险角”,当船位于安全区域时,∠α与“危险角”有怎样的大小关系?
解:当船位于安全区域时,即船位于暗礁区域外(即⊙O外) ,与两个灯塔的夹角∠α小于“危险角”.
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆周角定理的推论
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等.
1.90°的圆周角所对的弦是直径;
2.圆内接四边形的对角互补.
1.顶点在圆上,2.两边都与圆相交的角(二者必须同时具备)
圆周角与直
线的关系
半圆或直径所对的圆周角都相等,都等于90°(直角).
27.1 圆的认识
第6课时 圆周角——圆
内接四边形
1
课堂讲解
圆内接多边形
圆内接四边形对角互补
圆内接四边形外角等于内对角
2
课时流程
逐点
导讲练
课堂小结
作业提升
如果一个圆经过一个多边形的各个顶点,这个圆就叫作这个多边形的外接圆.这个多边形叫做圆的内接多边形.
1
知识点
圆内接多边形
如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆.
探究性质
猜想:∠A与∠C, ∠B与∠D之间
的关系为:
2
知识点
圆内接四边形对角互补
如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆.
探究性质
猜想:∠A与∠C, ∠B与∠D之间
的关系为:
∠A+ ∠C=180?,
∠B+ ∠D=180?
想一想:
如何证明你的猜想呢?
∵ 弧BCD和弧BAD所对的圆心角的和是周角,
∴∠A+∠C=180°,
同理∠B+∠D=180°,
证明猜想
归纳总结
圆周角定理的推论2(圆内接四边形的性质):
圆内接四边形的对角互补.
如图所示,四边形ABCD 为⊙ O 的内接四边形,已知∠ BOD=100°,则∠ BCD 的度数为( )
A. 50° B. 80° C. 100° D. 130°
例1
∵∠ BAD 与∠ BOD 是同弧所对的圆周角和圆
心角,∴∠ BAD = ∠ BOD = ×100°= 50°.
又∵四边形ABCD 为⊙ O 的内接四边形,
∴∠ BCD+ ∠ BAD = 180°.
∴∠ BCD = 180°- ∠ BAD = 180°-50°= 130°.
导引:
D
∵ 弧BCD和弧BAD所对的圆心角的和是周角,
∴∠A+∠DCB=180°,
同理∠B+∠D=180°,
延长BC到点E,有
∠BCD+∠DCE=180°.
∴∠A=∠DCE.
想一想
图中∠A与∠DCE的大小有何关系?
推论:圆的内接四边形的任何一个外角都等于它的内对角.
C
O
D
B
A
E
3
知识点
圆内接四边形外角等于内对角
已知:如图,两个等圆⊙O1和⊙O2相交于A,B两点,
经过点A的直线与两圆分别交于点C、点D,经过点B
的直线与两圆分别交于点E、点F.若CD∥EF,求证:
(1)四边形CEFD是平行四边形;
(2) .
例2
(1)连结AB,如图.
∵四边形ABEC是⊙O1的内接四边形,∴∠BAD=∠E.
又∵四边形ADFB是⊙O2的内接四边形,
∴∠BAD+∠F=180°,∴∠E+∠F=180°,
∴CE∥DF.
又∵CD∥EF,∴四边形CEFD是平行四边形.
(2)由(1)得:四边形CEFD是平行四边形,∴CE=DF.
又∵⊙O1和⊙O2是两个等圆,∴
解:
1.判断
(1)同一个圆中等弧所对的圆周角相等 ( )
(2)相等的弦所对的圆周角也相等 ( )
(3)同弦所对的圆周角相等 ( )
√
×
×
当堂训练
2.已知△ABC的三个顶点在⊙O上,∠BAC=50°,
∠ABC=47°, 则∠AOB= .
B
A
C
O
166°
3.如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为( )
A.30° B.40° C.50° D.60°
A
【规律方法】解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理.
A
B
C
D
O
4.如图,四边形ABCD内接于⊙O,如果∠BOD=130°,则∠BCD的度数是( )
A 115° B 130°
C 65° D 50°
5.如图,等边三角形ABC内接于⊙O,P是AB上的一点,则∠APB= .
A
B
C
P
C
120°
6.如图,已知圆心角∠AOB=100°,则圆周角
∠ACB= ,∠ADB= .
D
A
O
C
B
130°
50°
7.如图,△ABC的顶点A、B、C
都在⊙O上,∠C=30 °,AB=2,
则⊙O的半径是 .
C
A
B
O
解:连接OA、OB
∵∠C=30 ° ,∴∠AOB=60 °
又∵OA=OB ,∴△AOB是等边三角形
∴OA=OB=AB=2,即半径为2.
2
A
O
B
C
∴∠ACB=2∠BAC
证明:
8. 如图,OA,OB,OC都是⊙O的半径,∠AOB=
2∠BOC. 求证:∠ACB=2∠BAC.
∠AOB=2∠BOC,
9.船在航行过程中,船长通过测定角数来确定是否遇到暗礁,如图,A、B表示灯塔,暗礁分布在经过A、B两点的一个圆形区域内,优弧AB上任一点C都是有触礁危险的临界点,∠ACB就是“危险角”,当船位于安全区域时,∠α与“危险角”有怎样的大小关系?
解:当船位于安全区域时,即船位于暗礁区域外(即⊙O外) ,与两个灯塔的夹角∠α小于“危险角”.
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆周角定理的推论
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等.
1.90°的圆周角所对的弦是直径;
2.圆内接四边形的对角互补.
1.顶点在圆上,2.两边都与圆相交的角(二者必须同时具备)
圆周角与直
线的关系
半圆或直径所对的圆周角都相等,都等于90°(直角).
