2020-2021学年华东师大版七年级下册9.1 三角形第4课时 三角形的外角和课件(共15张)
文档属性
| 名称 | 2020-2021学年华东师大版七年级下册9.1 三角形第4课时 三角形的外角和课件(共15张) |  | |
| 格式 | pptx | ||
| 文件大小 | 113.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 16:45:16 | ||
图片预览



文档简介
9.1 三角形
第4课时 三角形的外
角和
第9章 多边形
1
知识点
三角形的外角定义
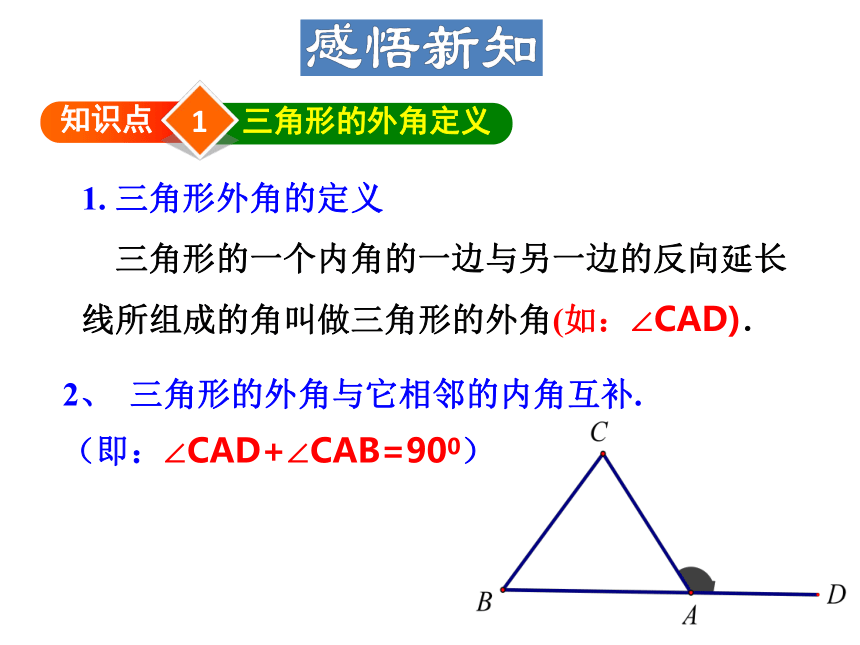
1. 三角形外角的定义
三角形的一个内角的一边与另一边的反向延长线所组成的角叫做三角形的外角(如:∠CAD).
2、 三角形的外角与它相邻的内角互补.
(即:∠CAD+∠CAB=900)
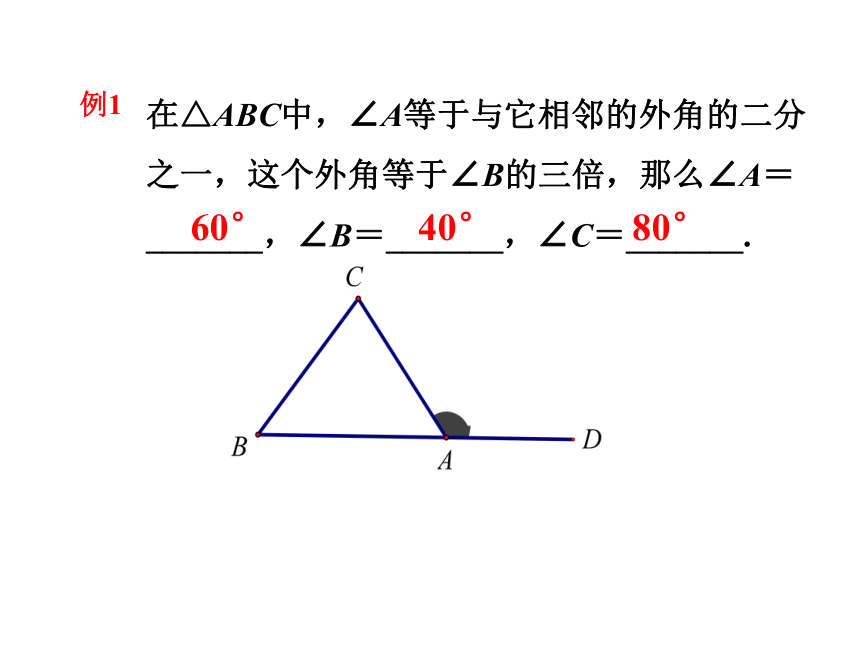
在△ABC中,∠A等于与它相邻的外角的二分之一,这个外角等于∠B的三倍,那么∠A=_______,∠B=_______,∠C=_______.
例1
60°
40°
80°
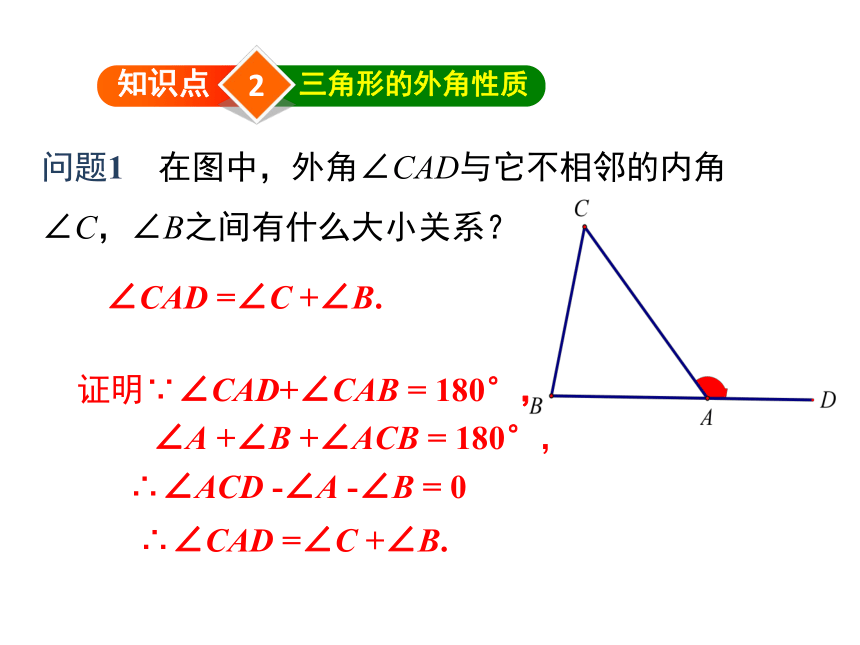
问题1 在图中,外角∠CAD与它不相邻的内角∠C,∠B之间有什么大小关系?
2
知识点
三角形的外角性质
证明∵∠CAD+∠CAB = 180°,
∠A +∠B +∠ACB = 180°,
∴∠ACD -∠A -∠B = 0
∴∠CAD =∠C +∠B.
∠CAD =∠C +∠B.
由此可知,三角形的外角有两条性质:
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于任何一个与它不相邻的内角.
如图,D是△ABC的BC于边上一点,∠B= ∠BAD, ∠ADC=70°, ∠BAC=80°. 求:
(1)∠B的度数;
(2)∠C的度数.
例2
(1)∵ ∠ADC是△ABD的外角(已知),
∴∠B+ ∠BAD =∠ADC=80° (三角形的一个外角等于与 它不相邻的两个内角的和).
又∵∠B= ∠BAD(已知),
∴∠B = 80°× = 40°(等量代换).
(2) ∵∠B+ ∠BAC +∠C = 180°(三角形的内角和等于180°),
∴∠C = 180°-∠B-∠BAC(等式的性质)
=180°-40°-70°=70°.
解:
3
知识点
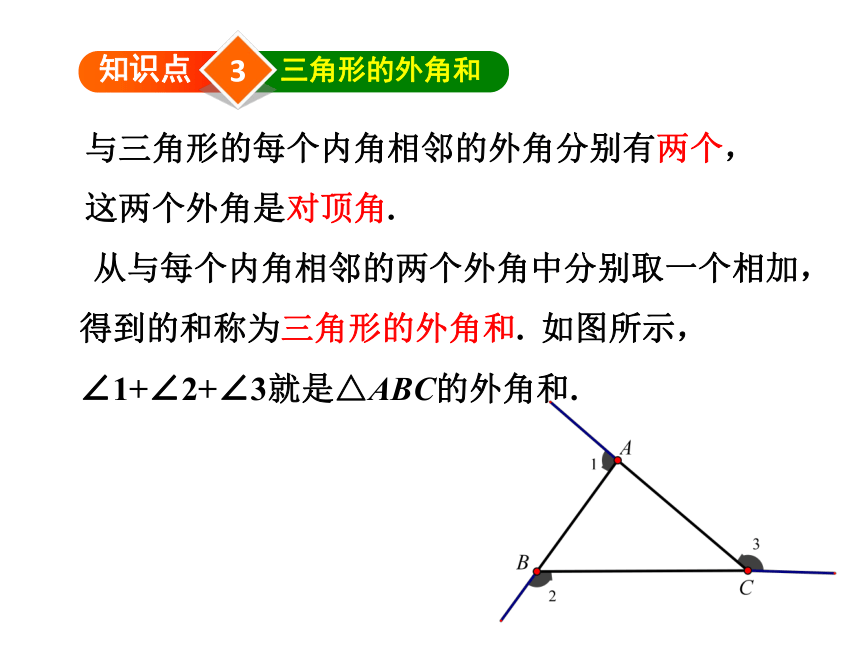
三角形的外角和
从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和. 如图所示,∠1+∠2+∠3就是△ABC的外角和.
与三角形的每个内角相邻的外角分别有两个,这两个外角是对顶角.
在图中, ∠1+______=180°,
∠2+______=180°,
∠3+______=180°.
三式相加可以得到
∠1+∠2+∠3+______+______+______=______. ①
而∠ACB +∠BAC +∠ABC= 180°, ②
将①与②相比较,你能得出什么结论?
∠BAC
∠CBA
∠ACB
∠BAC
∠CBA
∠ACB
3600
可以得到:
∠1+∠2+∠3= 360°.
由此可知:三角形的外角和等于360°.
要点精析:
三角形的外角和指的是三角形的每个顶点处
各取一个外角相加所得到的和,而不是指六个外
角的和.
如果三角形三个外角度数之比是1:2:3,则此三角形一定是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
例4
B
已知三角形的三个外角的度数比为2∶3∶4,则它的最大内角的度数为( )
A.90° B. 110°
C.100° D. 120°
例5
C
1.下列对三角形的外角和叙述正确的是( )
A.三角形的外角和等于180°
B.三角形的外角和就是所有外角的和
C.三角形的外角和等于所有外角和的一半
D.以上都不对
C
课堂练习
2.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.35° B.95°
C.85° D.75°
C
3.如图,∠A、∠1、∠2的大小关系是( )
A.∠A>∠1>∠2
B.∠2>∠1>∠A
C.∠A>∠2>∠1
D.∠2>∠A>∠1
B
定义
角一边必须是三角形的一边,另一边必须是三角形另一边的延长线
性质
三角形的一个外角等于与它不相邻的两个内角的和
三角形的外角和
三角形的外角和等于360 °
三角形的外角
第4课时 三角形的外
角和
第9章 多边形
1
知识点
三角形的外角定义
1. 三角形外角的定义
三角形的一个内角的一边与另一边的反向延长线所组成的角叫做三角形的外角(如:∠CAD).
2、 三角形的外角与它相邻的内角互补.
(即:∠CAD+∠CAB=900)
在△ABC中,∠A等于与它相邻的外角的二分之一,这个外角等于∠B的三倍,那么∠A=_______,∠B=_______,∠C=_______.
例1
60°
40°
80°
问题1 在图中,外角∠CAD与它不相邻的内角∠C,∠B之间有什么大小关系?
2
知识点
三角形的外角性质
证明∵∠CAD+∠CAB = 180°,
∠A +∠B +∠ACB = 180°,
∴∠ACD -∠A -∠B = 0
∴∠CAD =∠C +∠B.
∠CAD =∠C +∠B.
由此可知,三角形的外角有两条性质:
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于任何一个与它不相邻的内角.
如图,D是△ABC的BC于边上一点,∠B= ∠BAD, ∠ADC=70°, ∠BAC=80°. 求:
(1)∠B的度数;
(2)∠C的度数.
例2
(1)∵ ∠ADC是△ABD的外角(已知),
∴∠B+ ∠BAD =∠ADC=80° (三角形的一个外角等于与 它不相邻的两个内角的和).
又∵∠B= ∠BAD(已知),
∴∠B = 80°× = 40°(等量代换).
(2) ∵∠B+ ∠BAC +∠C = 180°(三角形的内角和等于180°),
∴∠C = 180°-∠B-∠BAC(等式的性质)
=180°-40°-70°=70°.
解:
3
知识点
三角形的外角和
从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和. 如图所示,∠1+∠2+∠3就是△ABC的外角和.
与三角形的每个内角相邻的外角分别有两个,这两个外角是对顶角.
在图中, ∠1+______=180°,
∠2+______=180°,
∠3+______=180°.
三式相加可以得到
∠1+∠2+∠3+______+______+______=______. ①
而∠ACB +∠BAC +∠ABC= 180°, ②
将①与②相比较,你能得出什么结论?
∠BAC
∠CBA
∠ACB
∠BAC
∠CBA
∠ACB
3600
可以得到:
∠1+∠2+∠3= 360°.
由此可知:三角形的外角和等于360°.
要点精析:
三角形的外角和指的是三角形的每个顶点处
各取一个外角相加所得到的和,而不是指六个外
角的和.
如果三角形三个外角度数之比是1:2:3,则此三角形一定是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
例4
B
已知三角形的三个外角的度数比为2∶3∶4,则它的最大内角的度数为( )
A.90° B. 110°
C.100° D. 120°
例5
C
1.下列对三角形的外角和叙述正确的是( )
A.三角形的外角和等于180°
B.三角形的外角和就是所有外角的和
C.三角形的外角和等于所有外角和的一半
D.以上都不对
C
课堂练习
2.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.35° B.95°
C.85° D.75°
C
3.如图,∠A、∠1、∠2的大小关系是( )
A.∠A>∠1>∠2
B.∠2>∠1>∠A
C.∠A>∠2>∠1
D.∠2>∠A>∠1
B
定义
角一边必须是三角形的一边,另一边必须是三角形另一边的延长线
性质
三角形的一个外角等于与它不相邻的两个内角的和
三角形的外角和
三角形的外角和等于360 °
三角形的外角
