2020-2021学年华东师大版七年级下册9.1.3 三角形的内角和课件(共14张)
文档属性
| 名称 | 2020-2021学年华东师大版七年级下册9.1.3 三角形的内角和课件(共14张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 289.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 00:00:00 | ||
图片预览






文档简介
9.1 三角形
第3课时 三角形的内
角和
第9章 多边形
观察与思考
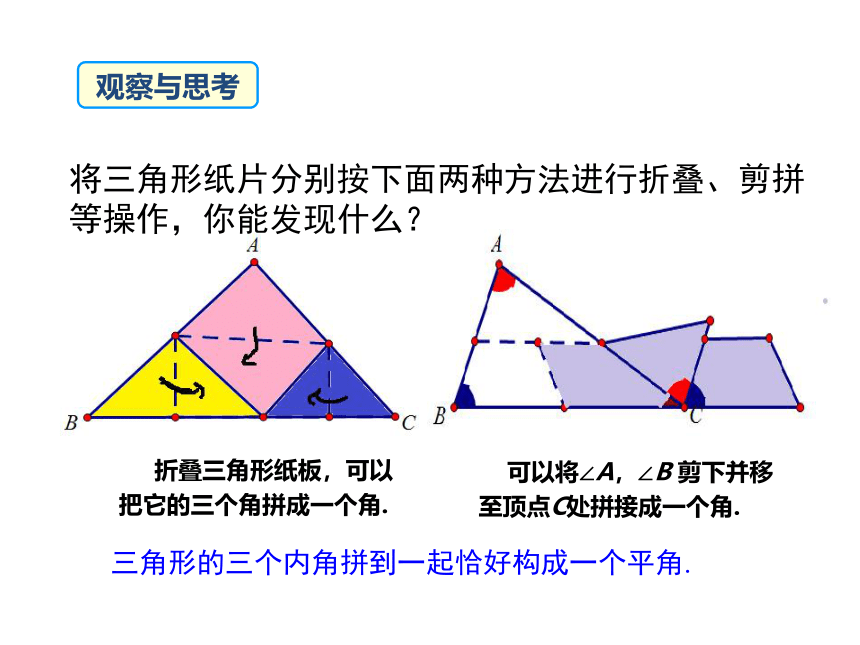
将三角形纸片分别按下面两种方法进行折叠、剪拼
等操作,你能发现什么?
折叠三角形纸板,可以把它的三个角拼成一个角.
可以将∠A,∠B 剪下并移至顶点C处拼接成一个角.
三角形的三个内角拼到一起恰好构成一个平角.
1
知识点
三角形的内角和性质
三角形内角和的推导方法:
证明:△ABC中,延长BC到
点D,过点画CM∥AB.
∴∠1=∠A,(两直线平行,内错角相等).
∠2=∠B, (两直线平行,同位角相等).
∵∠1+∠2+∠ACB=180°(平角定义).
∴∠A+∠B+∠ACB=180°(等量代换).
三角形三个内角的和等于180°
你还能想出其它的方法推出这个结论吗?
如图,△ABC中,∠A=46°,CE是∠ACB的平分线,B,C,D在同一条直线上,FD∥EC,∠D=42°,求∠B的度数.
例1
解:
∵FD∥EC,∴∠BCE=∠D=42°.
∵CE是∠ACB的平分线,
∴∠ACB=2∠BCE=84°.
∵∠A=46°,
∴∠B=180°-84°-46°=50°.
在△ABC中,∠A∶∠B∶∠C=2:3:4,则三角形各内角为多少度?
例2
解:
△ABC是直角三角形.理由如下:
∵∠A∶∠B∶∠C=2∶3:4,
∴可设∠A,∠B,∠C的度数分别为
2x°,3x°,4x°.
在△ABC中,∠A+∠B+∠C=180°
(三角形三个内角的和等于180°),
∴4x+2x+3x=180,解得x=20.
∴∠A=2x0=40° , ∠B=3x°=600,
∴∠C=4x°=80°,
∴△ABC是各内角分别为40° , 600,80°
2
知识点
直角三角形的两锐角性质
在△ABC 中,若∠C =90°,你能求出∠A,∠B 的度数吗?为什么?你能求出∠A +∠B 的度数吗?利用上面的结果,你能得出什么结论?
直角三角形的两个锐角互余.
应用格式:
在直角△ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =90°.
直角三角形可以用符号“Rt△”表示,直角三角形ABC 可以写成Rt△ABC
例3
如图,在△ABC中,AD是角平分线,∠B=50°,∠C=70°.
(1)求∠ADB的度数;
(2)若DE⊥AC于点E,求∠EDC的度数.
解:(1)∵∠B=50°,∠C=70°,
∴∠BAC=180°-∠B-∠C=60°.
又∵AD是角平分线,
∴∠BAD=30°,
∴∠ADB=180°-∠BAD-∠B=100°.
(2)∵DE⊥AC,
∴∠DEC=90°,
∴∠EDC=180°-∠DEC-∠C=20°.
如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与
∠DFE的平分线相交于
点P,说明:△EFP为
直角三角形.
例4
解:
∵AB∥CD,∴∠BEF+∠DFE=180°.
∵EP为∠BEF的平分线,FP为∠EFD的平分线,
∴∠PEF= ∠BEF,∠PFE= ∠DFE,
∴∠PEF+∠PFE= (∠BEF+∠DFE)= ×180°=90°
∴△EFP为直角三角形.
1.如图,在△ABC中,∠A=60°,∠B=40°,则∠C等于( )
A.100°
B.80°
C.60°
D.40°
B
课堂练习
2、一个三角形的三个内角的度数之比为1:2:3,则这个三角形一定是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
B
3、如图,在直角三角形ABC中,∠ACB=90°,CD⊥AB于D.图中有与∠A相等的角吗?为什么?
解:有.
理由:∵CD⊥AB,
∴∠B+∠BCD=90°.
∵∠ACB=90°,
∴∠B+∠A=90°.
∴∠BCD=∠A.
三角形的内角和等于180°.
直角三角形的两锐角互余
第3课时 三角形的内
角和
第9章 多边形
观察与思考
将三角形纸片分别按下面两种方法进行折叠、剪拼
等操作,你能发现什么?
折叠三角形纸板,可以把它的三个角拼成一个角.
可以将∠A,∠B 剪下并移至顶点C处拼接成一个角.
三角形的三个内角拼到一起恰好构成一个平角.
1
知识点
三角形的内角和性质
三角形内角和的推导方法:
证明:△ABC中,延长BC到
点D,过点画CM∥AB.
∴∠1=∠A,(两直线平行,内错角相等).
∠2=∠B, (两直线平行,同位角相等).
∵∠1+∠2+∠ACB=180°(平角定义).
∴∠A+∠B+∠ACB=180°(等量代换).
三角形三个内角的和等于180°
你还能想出其它的方法推出这个结论吗?
如图,△ABC中,∠A=46°,CE是∠ACB的平分线,B,C,D在同一条直线上,FD∥EC,∠D=42°,求∠B的度数.
例1
解:
∵FD∥EC,∴∠BCE=∠D=42°.
∵CE是∠ACB的平分线,
∴∠ACB=2∠BCE=84°.
∵∠A=46°,
∴∠B=180°-84°-46°=50°.
在△ABC中,∠A∶∠B∶∠C=2:3:4,则三角形各内角为多少度?
例2
解:
△ABC是直角三角形.理由如下:
∵∠A∶∠B∶∠C=2∶3:4,
∴可设∠A,∠B,∠C的度数分别为
2x°,3x°,4x°.
在△ABC中,∠A+∠B+∠C=180°
(三角形三个内角的和等于180°),
∴4x+2x+3x=180,解得x=20.
∴∠A=2x0=40° , ∠B=3x°=600,
∴∠C=4x°=80°,
∴△ABC是各内角分别为40° , 600,80°
2
知识点
直角三角形的两锐角性质
在△ABC 中,若∠C =90°,你能求出∠A,∠B 的度数吗?为什么?你能求出∠A +∠B 的度数吗?利用上面的结果,你能得出什么结论?
直角三角形的两个锐角互余.
应用格式:
在直角△ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =90°.
直角三角形可以用符号“Rt△”表示,直角三角形ABC 可以写成Rt△ABC
例3
如图,在△ABC中,AD是角平分线,∠B=50°,∠C=70°.
(1)求∠ADB的度数;
(2)若DE⊥AC于点E,求∠EDC的度数.
解:(1)∵∠B=50°,∠C=70°,
∴∠BAC=180°-∠B-∠C=60°.
又∵AD是角平分线,
∴∠BAD=30°,
∴∠ADB=180°-∠BAD-∠B=100°.
(2)∵DE⊥AC,
∴∠DEC=90°,
∴∠EDC=180°-∠DEC-∠C=20°.
如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与
∠DFE的平分线相交于
点P,说明:△EFP为
直角三角形.
例4
解:
∵AB∥CD,∴∠BEF+∠DFE=180°.
∵EP为∠BEF的平分线,FP为∠EFD的平分线,
∴∠PEF= ∠BEF,∠PFE= ∠DFE,
∴∠PEF+∠PFE= (∠BEF+∠DFE)= ×180°=90°
∴△EFP为直角三角形.
1.如图,在△ABC中,∠A=60°,∠B=40°,则∠C等于( )
A.100°
B.80°
C.60°
D.40°
B
课堂练习
2、一个三角形的三个内角的度数之比为1:2:3,则这个三角形一定是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
B
3、如图,在直角三角形ABC中,∠ACB=90°,CD⊥AB于D.图中有与∠A相等的角吗?为什么?
解:有.
理由:∵CD⊥AB,
∴∠B+∠BCD=90°.
∵∠ACB=90°,
∴∠B+∠A=90°.
∴∠BCD=∠A.
三角形的内角和等于180°.
直角三角形的两锐角互余
