2020-2021学年华东师大版七年级下册9.2.1 多边形课件(共16张)
文档属性
| 名称 | 2020-2021学年华东师大版七年级下册9.2.1 多边形课件(共16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 16:51:51 | ||
图片预览



文档简介
9.2 多边形的内角和与外角和
第1课时 多边形
第9章 多边形
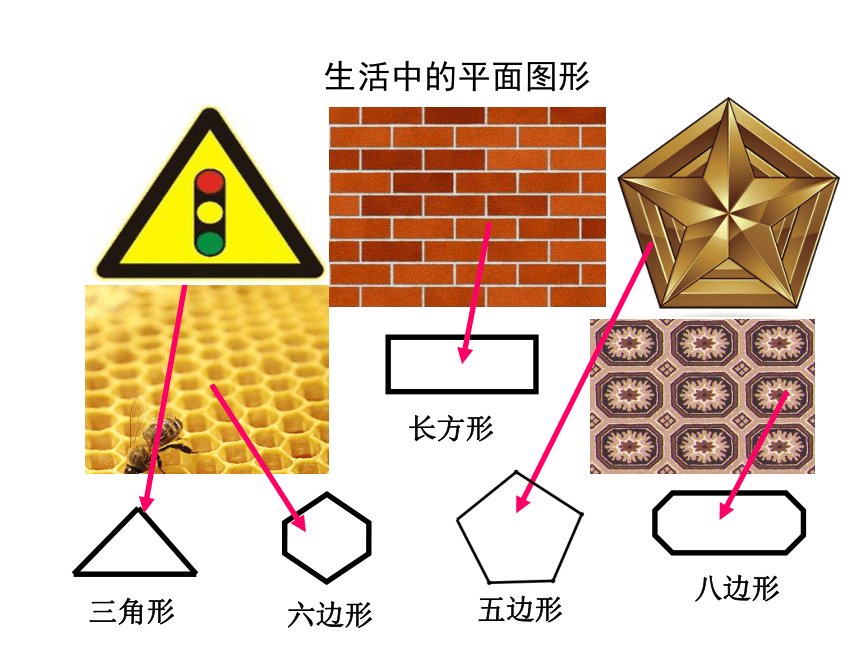
生活中的平面图形
三角形
长方形
五边形
六边形
八边形
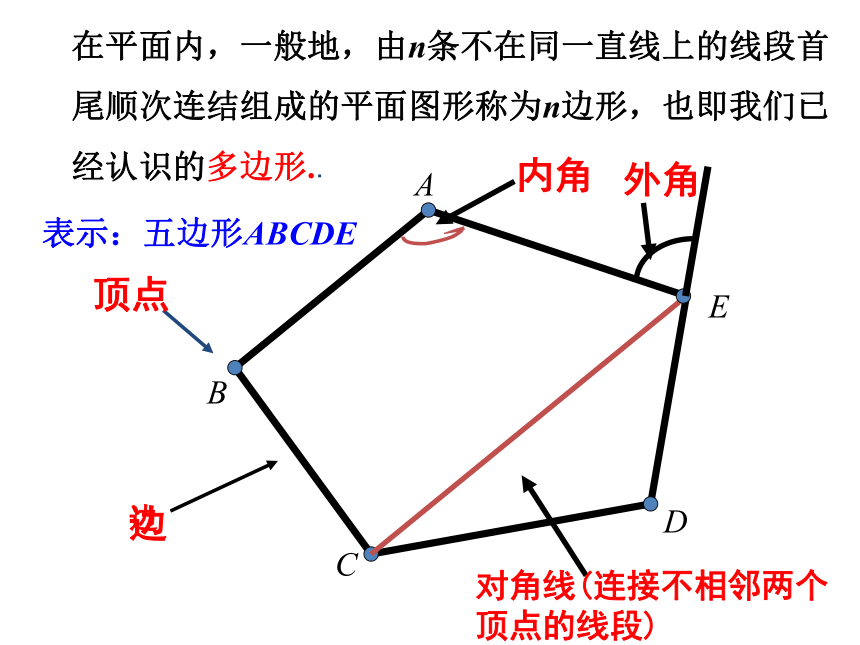
在平面内,一般地,由n条不在同一直线上的线段首尾顺次连结组成的平面图形称为n边形,也即我们已经认识的多边形..
顶点
内角
边
对角线(连接不相邻两个顶点的线段)
外角
表示:五边形ABCDE
A
C
B
D
E
边
n边形有____条边、___个顶点、___个内角和
_____外角;
n
n
n
2n
下列说法中,正确的有( )
(1)三角形是边数最少的多边形;
(2)由n条线段连结起来组成的图形叫做多边形;
(3)n边形有n条边、n个顶点、2n个内角和外角;
A.1个 B.2个 C.3个 D.4个
例1
A
2
知识点
多边形的对角线
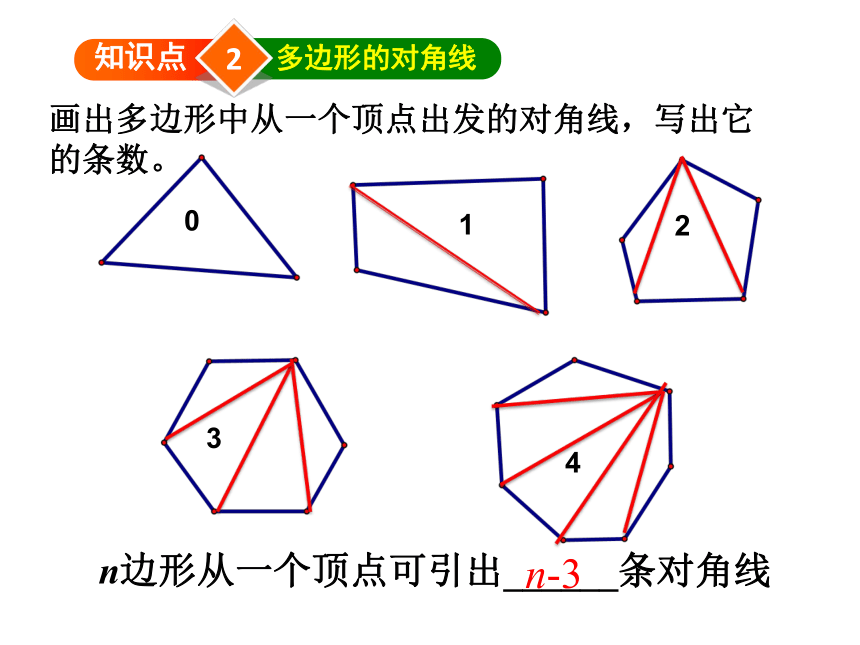
画出多边形中从一个顶点出发的对角线,写出它的条数。
0
1
2
3
4
n边形从一个顶点可引出______条对角线
n-3
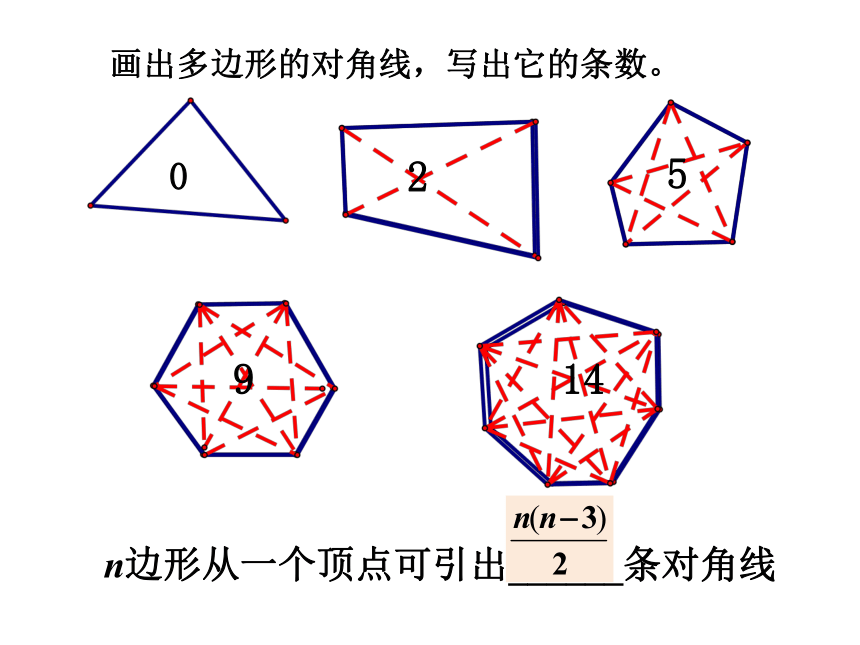
画出多边形的对角线,写出它的条数。
n边形从一个顶点可引出______条对角线
0
2
5
9
14
从n边形的一个顶点出发,可以引(n-3)条对角线,n边形的对角线条数为: .
若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是( )
A.十三边形 B.十二边形
C.十一边形 D.十边形
例2
导引:
如图,从n边形的一个顶点出发作对角线时,该
顶点本身及其相邻的两个顶点不能作,其余的
(n-3)个顶点每个顶点都与该顶点连成一条对
角线,故从n边形的一个顶点出发共引(n-3)
条对角线,所以n-3=10,所以n=13.
A
问题 观察下面多边形,它们的边、角有什么特点?
特点:
各边相等,各内角都相等的多边形.
2
知识点
正多边形
如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形(regular polygon).如正三角形、正四边形(正方形)、正五边形等.
下列说法:(1)等腰三角形是正多边形;(2)等边三角形是正多边形;(3)长方形是正多边形;(4)正方形是正多边形.其中正确的个数为( )
A. 1 B. 2
C. 3 D. 4
例2
B
1、下列图形中,属于多边形的是( )
A.线段 B.角
C.六边形 D.圆
课堂练习
C
2、过多边形的一个顶点可以引2 016条对角线,则这个多边形的边数是( )
A.2 016 B.2 017
C.2 018 D.2 019
D
3、下列属于正多边形的有( )
①等边三角形;②长方形;③正方形;
④梯形;⑤圆.
A.1个 B.2个
C.3个 D.4个
B
1. 正多边形概念
2、从n边形的一个顶点可以引(n-3)条对角线,一个n边形共有 条对角线.
3、正多边形
第1课时 多边形
第9章 多边形
生活中的平面图形
三角形
长方形
五边形
六边形
八边形
在平面内,一般地,由n条不在同一直线上的线段首尾顺次连结组成的平面图形称为n边形,也即我们已经认识的多边形..
顶点
内角
边
对角线(连接不相邻两个顶点的线段)
外角
表示:五边形ABCDE
A
C
B
D
E
边
n边形有____条边、___个顶点、___个内角和
_____外角;
n
n
n
2n
下列说法中,正确的有( )
(1)三角形是边数最少的多边形;
(2)由n条线段连结起来组成的图形叫做多边形;
(3)n边形有n条边、n个顶点、2n个内角和外角;
A.1个 B.2个 C.3个 D.4个
例1
A
2
知识点
多边形的对角线
画出多边形中从一个顶点出发的对角线,写出它的条数。
0
1
2
3
4
n边形从一个顶点可引出______条对角线
n-3
画出多边形的对角线,写出它的条数。
n边形从一个顶点可引出______条对角线
0
2
5
9
14
从n边形的一个顶点出发,可以引(n-3)条对角线,n边形的对角线条数为: .
若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是( )
A.十三边形 B.十二边形
C.十一边形 D.十边形
例2
导引:
如图,从n边形的一个顶点出发作对角线时,该
顶点本身及其相邻的两个顶点不能作,其余的
(n-3)个顶点每个顶点都与该顶点连成一条对
角线,故从n边形的一个顶点出发共引(n-3)
条对角线,所以n-3=10,所以n=13.
A
问题 观察下面多边形,它们的边、角有什么特点?
特点:
各边相等,各内角都相等的多边形.
2
知识点
正多边形
如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形(regular polygon).如正三角形、正四边形(正方形)、正五边形等.
下列说法:(1)等腰三角形是正多边形;(2)等边三角形是正多边形;(3)长方形是正多边形;(4)正方形是正多边形.其中正确的个数为( )
A. 1 B. 2
C. 3 D. 4
例2
B
1、下列图形中,属于多边形的是( )
A.线段 B.角
C.六边形 D.圆
课堂练习
C
2、过多边形的一个顶点可以引2 016条对角线,则这个多边形的边数是( )
A.2 016 B.2 017
C.2 018 D.2 019
D
3、下列属于正多边形的有( )
①等边三角形;②长方形;③正方形;
④梯形;⑤圆.
A.1个 B.2个
C.3个 D.4个
B
1. 正多边形概念
2、从n边形的一个顶点可以引(n-3)条对角线,一个n边形共有 条对角线.
3、正多边形
