2020-2021学年华东师大版七年级下册9.2.2 多边形的内角和与外角和 课件(共17张)
文档属性
| 名称 | 2020-2021学年华东师大版七年级下册9.2.2 多边形的内角和与外角和 课件(共17张) |  | |
| 格式 | pptx | ||
| 文件大小 | 145.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 16:55:55 | ||
图片预览





文档简介
9.2 多边形的内角和与外角和
第2课时 多边形的内角 和与外角和
1、三角形的内角和等于 ________
2、从n边形的一个顶点可以引________条对角线。
1800
(n-3)
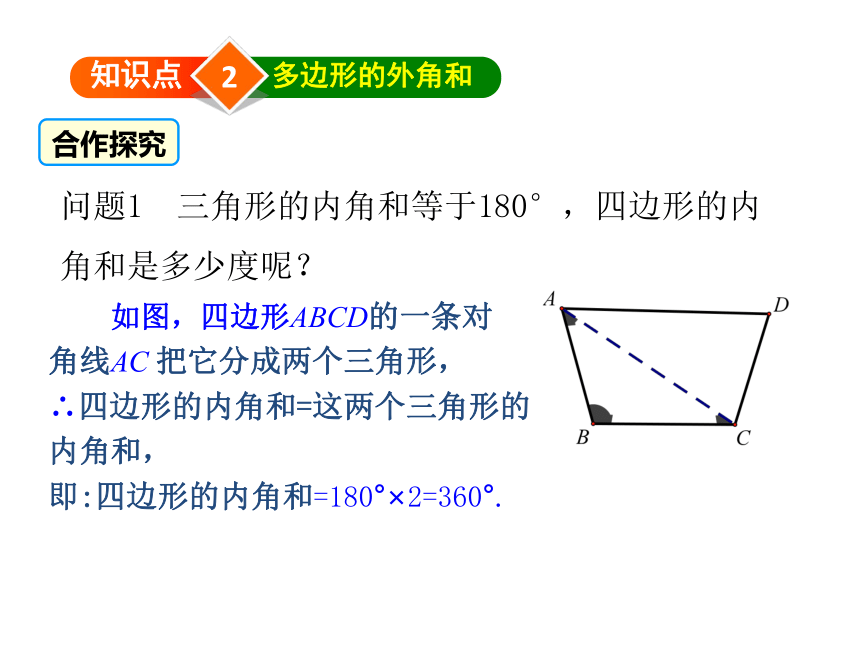
问题1 三角形的内角和等于180°,四边形的内角和是多少度呢?
合作探究
如图,四边形ABCD的一条对
角线AC 把它分成两个三角形,
∴四边形的内角和=这两个三角形的
内角和,
即:四边形的内角和=180°×2=360°.
2
知识点
多边形的外角和
{5940675A-B579-460E-94D1-54222C63F5DA}
五边形
5
5-3=2
5-2=3
(5-2) × 180°
六边形
6
七边形
7
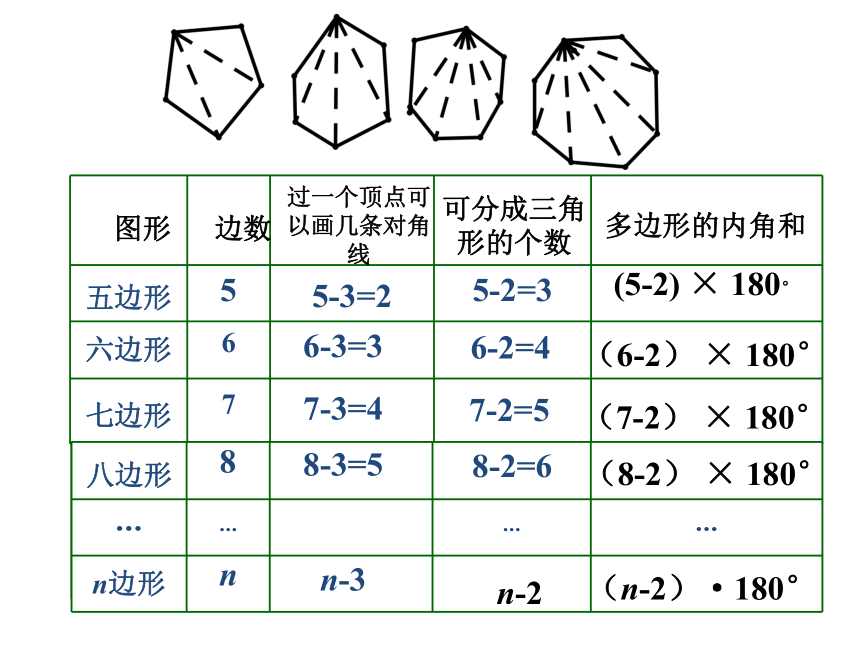
图形 边数
可分成三角形的个数
多边形的内角和
{5940675A-B579-460E-94D1-54222C63F5DA}
五边形
六边形
{5940675A-B579-460E-94D1-54222C63F5DA}
八边形
8
…
…
…
…
n边形
n
6-2=4
(6-2) × 180°
(7-2) × 180°
7-2=5
(8-2) × 180°
8-2=6
n-2
(n-2)·180°
过一个顶点可以画几条对角线
6-3=3
7-3=4
8-3=5
n-3
由此,我们得出
n边形的内角和为(n-2)·180°.
求八边形的内角和.
例1
解:
八边形的内角和为
(n-2)×180°=(8-2)×180°=1080°.
已知一个多边形的内角和等于2160°,求这个多边形的边数.
例2
解:
设这个多边形的边数为n,根据题意,得
(n-2)·180°= 2160°.
解得 n = 14.
即这个多边形的边数为14.
2
知识点
多边形的外角和
与多边形的每个内角相邻的外角分别有两个,这两个外角是对顶角.从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和.
问题 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和它相邻的内角有什么关系?
2.五个外角加上它们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和
有什么关系?
E
B
C
D
1
2
3
4
5
A
互补
900°
五个平角和(900°)-五边形的内角和(540°)=外角和(360°)
E
B
C
D
1
2
3
4
5
A
五边形外角和
=360 °
=5个平角
-五边形内角和
=5×180°
-(5-2) × 180°
结论:五边形的外角和等于360°.
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
-(n-2) · 180°
=360 °
=n个平角-n边形内角和
= n·180 °
E
B
C
D
1
2
3
4
n
A
任意多边形的外角和都为360°.
一个多边形的每个外角都是72°,这个多边形是几边形?
例3
解:
设多边形的边数为n,根据题意,得
n·72°=360°.
解得 n = 5.
因此,这个多边形是五边形.
一个多边形的内角和等于它外角和的5倍, 这个多边形是几边形?
例4
解:
设多边形的边数为n,根据题意,得
(n–2) ·180° = 5×360°.
解得 n = 12.
因此,这个多边形是十二边形.
课堂练习
1.如图,DA⊥AB,CD⊥DA,∠B=56°,则∠C的度数是( )
A.154° B.144°
C.134° D.124°
D
2、若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )
A.7 B.10
C.35 D.70
C
3.如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )
A.10 B.11
C.12 D.13
C
1、正n边形的内角和:
(n-2) ? 180 °(n ≥3的整数)
2、任意多边形的外角和都等于360°
特别注意:与边数无关。
第2课时 多边形的内角 和与外角和
1、三角形的内角和等于 ________
2、从n边形的一个顶点可以引________条对角线。
1800
(n-3)
问题1 三角形的内角和等于180°,四边形的内角和是多少度呢?
合作探究
如图,四边形ABCD的一条对
角线AC 把它分成两个三角形,
∴四边形的内角和=这两个三角形的
内角和,
即:四边形的内角和=180°×2=360°.
2
知识点
多边形的外角和
{5940675A-B579-460E-94D1-54222C63F5DA}
五边形
5
5-3=2
5-2=3
(5-2) × 180°
六边形
6
七边形
7
图形 边数
可分成三角形的个数
多边形的内角和
{5940675A-B579-460E-94D1-54222C63F5DA}
五边形
六边形
{5940675A-B579-460E-94D1-54222C63F5DA}
八边形
8
…
…
…
…
n边形
n
6-2=4
(6-2) × 180°
(7-2) × 180°
7-2=5
(8-2) × 180°
8-2=6
n-2
(n-2)·180°
过一个顶点可以画几条对角线
6-3=3
7-3=4
8-3=5
n-3
由此,我们得出
n边形的内角和为(n-2)·180°.
求八边形的内角和.
例1
解:
八边形的内角和为
(n-2)×180°=(8-2)×180°=1080°.
已知一个多边形的内角和等于2160°,求这个多边形的边数.
例2
解:
设这个多边形的边数为n,根据题意,得
(n-2)·180°= 2160°.
解得 n = 14.
即这个多边形的边数为14.
2
知识点
多边形的外角和
与多边形的每个内角相邻的外角分别有两个,这两个外角是对顶角.从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和.
问题 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和它相邻的内角有什么关系?
2.五个外角加上它们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和
有什么关系?
E
B
C
D
1
2
3
4
5
A
互补
900°
五个平角和(900°)-五边形的内角和(540°)=外角和(360°)
E
B
C
D
1
2
3
4
5
A
五边形外角和
=360 °
=5个平角
-五边形内角和
=5×180°
-(5-2) × 180°
结论:五边形的外角和等于360°.
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
-(n-2) · 180°
=360 °
=n个平角-n边形内角和
= n·180 °
E
B
C
D
1
2
3
4
n
A
任意多边形的外角和都为360°.
一个多边形的每个外角都是72°,这个多边形是几边形?
例3
解:
设多边形的边数为n,根据题意,得
n·72°=360°.
解得 n = 5.
因此,这个多边形是五边形.
一个多边形的内角和等于它外角和的5倍, 这个多边形是几边形?
例4
解:
设多边形的边数为n,根据题意,得
(n–2) ·180° = 5×360°.
解得 n = 12.
因此,这个多边形是十二边形.
课堂练习
1.如图,DA⊥AB,CD⊥DA,∠B=56°,则∠C的度数是( )
A.154° B.144°
C.134° D.124°
D
2、若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )
A.7 B.10
C.35 D.70
C
3.如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )
A.10 B.11
C.12 D.13
C
1、正n边形的内角和:
(n-2) ? 180 °(n ≥3的整数)
2、任意多边形的外角和都等于360°
特别注意:与边数无关。
