2020-2021学年华东师大版七年级下册10.3.2 旋转的特征课件(共16张)
文档属性
| 名称 | 2020-2021学年华东师大版七年级下册10.3.2 旋转的特征课件(共16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 348.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 00:00:00 | ||
图片预览





文档简介
10.3 旋转
第2课时 旋转的特征
第10章 轴对称、平移与旋转
复习引入
如图,将△ABC绕点C逆时针方向旋转,请说出:
旋转中心是点____;
点B的对应点是点____;
CA的对应边是______;
∠A的对应角是_______;
点A的旋转角是∠_______,
点B的旋转角是∠_______.
C
E
CD
∠D
ACD
BCE
思考:这些对应点、线段与角之间有什么关系呢?
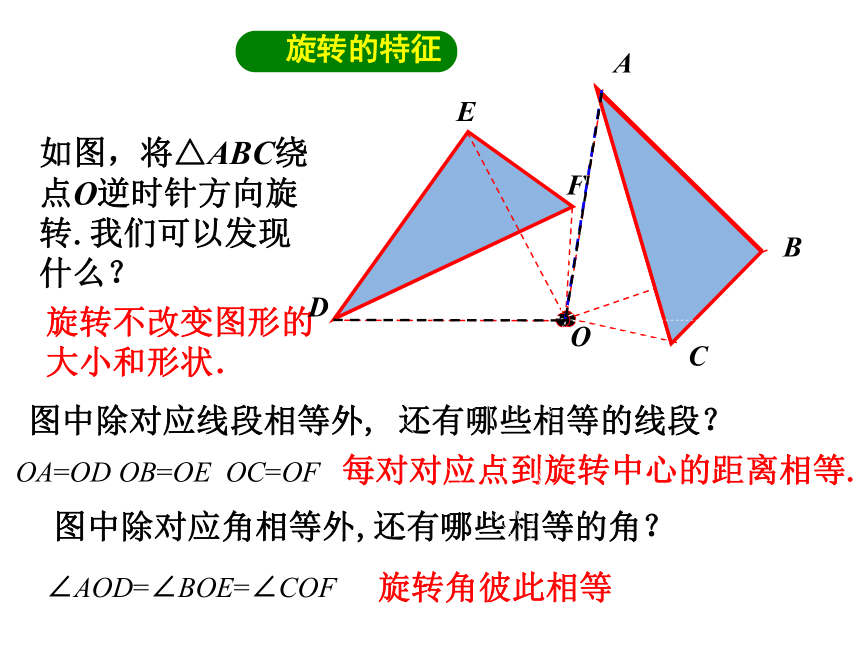
如图,将△ABC绕点O逆时针方向旋转.我们可以发现什么?
图中除对应线段相等外, 还有哪些相等的线段?
OA=OD OB=OE OC=OF
每对对应点到旋转中心的距离相等.
图中除对应角相等外,还有哪些相等的角?
∠AOD=∠BOE=∠COF
旋转角彼此相等
旋转不改变图形的
大小和形状.
D
E
A
B
F
C
O
旋转的特征
我们可以看到,在图1中,线段OA、OB都是绕点O逆时针旋转45°到对应线段OA′、OB′,而且OA = OA',OB = OB',AB = A′B′;
∠AOB = ∠A′OB′ ,∠A=∠A′,B=∠B′ .
在图2中,旋转中心是点O,点A、B、C都是绕点O逆时针旋转60°到对应点A′、B′、C′,而且OA =_____,OB =_____,OC =_____;
AB =_____,BC =_____,CA =_____;
∠CAB =_____,∠ABC =_____,∠BCA =_____.
图1
图2
旋转的特征:图形中每一点都绕着旋转中心按同一方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状与大小不变.
分析旋转形成的方法:“三个一”,即分析一个中心,一个方向,一个角度.
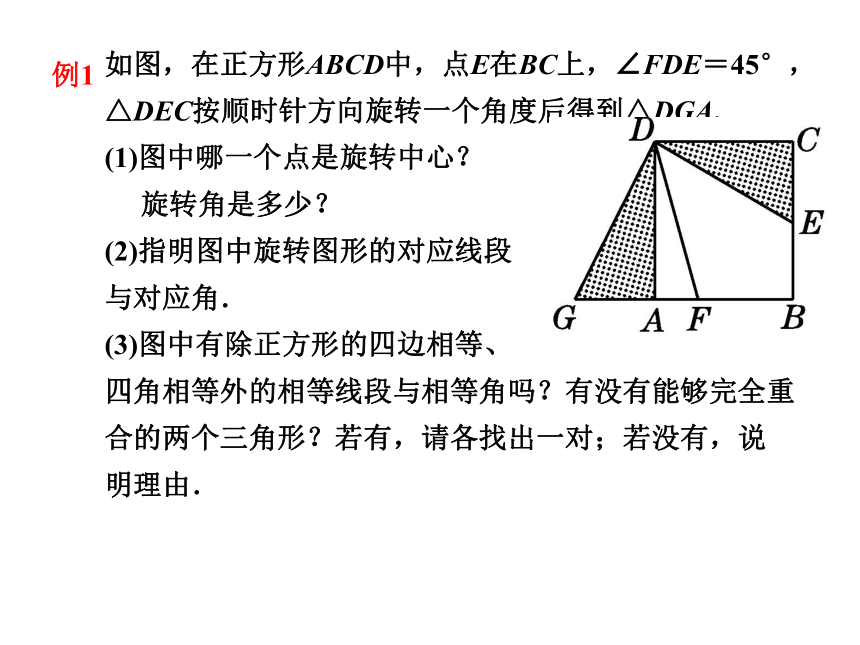
如图,在正方形ABCD中,点E在BC上,∠FDE=45°,△DEC按顺时针方向旋转一个角度后得到△DGA.
(1)图中哪一个点是旋转中心?
旋转角是多少?
(2)指明图中旋转图形的对应线段
与对应角.
(3)图中有除正方形的四边相等、
四角相等外的相等线段与相等角吗?有没有能够完全重合的两个三角形?若有,请各找出一对;若没有,说 明理由.
例1
解:
根据图形旋转的特征可以得到:
(1)图中△DEC是绕D点顺时针旋转90°后到达
△DGA位置的,所以点D为旋转中心,旋转角
是90°.
(2)图中DE与DG、DC与DA、EC与GA是对应线段,
∠CDE与∠ADG、∠C与∠DAG、∠DEC与∠G
是对应角.
(3)(答案不唯一)相等线段有:DG=DE等;
(答案不唯一)相等角有:∠G=∠DEC等;
能够完全重合的两个三角形是△DCE与△DAG.
同学们曾玩过万花筒,它是由三块等长的玻璃片围成的.如图是在万花筒中看到的一个图案.图中所有小三角形是大小相同的等边三角形,其中的四边形AEFG可以看成是把四边形ABCD以A为旋转中心( )
A.顺时针旋转60°得到
B.顺时针旋转120°得到
C.逆时针旋转60°得到
D.逆时针旋转120°得到
例2
B
旋转作图
1. 作一个图形的旋转图形的依据是旋转的性质:对应
点到旋转中心的距离相等,每组对应点都旋转相同
的角度.
2. 简单旋转作图的一般步骤:
(1)找出图形的关键点;
(2)确定旋转中心,旋转方向和旋转角;
(3)将关键点与旋转中心连结起来,然后按旋转方向
分别将它们旋转一个角,得到关键点的对应点;
(4)按照原图形的顺序连结这些对应点,所得到的图
形就是旋转后的图形.
3. 画旋转图形时,已知条件必须满足以下几点:
(1)基本图形;
(2)旋转中心;
(3)旋转角;
(4)旋转方向.
如图,△ABC绕点O旋转,使点A旋转到点D处,画出顺时针旋转后的三角形,并写出简要作法.
例3
解:
作法:(1)连结OA,OB,OC,OD;
(2)分别以OB,OC为边作∠BOM
=∠CON=∠AOD;
(3)分别在OM,ON上截取OE=OB,OF=OC;
(4)顺次连结DE,EF,FD.
△DEF就是所求作的三角形,如图所示.
拓展提升
①相同:都是一种运动;运动前后不改变图形的形状和大小.
B
A
C
O
②不同
图形变换
运动方向
运动量的衡量
平移
直线
移动一定距离
旋转
顺时针或逆时针
转动一定的角度
平移和旋转的异同:
1. 已知正方形ABCD中,E是BA延长线上的点,现将△ADE绕点A顺时针方向旋转到△ABP的位置.
(1)旋转了多少度?
(2)若连接EP,试分析 △AEP的形状.
A
B
C
D
E
P
90°
等腰直角三角形
课堂练习
A
B
C
D
E
2.如图,将Rt△ABC绕点A按顺时针方向旋转一定角度得Rt △ADE,点B的对应点D恰好落在BC边上.若AC= , ∠B=60 °,则CD的长为( )
A. 0.5 B. 1.5 C. D. 1
D
旋转的特征:图形中每一点都绕着旋转中心按同一方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状与大小不变.
分析旋转形成的方法:“三个一”,即分析一个中心,一个方向,一个角度.
第2课时 旋转的特征
第10章 轴对称、平移与旋转
复习引入
如图,将△ABC绕点C逆时针方向旋转,请说出:
旋转中心是点____;
点B的对应点是点____;
CA的对应边是______;
∠A的对应角是_______;
点A的旋转角是∠_______,
点B的旋转角是∠_______.
C
E
CD
∠D
ACD
BCE
思考:这些对应点、线段与角之间有什么关系呢?
如图,将△ABC绕点O逆时针方向旋转.我们可以发现什么?
图中除对应线段相等外, 还有哪些相等的线段?
OA=OD OB=OE OC=OF
每对对应点到旋转中心的距离相等.
图中除对应角相等外,还有哪些相等的角?
∠AOD=∠BOE=∠COF
旋转角彼此相等
旋转不改变图形的
大小和形状.
D
E
A
B
F
C
O
旋转的特征
我们可以看到,在图1中,线段OA、OB都是绕点O逆时针旋转45°到对应线段OA′、OB′,而且OA = OA',OB = OB',AB = A′B′;
∠AOB = ∠A′OB′ ,∠A=∠A′,B=∠B′ .
在图2中,旋转中心是点O,点A、B、C都是绕点O逆时针旋转60°到对应点A′、B′、C′,而且OA =_____,OB =_____,OC =_____;
AB =_____,BC =_____,CA =_____;
∠CAB =_____,∠ABC =_____,∠BCA =_____.
图1
图2
旋转的特征:图形中每一点都绕着旋转中心按同一方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状与大小不变.
分析旋转形成的方法:“三个一”,即分析一个中心,一个方向,一个角度.
如图,在正方形ABCD中,点E在BC上,∠FDE=45°,△DEC按顺时针方向旋转一个角度后得到△DGA.
(1)图中哪一个点是旋转中心?
旋转角是多少?
(2)指明图中旋转图形的对应线段
与对应角.
(3)图中有除正方形的四边相等、
四角相等外的相等线段与相等角吗?有没有能够完全重合的两个三角形?若有,请各找出一对;若没有,说 明理由.
例1
解:
根据图形旋转的特征可以得到:
(1)图中△DEC是绕D点顺时针旋转90°后到达
△DGA位置的,所以点D为旋转中心,旋转角
是90°.
(2)图中DE与DG、DC与DA、EC与GA是对应线段,
∠CDE与∠ADG、∠C与∠DAG、∠DEC与∠G
是对应角.
(3)(答案不唯一)相等线段有:DG=DE等;
(答案不唯一)相等角有:∠G=∠DEC等;
能够完全重合的两个三角形是△DCE与△DAG.
同学们曾玩过万花筒,它是由三块等长的玻璃片围成的.如图是在万花筒中看到的一个图案.图中所有小三角形是大小相同的等边三角形,其中的四边形AEFG可以看成是把四边形ABCD以A为旋转中心( )
A.顺时针旋转60°得到
B.顺时针旋转120°得到
C.逆时针旋转60°得到
D.逆时针旋转120°得到
例2
B
旋转作图
1. 作一个图形的旋转图形的依据是旋转的性质:对应
点到旋转中心的距离相等,每组对应点都旋转相同
的角度.
2. 简单旋转作图的一般步骤:
(1)找出图形的关键点;
(2)确定旋转中心,旋转方向和旋转角;
(3)将关键点与旋转中心连结起来,然后按旋转方向
分别将它们旋转一个角,得到关键点的对应点;
(4)按照原图形的顺序连结这些对应点,所得到的图
形就是旋转后的图形.
3. 画旋转图形时,已知条件必须满足以下几点:
(1)基本图形;
(2)旋转中心;
(3)旋转角;
(4)旋转方向.
如图,△ABC绕点O旋转,使点A旋转到点D处,画出顺时针旋转后的三角形,并写出简要作法.
例3
解:
作法:(1)连结OA,OB,OC,OD;
(2)分别以OB,OC为边作∠BOM
=∠CON=∠AOD;
(3)分别在OM,ON上截取OE=OB,OF=OC;
(4)顺次连结DE,EF,FD.
△DEF就是所求作的三角形,如图所示.
拓展提升
①相同:都是一种运动;运动前后不改变图形的形状和大小.
B
A
C
O
②不同
图形变换
运动方向
运动量的衡量
平移
直线
移动一定距离
旋转
顺时针或逆时针
转动一定的角度
平移和旋转的异同:
1. 已知正方形ABCD中,E是BA延长线上的点,现将△ADE绕点A顺时针方向旋转到△ABP的位置.
(1)旋转了多少度?
(2)若连接EP,试分析 △AEP的形状.
A
B
C
D
E
P
90°
等腰直角三角形
课堂练习
A
B
C
D
E
2.如图,将Rt△ABC绕点A按顺时针方向旋转一定角度得Rt △ADE,点B的对应点D恰好落在BC边上.若AC= , ∠B=60 °,则CD的长为( )
A. 0.5 B. 1.5 C. D. 1
D
旋转的特征:图形中每一点都绕着旋转中心按同一方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状与大小不变.
分析旋转形成的方法:“三个一”,即分析一个中心,一个方向,一个角度.
