2020-2021学年华东师大版八年级下册第20章 数据的整理与初步处理 小结与复习课件(共22张)
文档属性
| 名称 | 2020-2021学年华东师大版八年级下册第20章 数据的整理与初步处理 小结与复习课件(共22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 370.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 17:42:11 | ||
图片预览







文档简介
小结与复习
第20章 数据的整理与初步处理
要点梳理
一、数据的集中趋势
平均数
定义
一组数据的平均值称为这组数据的平均数
算术平
均数
一般地,如果有n个数x1,x2,…,xn,那么_____________________叫做这n个数的平均数.
加权平
均数
一般地,若n个数x1,x2,…,xn的权分别
是w1,w2,…,wn,则
___________________
叫做这n个数的加权平均数.
最多
中间位置的数
两个数据的平均数
中位数
定义
将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于________________就是这组数据的中位数,如果数据的个数是偶数,则中间_________________________就是这组数据的中位数
防错
提醒
确定中位数时,一定要注意先把整组数据按照大小顺序排列,再确定
众
数
定义
一组数据中出现次数________的数据叫做这组数据的众数
防错
提醒
(1)一组数据中众数不一定只有一个;(2)当一组数据中出现异常值时,其平均数往往不能正确反映这组数据的集中趋势,就应考虑用中位数或众数来分析
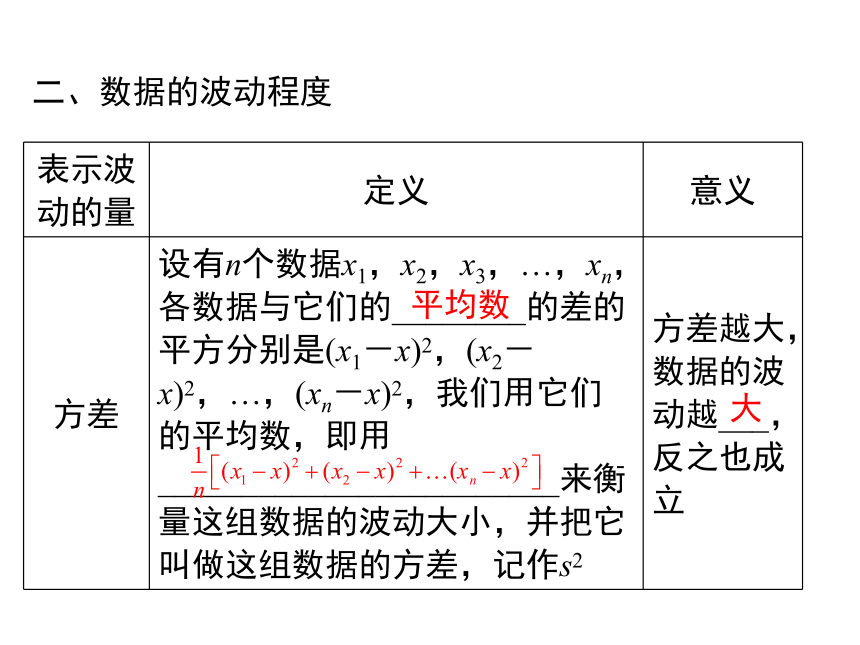
二、数据的波动程度
平均数
大
表示波
动的量
定义
意义
方差
设有n个数据x1,x2,x3,…,xn,各数据与它们的________的差的平方分别是(x1-x)2,(x2-x)2,…,(xn-x)2,我们用它们的平均数,即用________________________来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作s2
方差越大,数据的波动越___,反之也成立
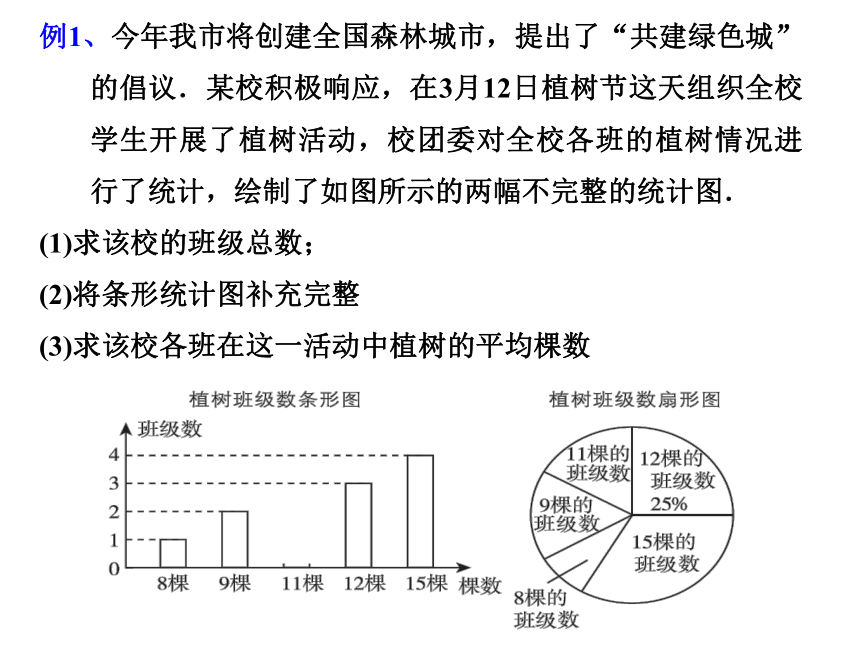
例1、今年我市将创建全国森林城市,提出了“共建绿色城”的倡议.某校积极响应,在3月12日植树节这天组织全校学生开展了植树活动,校团委对全校各班的植树情况进行了统计,绘制了如图所示的两幅不完整的统计图.
(1)求该校的班级总数;
(2)将条形统计图补充完整
(3)求该校各班在这一活动中植树的平均棵数
解:(1)3÷25%=12.
答:该校的班级总数是12.
(2)植树11棵的班级数是12-1-2-3-4=2.
补充条形图如图所示.
(3)(8×1+9×2+11×2+12×3+15×4)÷12=12(棵).
答:该校各班在这一活动中植树的平均棵数是12棵.
变式1、一组数据4,10,12,14,则这组数据的平均数是( )
A.9 B.10 C.11 D.12
B
例2、学校准备从甲、乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面进行了测试,他们各自的成绩(百分制)如下表:
{5940675A-B579-460E-94D1-54222C63F5DA}选手
表达能力
阅读理解
综合素质
汉字听写
甲
85
78
85
73
乙
73
80
82
83
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的
平均成绩,从他们的这一成绩看,应选派谁?
(2)如果表达能力、阅读理解、综合素质和汉字听写分别
赋予它们2,1,3和4的权,请分别计算两位选手的平均
成绩,从他们的这一成绩看,应选派谁?
变式2、某中学规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%,小桐的三项成绩(百分制)依次为95,90,85,则小桐这学期的体育成绩是( )
A.88.5 B.86.5 C.90 D.90.5
A
例3、一次数学测试,某小组5名同学的成绩统计如下(有两个数据被遮盖):
则被遮盖的两个数据依次是( )
A.80,80 B.81,80
C.80,82 D.81,82
{5940675A-B579-460E-94D1-54222C63F5DA}组员
甲
乙
丙
丁
戊
平均成绩
众数
得分
81
77
■
80
82
80
■
A
变式3、某中学开展“读书伴我成长”活动,为了解八年级学生四月份的读书册数,对从中随机抽取的20名学生的读书册数进行调查,结果如下表:
{5940675A-B579-460E-94D1-54222C63F5DA}册数/册
1
2
3
4
5
人数/人
2
5
7
4
2
根据统计表中的数据,这20名同学读书册数的众数、中位数分别是( )
A.3,3 B.3,7 C.2,7 D.7,3
D
例4、今年是我市全面推进中小学校“社会主义核心价值观”教育年,某校对全校学生进行了中期检测评价,检测结果分为A(优秀),B(良好),C(合格),D(不合格)四个等级,并随机抽取若干名学生的检测结果作为样本进行数据处理,制作了如下所示不完整的统计表和统计图.
{5940675A-B579-460E-94D1-54222C63F5DA}等级
频数
频率
A
a
0.3
B
35
0.35
C
31
b
D
4
0.04
请根据统计图和统计表提供的信息,解答下列问题:
(1)本次随机抽取了________名学生的检测结果;
(2)a=________,b=________;
100
30
0.31
解:补全的条形图如图所示.
(3)请补全条形图;
例5、为助力新冠肺炎疫情后经济的复苏,天天快餐公司积极投入到复工复产中.现有A,B两家农副产品加工厂到该公司推销鸡腿,两家鸡腿的价格相同,品质相近.该公司决定通过检查质量来确定选购哪家的鸡腿,检查人员从两家分别抽取100个鸡腿,然后再从中随机各抽取10个,记录它们的质量(单位:克)如下表:
{5940675A-B579-460E-94D1-54222C63F5DA}A加工厂
74
75
75
75
73
77
78
72
76
75
B加工厂
78
74
78
73
74
75
74
74
75
75
(1)根据表中数据,求A加工厂的10个鸡腿质量的中位数、众数、
平均数;
(2)估计B加工厂这100个鸡腿中,质量为75克的鸡腿有多少个.
(3)根据鸡腿质量的稳定性,该快餐公司应选购哪家加工厂的鸡腿?
(3)因为A,B加工厂的鸡腿质量的平均数一样,B加工厂的鸡腿质量的方差比A加工厂小,所以B加工厂的鸡腿质量更稳定,所以选购B加工厂的鸡腿.
变式4、甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字个数的统计结果如下表:
{5940675A-B579-460E-94D1-54222C63F5DA}班级
参赛人数
平均数(个)
中位数(个)
方差
甲班
55
135
149
191
乙班
55
135
151
110
某同学分析该表后得出如下结论:
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字的个数≥150为优秀);
③甲班成绩的波动比乙班大;
上述结论中,正确的是( )
A.①② B.②③ C.①③ D.①②③
D
变式5、小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,
所测成绩如图所示,请根据图
中信息解答以下问题:
(1)补全下面的表格.
次数
1
2
3
4
5
小明
13.3
13.3
13.2
13.3
小亮
13.2
13.4
13.1
13.3
13.4
13.5
(2) 分别计算成绩的平均数和方差,填入表格. 若你是老师,将小明与小亮的成绩比较析后, 将分别给予他们怎样的建议?
平均数
方差
小明
小亮
13.3
13.3
0.02
0.004
解:从平均数看,两人的平均水平相同;从方差看,小明的成绩较稳定,小亮的成绩波动较大.
给小明的建议是:加强锻炼,提高爆发力,提升短跑成绩;
给小亮的建议是:总结经验,找出成绩忽高忽低的原因,在稳定中提高.
例6、如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图,则下列判断错误的是( )
A.甲的数学成绩高于班级
平均分,且成绩比较稳定
B.乙的数学成绩在班级
平均分附近波动,且比丙好
C.丙的数学成绩低于班级平均分,但成绩逐次提高
D.就甲、乙、丙三个人而言,乙的数学成绩最不稳定
D
变式6、水稻种植是嘉兴的传统农业,为了比较甲、乙两种水稻的长势,农技人员从两块试验田中分别随机抽取5棵植株,将测得的苗高数据绘制成如图所示的统计图.请你根据统计图所提供的数据,计算甲、
乙两种水稻植株高度的平均数
和方差,并比较这两种水稻的
长势.
解:x甲=5.8 cm,x乙=5.8 cm,
甲种水稻植株高度的方差为2.16,乙种水稻植株高度的方差为0.56.
这两种水稻植株的平均高度相同,但乙种水稻比甲种水稻长得更整齐一些.
数据的整理与
初步处理
数据的一般水
平或集中趋势
数据的离散程
度或波动大小
平均数、
加权平均数
中位数
众数
方差
计
算
公
式
课堂小结
第20章 数据的整理与初步处理
要点梳理
一、数据的集中趋势
平均数
定义
一组数据的平均值称为这组数据的平均数
算术平
均数
一般地,如果有n个数x1,x2,…,xn,那么_____________________叫做这n个数的平均数.
加权平
均数
一般地,若n个数x1,x2,…,xn的权分别
是w1,w2,…,wn,则
___________________
叫做这n个数的加权平均数.
最多
中间位置的数
两个数据的平均数
中位数
定义
将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于________________就是这组数据的中位数,如果数据的个数是偶数,则中间_________________________就是这组数据的中位数
防错
提醒
确定中位数时,一定要注意先把整组数据按照大小顺序排列,再确定
众
数
定义
一组数据中出现次数________的数据叫做这组数据的众数
防错
提醒
(1)一组数据中众数不一定只有一个;(2)当一组数据中出现异常值时,其平均数往往不能正确反映这组数据的集中趋势,就应考虑用中位数或众数来分析
二、数据的波动程度
平均数
大
表示波
动的量
定义
意义
方差
设有n个数据x1,x2,x3,…,xn,各数据与它们的________的差的平方分别是(x1-x)2,(x2-x)2,…,(xn-x)2,我们用它们的平均数,即用________________________来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作s2
方差越大,数据的波动越___,反之也成立
例1、今年我市将创建全国森林城市,提出了“共建绿色城”的倡议.某校积极响应,在3月12日植树节这天组织全校学生开展了植树活动,校团委对全校各班的植树情况进行了统计,绘制了如图所示的两幅不完整的统计图.
(1)求该校的班级总数;
(2)将条形统计图补充完整
(3)求该校各班在这一活动中植树的平均棵数
解:(1)3÷25%=12.
答:该校的班级总数是12.
(2)植树11棵的班级数是12-1-2-3-4=2.
补充条形图如图所示.
(3)(8×1+9×2+11×2+12×3+15×4)÷12=12(棵).
答:该校各班在这一活动中植树的平均棵数是12棵.
变式1、一组数据4,10,12,14,则这组数据的平均数是( )
A.9 B.10 C.11 D.12
B
例2、学校准备从甲、乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面进行了测试,他们各自的成绩(百分制)如下表:
{5940675A-B579-460E-94D1-54222C63F5DA}选手
表达能力
阅读理解
综合素质
汉字听写
甲
85
78
85
73
乙
73
80
82
83
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的
平均成绩,从他们的这一成绩看,应选派谁?
(2)如果表达能力、阅读理解、综合素质和汉字听写分别
赋予它们2,1,3和4的权,请分别计算两位选手的平均
成绩,从他们的这一成绩看,应选派谁?
变式2、某中学规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%,小桐的三项成绩(百分制)依次为95,90,85,则小桐这学期的体育成绩是( )
A.88.5 B.86.5 C.90 D.90.5
A
例3、一次数学测试,某小组5名同学的成绩统计如下(有两个数据被遮盖):
则被遮盖的两个数据依次是( )
A.80,80 B.81,80
C.80,82 D.81,82
{5940675A-B579-460E-94D1-54222C63F5DA}组员
甲
乙
丙
丁
戊
平均成绩
众数
得分
81
77
■
80
82
80
■
A
变式3、某中学开展“读书伴我成长”活动,为了解八年级学生四月份的读书册数,对从中随机抽取的20名学生的读书册数进行调查,结果如下表:
{5940675A-B579-460E-94D1-54222C63F5DA}册数/册
1
2
3
4
5
人数/人
2
5
7
4
2
根据统计表中的数据,这20名同学读书册数的众数、中位数分别是( )
A.3,3 B.3,7 C.2,7 D.7,3
D
例4、今年是我市全面推进中小学校“社会主义核心价值观”教育年,某校对全校学生进行了中期检测评价,检测结果分为A(优秀),B(良好),C(合格),D(不合格)四个等级,并随机抽取若干名学生的检测结果作为样本进行数据处理,制作了如下所示不完整的统计表和统计图.
{5940675A-B579-460E-94D1-54222C63F5DA}等级
频数
频率
A
a
0.3
B
35
0.35
C
31
b
D
4
0.04
请根据统计图和统计表提供的信息,解答下列问题:
(1)本次随机抽取了________名学生的检测结果;
(2)a=________,b=________;
100
30
0.31
解:补全的条形图如图所示.
(3)请补全条形图;
例5、为助力新冠肺炎疫情后经济的复苏,天天快餐公司积极投入到复工复产中.现有A,B两家农副产品加工厂到该公司推销鸡腿,两家鸡腿的价格相同,品质相近.该公司决定通过检查质量来确定选购哪家的鸡腿,检查人员从两家分别抽取100个鸡腿,然后再从中随机各抽取10个,记录它们的质量(单位:克)如下表:
{5940675A-B579-460E-94D1-54222C63F5DA}A加工厂
74
75
75
75
73
77
78
72
76
75
B加工厂
78
74
78
73
74
75
74
74
75
75
(1)根据表中数据,求A加工厂的10个鸡腿质量的中位数、众数、
平均数;
(2)估计B加工厂这100个鸡腿中,质量为75克的鸡腿有多少个.
(3)根据鸡腿质量的稳定性,该快餐公司应选购哪家加工厂的鸡腿?
(3)因为A,B加工厂的鸡腿质量的平均数一样,B加工厂的鸡腿质量的方差比A加工厂小,所以B加工厂的鸡腿质量更稳定,所以选购B加工厂的鸡腿.
变式4、甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字个数的统计结果如下表:
{5940675A-B579-460E-94D1-54222C63F5DA}班级
参赛人数
平均数(个)
中位数(个)
方差
甲班
55
135
149
191
乙班
55
135
151
110
某同学分析该表后得出如下结论:
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字的个数≥150为优秀);
③甲班成绩的波动比乙班大;
上述结论中,正确的是( )
A.①② B.②③ C.①③ D.①②③
D
变式5、小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,
所测成绩如图所示,请根据图
中信息解答以下问题:
(1)补全下面的表格.
次数
1
2
3
4
5
小明
13.3
13.3
13.2
13.3
小亮
13.2
13.4
13.1
13.3
13.4
13.5
(2) 分别计算成绩的平均数和方差,填入表格. 若你是老师,将小明与小亮的成绩比较析后, 将分别给予他们怎样的建议?
平均数
方差
小明
小亮
13.3
13.3
0.02
0.004
解:从平均数看,两人的平均水平相同;从方差看,小明的成绩较稳定,小亮的成绩波动较大.
给小明的建议是:加强锻炼,提高爆发力,提升短跑成绩;
给小亮的建议是:总结经验,找出成绩忽高忽低的原因,在稳定中提高.
例6、如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图,则下列判断错误的是( )
A.甲的数学成绩高于班级
平均分,且成绩比较稳定
B.乙的数学成绩在班级
平均分附近波动,且比丙好
C.丙的数学成绩低于班级平均分,但成绩逐次提高
D.就甲、乙、丙三个人而言,乙的数学成绩最不稳定
D
变式6、水稻种植是嘉兴的传统农业,为了比较甲、乙两种水稻的长势,农技人员从两块试验田中分别随机抽取5棵植株,将测得的苗高数据绘制成如图所示的统计图.请你根据统计图所提供的数据,计算甲、
乙两种水稻植株高度的平均数
和方差,并比较这两种水稻的
长势.
解:x甲=5.8 cm,x乙=5.8 cm,
甲种水稻植株高度的方差为2.16,乙种水稻植株高度的方差为0.56.
这两种水稻植株的平均高度相同,但乙种水稻比甲种水稻长得更整齐一些.
数据的整理与
初步处理
数据的一般水
平或集中趋势
数据的离散程
度或波动大小
平均数、
加权平均数
中位数
众数
方差
计
算
公
式
课堂小结
