上海市长宁区2020-2021学年七年级上学期数学期末检测卷沪教版(word含答案)
文档属性
| 名称 | 上海市长宁区2020-2021学年七年级上学期数学期末检测卷沪教版(word含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 166.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-22 00:00:00 | ||
图片预览



文档简介
上海市长宁区2021年七年级上学期数学期末检测卷
考试时间:120分钟
总分:120分
学校:
班级:
姓名:
考号:
选择题(共10小题,每小题3分,共30分)
1.如果一个物体向右移动2米记作移动+2米,那么这个物体又移动了﹣2米的意思是( )
A.物体又向右移动了2米
B.物体又向右移动了4米
C.物体又向左移动了2米
D.物体又向左移动了4米
2.如图所示的几何体,从上面看得到的图形是( )
A.
B.
C.
D.
3.下列说法中,不正确的是( )
A.﹣ab2c的系数是﹣1,次数是4
B.﹣1是整式
C.6x2﹣3x+1的项是6x2、﹣3x,1
D.2πR+πR2是三次二项式
4.如图,直线AB、CD相交于点O,OE平分∠AOC,若∠BOD=70°,则∠COE的度数是( )
A.70°
B.50°
C.40°
D.35°
第4题图
第5题图
5.如图,下面哪个条件能判断DE∥BC的是( )
A.∠1=∠2
B.∠4=∠C
C.∠1+∠3=180°
D.∠3+∠C=180°
6.若x=0是方程的解,则k值为( )
A.0
B.2
C.3
D.4
7.某商品的进价是500元,标价是750元,商店要求以利润率为5%的售价打折出售,售货员可以打几折出售此商品( )
A.5
B.6
C.7
D.8
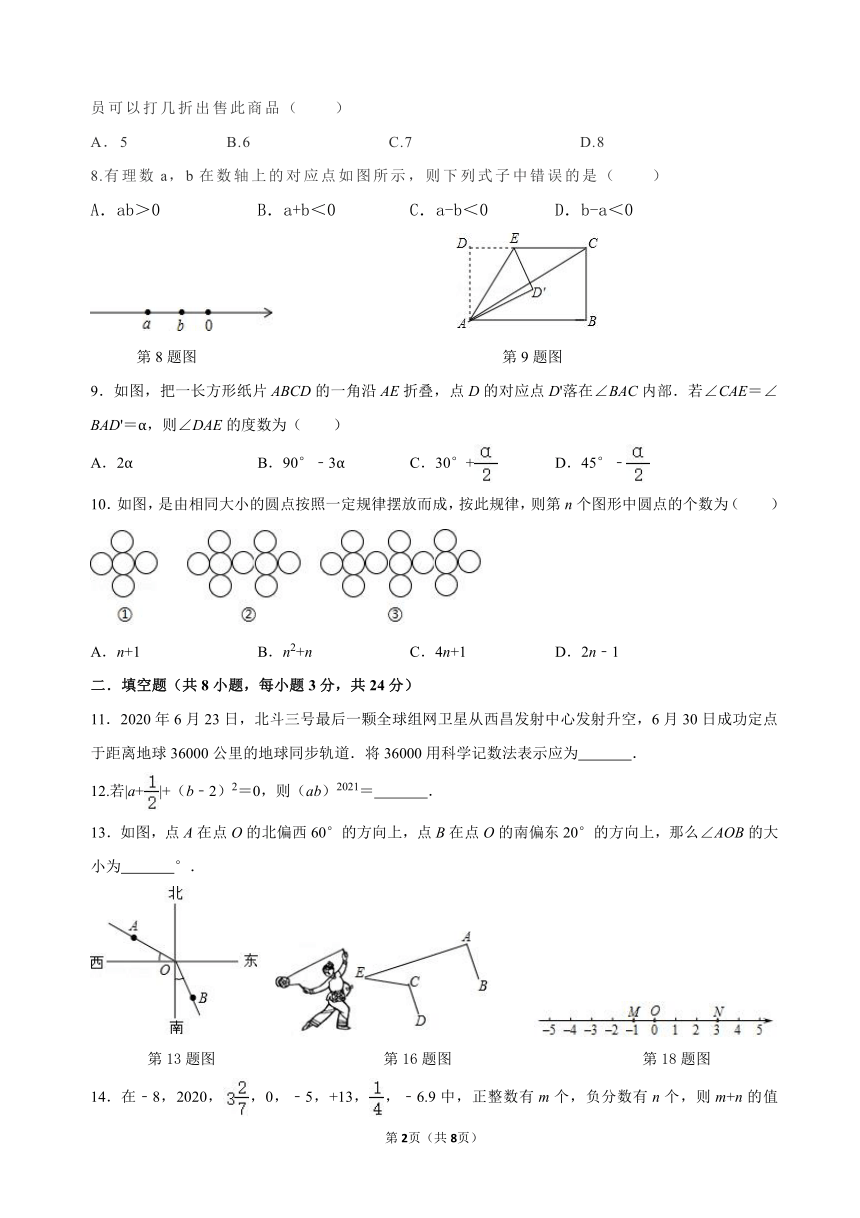
8.有理数a,b在数轴上的对应点如图所示,则下列式子中错误的是( )
ab>0
B.a+b<0
C.a-b<0
D.b-a<0
第8题图
第9题图
9.如图,把一长方形纸片ABCD的一角沿AE折叠,点D的对应点D'落在∠BAC内部.若∠CAE=∠BAD'=α,则∠DAE的度数为( )
A.2α
B.90°﹣3α
C.30°+
D.45°﹣
10.如图,是由相同大小的圆点按照一定规律摆放而成,按此规律,则第n个图形中圆点的个数为( )
n+1
B.n2+n
C.4n+1
D.2n﹣1
二.填空题(共8小题,每小题3分,共24分)
11.2020年6月23日,北斗三号最后一颗全球组网卫星从西昌发射中心发射升空,6月30日成功定点于距离地球36000公里的地球同步轨道.将36000用科学记数法表示应为
.
12.若|a+|+(b﹣2)2=0,则(ab)2021=
.
13.如图,点A在点O的北偏西60°的方向上,点B在点O的南偏东20°的方向上,那么∠AOB的大小为
°.
第13题图
第16题图
第18题图
在﹣8,2020,,0,﹣5,+13,,﹣6.9中,正整数有m个,负分数有n个,则m+n的值为
.
已知A、B、C是同一直线上的三个点,且AB=9,BC=4,D是BC的中点,则AD的长是
.
欢欢观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=115°,则∠E的度数是
.
5点40分时,钟表上时针和分针所成的角度是
.
如图,已知数轴上三点M,O,N对应的数分别为-1,0,3,点P为数轴上任意一点,其对应的数为x.如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动,设t分钟时点P到点M、点N的距离相等,则t的值为
.
三.解答题(共8小题,共66分)
19.(6分)计算:
(1)()×(﹣24)
(2)(﹣10)3+[(﹣4)2﹣(1﹣32)×2]
20.(6分)解方程:
(1)﹣3(x+1)=9
(2)﹣2=
21.(8分)如图,△ABC中,A(-2,1)、B(-4,-2)、C(-1,-3),△A'B'C'是△ABC平移之后得到的图象,并且C的对应点C'的坐标为(4,1).
A'、B'两点的坐标分别为A'
,B'
;
作出△ABC平移之后的图形△A'B'C';
(3)求△A'B'C'的面积.
22.(10分)一个正方体的六个面分别标有字母A,B,C,D,E,F,从三个不同方向看到的情形如图.
(1)A对面的字母是
,B对面的字母是
;(请直接填写答案)
(2)已知A=x,B=﹣x2+3x,C=﹣3,D=1,E=x2021,F=6.
①若字母A表示的数与它对面的字母表示的数互为相反数,求E的值;
②若2A﹣3B+M=0,求出M的表达式.
23.(8分)如图,DE平分∠ADF,DF∥BC,点E,F在线段AC上,点A,D,B在一直线上,连接BF.
(1)若∠ADF=70°,∠ABF=25°,求∠CBF的度数;
(2)若BF平分∠ABC时,求证:BF∥DE.
(8分)某车间为提高生产总量,在原有16名工人的基础上,新调入若干名工人,使得调整后车间的总人数是调入工人人数的3倍多4人.
(1)调入多少名工人;
(2)在(1)的条件下,每名工人每天可以生产1200个螺柱或2000个螺母,1个螺柱需要2个螺母,为使每天生产的螺柱和螺母刚好配套,应该安排生产螺柱和螺母的工人各多少名?
25.(8分)如图,C为线段AB上一点,D在线段AC上,且AD=AC,E为BC的中点.
(1)若AC=6,BE=1,求线段AB、DE的长;
(2)试说明:AB+BD=4DE.
26.(12分)如图,点O是直线AB上的一点,将一直角三角板如图摆放,过点O作射线OE平分∠BOC.
(1)如图1,如果∠AOC=40°,依题意补全图形,求∠DOE的度数;
(2)当直角三角板绕点O顺时针旋转一定的角度得到图2,使得直角边OC在直线AB的上方,若∠AOC=α,其他条件不变,请你用含α的代数式表示∠DOE的度数;
(3)当直角三角板绕点O继续顺时针旋转一周,回到图1的位置,在旋转过程中你发现∠AOC与∠DOE(0°≤∠AOC≤180°,0°≤∠DOE≤180°)之间有怎样的数量关系?请直接写出你的发现.
第1页(共8页)
答案解析:
1.C
2.D
3.D
4.D
5.C
6.C
7.C
8.D
9.D
10.C
解析:观察图形的变化可知:第1个图形中圆点的个数为4+1=5;第2个图形中圆点的个数为4×2+1=9;第3个图形中圆点的个数为4×3+1=13;
…发现规律,则第n个图形中圆点的个数为(4n+1).
故选:C.
11.3.6×104
12.-1
13.140
14.
3
15.
11或7
16.
23°
17.
70°
18.或4
解析:设运动t分钟时,点P到点M,点N的距离相等,即PM=PN.
点P对应的数是-t,点M对应的数是-1-2t,点N对应的数是3-3t.
①当点M和点N在点P同侧时,点M和点N重合,所以-1-2t=3-3t,解得t=4,符合题意.
②当点M和点N在点P异侧时,点M位于点P的左侧,点N位于点P的右侧(因为三个点都向左运动,出发时点M在点P左侧,且点M运动的速度大于点P的速度,所以点M永远位于点P的左侧),
故PM=-t-(-1-2t)=t+1.PN=(3-3t)-(-t)=3-2t.所以t+1=3-2t,解得t=,符合题意.
综上所述,t的值为或4.
19.(6分)解:(1)原式=×(﹣24)﹣×(﹣24)+×(﹣24)=﹣20+8﹣9=﹣21
(2)原式=(﹣1000)+[16﹣(1﹣9)×2]=(﹣1000)+[16﹣(﹣8)×2]
=(﹣1000)+(16+16)=(﹣1000)+32=﹣968.
20.(6分)解:(1)去括号,可得:﹣3x﹣3=9,
移项,合并同类项,可得:﹣3x=12,
系数化为1,可得:x=﹣4.
(2)去分母,可得:3(3x﹣1)﹣12=2(x﹣5),
去括号,可得:9x﹣3﹣12=2x﹣10,
移项,合并同类项,可得:7x=5,
系数化为1,可得:x=.
21.(8分)解:(1)(3,5)
(1,2)
(2)如图,△A'B'C'为所作;
(3)△A'B'C'的面积=3×4-×3×1-×4×1-×2×3=5.5.
22.(10分)解:(1)D
E
(2)①∵字母A表示的数与它对面的字母D表示的数互为相反数,
∴x=﹣1,∴E=(﹣1)2021=﹣1;
②∵2A﹣3B+M=0,∴2x﹣3(﹣x2+3x)+M=0,∴M=﹣2x+3(﹣x2+3x)=﹣3x2+7x.
23.(8分)解:(1)∵DF∥BC,∴∠ABC=∠ADF=70°,∵∠ABF=25°,∴∠CBF=70°-25°=45°;
(2)证明:∵DF∥BC,∴∠ABC=∠ADF,
∵BF平分∠ABC,DE平分∠ADF,∴∠ADE=∠ADF,∠ABF=∠ABC,
∴∠ADE=∠ABF,∴BF∥DE.
24.(8分)解:(1)设调入x名工人,根据题意得:16+x=3x+4,解得:x=6,则调入6名工人;
(2)16+6=22(人),设y名工人生产螺柱,
根据题意得:2×1200y=2000(22-y),解得:y=10,22-y=22-10=12(人),
则10名工人生产螺柱,12名工人生产螺母.
25.(8分)解:(1)∵E为BC的中点,BE=1,∴BC=2BE=2,CE=BE=1,
∵AC=6,∴AB=AC+BC=6+2=8,∵AD=AC,AC=6,∴AD=4,
∴DC=6﹣4=2,∴DE=DC+CE=2+1=3;
(2)∵AB=AC+BC,BD=BC+CD,∴AB+BD=AC+BC+BC+CD,
∵AD=AC,E为BC的中点,∴AC=3CD,BC=2CE,
∴AB+BD=3CD+2CE+2CE+CD=4CD+4CE=4(CD+CE)=4DE.
26.(12分)解:(1)如图1,补全图形;
∵∠AOC+∠BOC=180°,∠AOC=40°,∴∠BOC=140°;
又∵OE平分∠BOC,∴∠COE=70°;
∵∠COD=90°,∠COE=70°,∴∠DOE=20°.
(2)∵∠AOC+∠BOC=180°,∠AOC=α,∴∠BOC=180°﹣α;
∵OE平分∠BOC,∴∠COE=90°﹣α;
∵∠COD=90°,∠COE=90°﹣α,∴∠DOE=.
(3)∠DOE=∠AOC(0°≤∠AOC≤180°),∠DOE=180°∠AOC(0°≤∠DOE≤180°).
第8页(共8页)
考试时间:120分钟
总分:120分
学校:
班级:
姓名:
考号:
选择题(共10小题,每小题3分,共30分)
1.如果一个物体向右移动2米记作移动+2米,那么这个物体又移动了﹣2米的意思是( )
A.物体又向右移动了2米
B.物体又向右移动了4米
C.物体又向左移动了2米
D.物体又向左移动了4米
2.如图所示的几何体,从上面看得到的图形是( )
A.
B.
C.
D.
3.下列说法中,不正确的是( )
A.﹣ab2c的系数是﹣1,次数是4
B.﹣1是整式
C.6x2﹣3x+1的项是6x2、﹣3x,1
D.2πR+πR2是三次二项式
4.如图,直线AB、CD相交于点O,OE平分∠AOC,若∠BOD=70°,则∠COE的度数是( )
A.70°
B.50°
C.40°
D.35°
第4题图
第5题图
5.如图,下面哪个条件能判断DE∥BC的是( )
A.∠1=∠2
B.∠4=∠C
C.∠1+∠3=180°
D.∠3+∠C=180°
6.若x=0是方程的解,则k值为( )
A.0
B.2
C.3
D.4
7.某商品的进价是500元,标价是750元,商店要求以利润率为5%的售价打折出售,售货员可以打几折出售此商品( )
A.5
B.6
C.7
D.8
8.有理数a,b在数轴上的对应点如图所示,则下列式子中错误的是( )
ab>0
B.a+b<0
C.a-b<0
D.b-a<0
第8题图
第9题图
9.如图,把一长方形纸片ABCD的一角沿AE折叠,点D的对应点D'落在∠BAC内部.若∠CAE=∠BAD'=α,则∠DAE的度数为( )
A.2α
B.90°﹣3α
C.30°+
D.45°﹣
10.如图,是由相同大小的圆点按照一定规律摆放而成,按此规律,则第n个图形中圆点的个数为( )
n+1
B.n2+n
C.4n+1
D.2n﹣1
二.填空题(共8小题,每小题3分,共24分)
11.2020年6月23日,北斗三号最后一颗全球组网卫星从西昌发射中心发射升空,6月30日成功定点于距离地球36000公里的地球同步轨道.将36000用科学记数法表示应为
.
12.若|a+|+(b﹣2)2=0,则(ab)2021=
.
13.如图,点A在点O的北偏西60°的方向上,点B在点O的南偏东20°的方向上,那么∠AOB的大小为
°.
第13题图
第16题图
第18题图
在﹣8,2020,,0,﹣5,+13,,﹣6.9中,正整数有m个,负分数有n个,则m+n的值为
.
已知A、B、C是同一直线上的三个点,且AB=9,BC=4,D是BC的中点,则AD的长是
.
欢欢观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=115°,则∠E的度数是
.
5点40分时,钟表上时针和分针所成的角度是
.
如图,已知数轴上三点M,O,N对应的数分别为-1,0,3,点P为数轴上任意一点,其对应的数为x.如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动,设t分钟时点P到点M、点N的距离相等,则t的值为
.
三.解答题(共8小题,共66分)
19.(6分)计算:
(1)()×(﹣24)
(2)(﹣10)3+[(﹣4)2﹣(1﹣32)×2]
20.(6分)解方程:
(1)﹣3(x+1)=9
(2)﹣2=
21.(8分)如图,△ABC中,A(-2,1)、B(-4,-2)、C(-1,-3),△A'B'C'是△ABC平移之后得到的图象,并且C的对应点C'的坐标为(4,1).
A'、B'两点的坐标分别为A'
,B'
;
作出△ABC平移之后的图形△A'B'C';
(3)求△A'B'C'的面积.
22.(10分)一个正方体的六个面分别标有字母A,B,C,D,E,F,从三个不同方向看到的情形如图.
(1)A对面的字母是
,B对面的字母是
;(请直接填写答案)
(2)已知A=x,B=﹣x2+3x,C=﹣3,D=1,E=x2021,F=6.
①若字母A表示的数与它对面的字母表示的数互为相反数,求E的值;
②若2A﹣3B+M=0,求出M的表达式.
23.(8分)如图,DE平分∠ADF,DF∥BC,点E,F在线段AC上,点A,D,B在一直线上,连接BF.
(1)若∠ADF=70°,∠ABF=25°,求∠CBF的度数;
(2)若BF平分∠ABC时,求证:BF∥DE.
(8分)某车间为提高生产总量,在原有16名工人的基础上,新调入若干名工人,使得调整后车间的总人数是调入工人人数的3倍多4人.
(1)调入多少名工人;
(2)在(1)的条件下,每名工人每天可以生产1200个螺柱或2000个螺母,1个螺柱需要2个螺母,为使每天生产的螺柱和螺母刚好配套,应该安排生产螺柱和螺母的工人各多少名?
25.(8分)如图,C为线段AB上一点,D在线段AC上,且AD=AC,E为BC的中点.
(1)若AC=6,BE=1,求线段AB、DE的长;
(2)试说明:AB+BD=4DE.
26.(12分)如图,点O是直线AB上的一点,将一直角三角板如图摆放,过点O作射线OE平分∠BOC.
(1)如图1,如果∠AOC=40°,依题意补全图形,求∠DOE的度数;
(2)当直角三角板绕点O顺时针旋转一定的角度得到图2,使得直角边OC在直线AB的上方,若∠AOC=α,其他条件不变,请你用含α的代数式表示∠DOE的度数;
(3)当直角三角板绕点O继续顺时针旋转一周,回到图1的位置,在旋转过程中你发现∠AOC与∠DOE(0°≤∠AOC≤180°,0°≤∠DOE≤180°)之间有怎样的数量关系?请直接写出你的发现.
第1页(共8页)
答案解析:
1.C
2.D
3.D
4.D
5.C
6.C
7.C
8.D
9.D
10.C
解析:观察图形的变化可知:第1个图形中圆点的个数为4+1=5;第2个图形中圆点的个数为4×2+1=9;第3个图形中圆点的个数为4×3+1=13;
…发现规律,则第n个图形中圆点的个数为(4n+1).
故选:C.
11.3.6×104
12.-1
13.140
14.
3
15.
11或7
16.
23°
17.
70°
18.或4
解析:设运动t分钟时,点P到点M,点N的距离相等,即PM=PN.
点P对应的数是-t,点M对应的数是-1-2t,点N对应的数是3-3t.
①当点M和点N在点P同侧时,点M和点N重合,所以-1-2t=3-3t,解得t=4,符合题意.
②当点M和点N在点P异侧时,点M位于点P的左侧,点N位于点P的右侧(因为三个点都向左运动,出发时点M在点P左侧,且点M运动的速度大于点P的速度,所以点M永远位于点P的左侧),
故PM=-t-(-1-2t)=t+1.PN=(3-3t)-(-t)=3-2t.所以t+1=3-2t,解得t=,符合题意.
综上所述,t的值为或4.
19.(6分)解:(1)原式=×(﹣24)﹣×(﹣24)+×(﹣24)=﹣20+8﹣9=﹣21
(2)原式=(﹣1000)+[16﹣(1﹣9)×2]=(﹣1000)+[16﹣(﹣8)×2]
=(﹣1000)+(16+16)=(﹣1000)+32=﹣968.
20.(6分)解:(1)去括号,可得:﹣3x﹣3=9,
移项,合并同类项,可得:﹣3x=12,
系数化为1,可得:x=﹣4.
(2)去分母,可得:3(3x﹣1)﹣12=2(x﹣5),
去括号,可得:9x﹣3﹣12=2x﹣10,
移项,合并同类项,可得:7x=5,
系数化为1,可得:x=.
21.(8分)解:(1)(3,5)
(1,2)
(2)如图,△A'B'C'为所作;
(3)△A'B'C'的面积=3×4-×3×1-×4×1-×2×3=5.5.
22.(10分)解:(1)D
E
(2)①∵字母A表示的数与它对面的字母D表示的数互为相反数,
∴x=﹣1,∴E=(﹣1)2021=﹣1;
②∵2A﹣3B+M=0,∴2x﹣3(﹣x2+3x)+M=0,∴M=﹣2x+3(﹣x2+3x)=﹣3x2+7x.
23.(8分)解:(1)∵DF∥BC,∴∠ABC=∠ADF=70°,∵∠ABF=25°,∴∠CBF=70°-25°=45°;
(2)证明:∵DF∥BC,∴∠ABC=∠ADF,
∵BF平分∠ABC,DE平分∠ADF,∴∠ADE=∠ADF,∠ABF=∠ABC,
∴∠ADE=∠ABF,∴BF∥DE.
24.(8分)解:(1)设调入x名工人,根据题意得:16+x=3x+4,解得:x=6,则调入6名工人;
(2)16+6=22(人),设y名工人生产螺柱,
根据题意得:2×1200y=2000(22-y),解得:y=10,22-y=22-10=12(人),
则10名工人生产螺柱,12名工人生产螺母.
25.(8分)解:(1)∵E为BC的中点,BE=1,∴BC=2BE=2,CE=BE=1,
∵AC=6,∴AB=AC+BC=6+2=8,∵AD=AC,AC=6,∴AD=4,
∴DC=6﹣4=2,∴DE=DC+CE=2+1=3;
(2)∵AB=AC+BC,BD=BC+CD,∴AB+BD=AC+BC+BC+CD,
∵AD=AC,E为BC的中点,∴AC=3CD,BC=2CE,
∴AB+BD=3CD+2CE+2CE+CD=4CD+4CE=4(CD+CE)=4DE.
26.(12分)解:(1)如图1,补全图形;
∵∠AOC+∠BOC=180°,∠AOC=40°,∴∠BOC=140°;
又∵OE平分∠BOC,∴∠COE=70°;
∵∠COD=90°,∠COE=70°,∴∠DOE=20°.
(2)∵∠AOC+∠BOC=180°,∠AOC=α,∴∠BOC=180°﹣α;
∵OE平分∠BOC,∴∠COE=90°﹣α;
∵∠COD=90°,∠COE=90°﹣α,∴∠DOE=.
(3)∠DOE=∠AOC(0°≤∠AOC≤180°),∠DOE=180°∠AOC(0°≤∠DOE≤180°).
第8页(共8页)
同课章节目录
