2020-2021学年冀教版数学八年级下册21.2.1一次函数的图象课件(共22张)
文档属性
| 名称 | 2020-2021学年冀教版数学八年级下册21.2.1一次函数的图象课件(共22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 17:54:44 | ||
图片预览






文档简介
(共22张PPT)
21.2.1
一次函数的图象
八年级下册
理解一次函数的表达式与图象之间的对应关系
能较熟练作出一次函数的图象
通过实际操作与合作探究,掌握一次函数图象的画法,并初步感受其形象.
学习目标
1
2
3
能较熟练作出一次函数的图象
经历作图过程,理解一次函数的表达式与图象之间的对应关系
学习重难点
重点:
难点:
情景导入
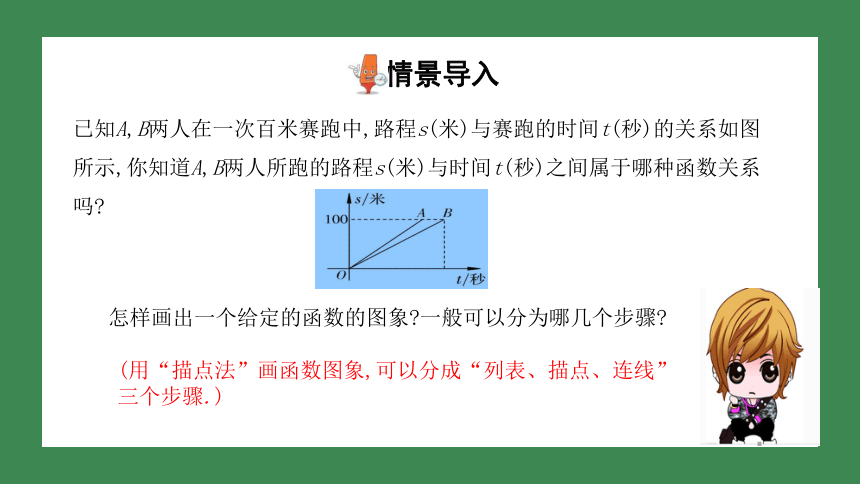
已知A,B两人在一次百米赛跑中,路程s(米)与赛跑的时间t(秒)的关系如图所示,你知道A,B两人所跑的路程s(米)与时间t(秒)之间属于哪种函数关系吗?
怎样画出一个给定的函数的图象?一般可以分为哪几个步骤?
(用“描点法”画函数图象,可以分成“列表、描点、连线”三个步骤.)
想一想
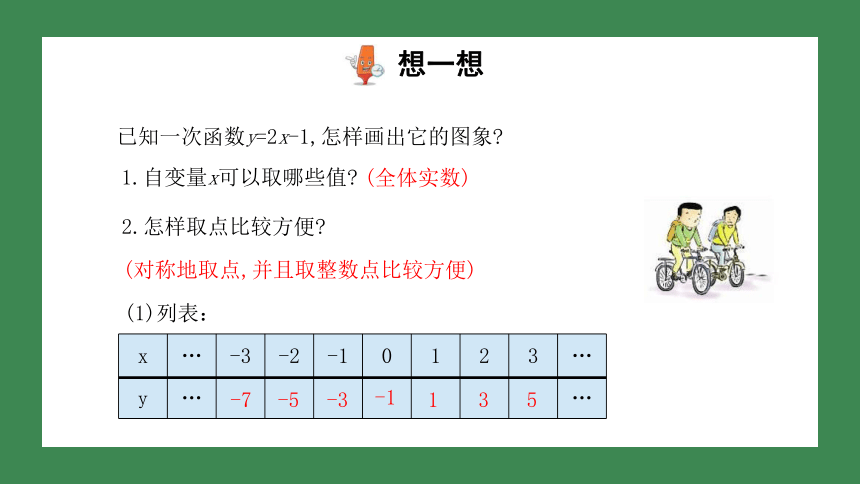
已知一次函数y=2x-1,怎样画出它的图象?
1.自变量x可以取哪些值?
(全体实数)
2.怎样取点比较方便?
(对称地取点,并且取整数点比较方便)
x
…
-3
-2
-1
0
1
2
3
…
y
…
…
-7
-5
-3
-1
1
3
5
(1)列表:
探究新知
以(1)中得到的每对对应值分别为横坐标和纵坐标,在图中所示的直角坐标系中,描出相应的点.
把(2)描出的点依次用平滑曲线连接起来,就得到y=2x-1的图象.
y
x
O
-1
-2
-3
-4
-5
-6
-7
5
4
3
2
1
-1
-2
-3
-4
4
3
2
1
(-2,-5)
(-3,-7)
(-1,-3)
(0,-1)
(1,1)
(2,3)
(3,5)
(2)描点:
(3)连线:
做一做
(1)一次函数y=2x-1的图象的形状是怎样的?
(3)一次函数的表达式与图象有何关系?
(2)凡是满足关系式y=2x-1的x,y的值所对应的点,
如
等,都在一次函数y=2x-1的图象上吗?
归纳总结
一次函数y=kx+b的图象也称为直线y=kx+b.
一次函数y=kx+b的图象是一条直线,因此画一次函数图象时,只要确定两个点,再过这两点画直线就可以了.一般过(0,b)和(1,k+b)或(,0)
(0,
b)
(,
0)
填一填
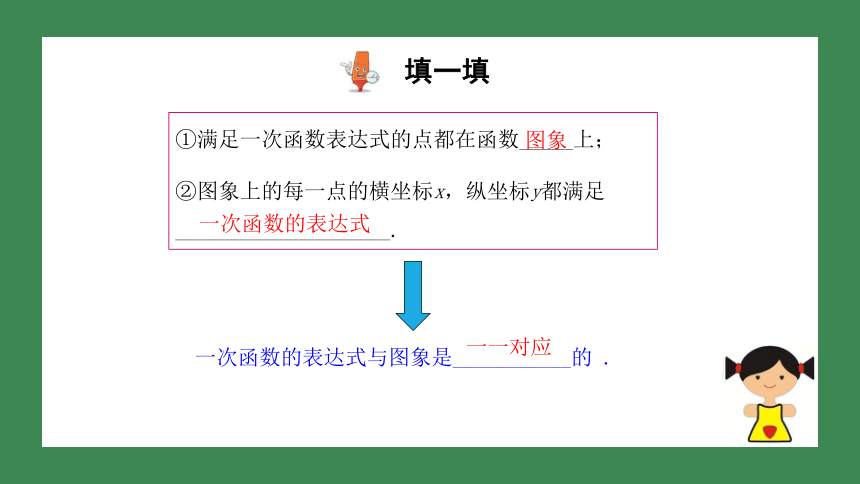
①满足一次函数表达式的点都在函数_____上;
②图象上的每一点的横坐标x,纵坐标y都满足____________________.
一次函数的表达式与图象是___________的
.
图象
一次函数的表达式
一一对应
画一画
列表
x
–2
–1
0
1
2
y=-2x+1
5
3
1
–1
–3
画出一次函数y=-2x+1的图象
描点
连线
典例精析
例1.画一次函数y=的图象.
一次函数
的图象.
O
y
x
2
1
(0,1)
(2,0)
解:当x=0时,y=1.
当y=0时,
,解得x=2.
在直角坐标系中,过点(0,1),(2,0)画直线,即得
做一做
O
用你认为最简单的方法画出下列函数的图象:
(1)y=-2x-1;(2)y=0.5x+1
x
0
1
y=-2x-1
y=0.5x+1
-1
-3
1
y=-2x-1
1.5
y=0.5x+1
也可以先画直线y=-2x与y=0.5x,再分别平移它们,也能得到直线y=-2x-1与y=0.5x+1
拓展延伸
在同一个平面直角坐标系中画出下列函数的图象.
(3)y=3x;
(4)y=3x+2.
认真观察上题画出的四个函数图象的特点,比较下列各对函数图象的相同点和不同点.
(1)y=3x与y=3x+2;
(3)y=3x+2与y=x+2.
由此你能发现什么规律?
归纳总结
对于一次函数
y=kx+b
和
y=k1x+b1:
(1)当k=k1,b≠b1时,两条直线平行,可以通过平移其中一条直线得到另一条直线;
(2)当k≠k1,b=b1时,两条直线相交,且交点在y轴上,是点(0,b).
课堂练习
1.
一次函数y=x-2的大致图象为(
)
C
课堂练习
2.当m=
时,函数y=(1-2m)x+m-1的图象过原点;
3.函数y=kx-1的图象过定点
;
4.若函数y=kx+b的图象过点(1
,2),则k+b=
.
1
(0,-1)
2
课堂练习
5.在同一直角坐标系中,画出y=x和y=1-x的图象.
(1,1)
O
y
x
2
1
2
1
y=x
y=1-x
解:如图所示.
思考:点(-4,5)在直线y=1-x上吗?
课堂练习
6.已知一次函数y=-2x-2.
(1)画出函数的图象;
(2)求图象与x轴,y轴的交点A,B的坐标;
(3)求A,B两点间的距离;
(4)求△AOB的面积;
(5)利用图象求当x为何值时,y≥0.
课堂练习
解:(1)如图所示的是一次函数y=-2x-2的图象.
(2)当y=0时,x=-1,所以一次函数图象与x轴的交点坐标是A(-1,0);
当x=0时,y=-2,所以一次函数图象与y轴的交点坐标是B(0,-2).
(3)用勾股定理可求AB的长,即AB=.
(4)
(5)由图象可知当x≤-1时,y≥0.
总结
一次函数的图象
画一次函数的图象
一次函数的表达式与图象的关系
列表、描点、连线
两点确定一条直线
图象上所有点的坐标满足函数表达式
坐标满足表达式的所有点都在函数图象上
课后作业
分别在同一坐标系内作出下列各组一次函数的图象:
(1)
(2)
(3)
谢谢听讲!
21.2.1
一次函数的图象
八年级下册
理解一次函数的表达式与图象之间的对应关系
能较熟练作出一次函数的图象
通过实际操作与合作探究,掌握一次函数图象的画法,并初步感受其形象.
学习目标
1
2
3
能较熟练作出一次函数的图象
经历作图过程,理解一次函数的表达式与图象之间的对应关系
学习重难点
重点:
难点:
情景导入
已知A,B两人在一次百米赛跑中,路程s(米)与赛跑的时间t(秒)的关系如图所示,你知道A,B两人所跑的路程s(米)与时间t(秒)之间属于哪种函数关系吗?
怎样画出一个给定的函数的图象?一般可以分为哪几个步骤?
(用“描点法”画函数图象,可以分成“列表、描点、连线”三个步骤.)
想一想
已知一次函数y=2x-1,怎样画出它的图象?
1.自变量x可以取哪些值?
(全体实数)
2.怎样取点比较方便?
(对称地取点,并且取整数点比较方便)
x
…
-3
-2
-1
0
1
2
3
…
y
…
…
-7
-5
-3
-1
1
3
5
(1)列表:
探究新知
以(1)中得到的每对对应值分别为横坐标和纵坐标,在图中所示的直角坐标系中,描出相应的点.
把(2)描出的点依次用平滑曲线连接起来,就得到y=2x-1的图象.
y
x
O
-1
-2
-3
-4
-5
-6
-7
5
4
3
2
1
-1
-2
-3
-4
4
3
2
1
(-2,-5)
(-3,-7)
(-1,-3)
(0,-1)
(1,1)
(2,3)
(3,5)
(2)描点:
(3)连线:
做一做
(1)一次函数y=2x-1的图象的形状是怎样的?
(3)一次函数的表达式与图象有何关系?
(2)凡是满足关系式y=2x-1的x,y的值所对应的点,
如
等,都在一次函数y=2x-1的图象上吗?
归纳总结
一次函数y=kx+b的图象也称为直线y=kx+b.
一次函数y=kx+b的图象是一条直线,因此画一次函数图象时,只要确定两个点,再过这两点画直线就可以了.一般过(0,b)和(1,k+b)或(,0)
(0,
b)
(,
0)
填一填
①满足一次函数表达式的点都在函数_____上;
②图象上的每一点的横坐标x,纵坐标y都满足____________________.
一次函数的表达式与图象是___________的
.
图象
一次函数的表达式
一一对应
画一画
列表
x
–2
–1
0
1
2
y=-2x+1
5
3
1
–1
–3
画出一次函数y=-2x+1的图象
描点
连线
典例精析
例1.画一次函数y=的图象.
一次函数
的图象.
O
y
x
2
1
(0,1)
(2,0)
解:当x=0时,y=1.
当y=0时,
,解得x=2.
在直角坐标系中,过点(0,1),(2,0)画直线,即得
做一做
O
用你认为最简单的方法画出下列函数的图象:
(1)y=-2x-1;(2)y=0.5x+1
x
0
1
y=-2x-1
y=0.5x+1
-1
-3
1
y=-2x-1
1.5
y=0.5x+1
也可以先画直线y=-2x与y=0.5x,再分别平移它们,也能得到直线y=-2x-1与y=0.5x+1
拓展延伸
在同一个平面直角坐标系中画出下列函数的图象.
(3)y=3x;
(4)y=3x+2.
认真观察上题画出的四个函数图象的特点,比较下列各对函数图象的相同点和不同点.
(1)y=3x与y=3x+2;
(3)y=3x+2与y=x+2.
由此你能发现什么规律?
归纳总结
对于一次函数
y=kx+b
和
y=k1x+b1:
(1)当k=k1,b≠b1时,两条直线平行,可以通过平移其中一条直线得到另一条直线;
(2)当k≠k1,b=b1时,两条直线相交,且交点在y轴上,是点(0,b).
课堂练习
1.
一次函数y=x-2的大致图象为(
)
C
课堂练习
2.当m=
时,函数y=(1-2m)x+m-1的图象过原点;
3.函数y=kx-1的图象过定点
;
4.若函数y=kx+b的图象过点(1
,2),则k+b=
.
1
(0,-1)
2
课堂练习
5.在同一直角坐标系中,画出y=x和y=1-x的图象.
(1,1)
O
y
x
2
1
2
1
y=x
y=1-x
解:如图所示.
思考:点(-4,5)在直线y=1-x上吗?
课堂练习
6.已知一次函数y=-2x-2.
(1)画出函数的图象;
(2)求图象与x轴,y轴的交点A,B的坐标;
(3)求A,B两点间的距离;
(4)求△AOB的面积;
(5)利用图象求当x为何值时,y≥0.
课堂练习
解:(1)如图所示的是一次函数y=-2x-2的图象.
(2)当y=0时,x=-1,所以一次函数图象与x轴的交点坐标是A(-1,0);
当x=0时,y=-2,所以一次函数图象与y轴的交点坐标是B(0,-2).
(3)用勾股定理可求AB的长,即AB=.
(4)
(5)由图象可知当x≤-1时,y≥0.
总结
一次函数的图象
画一次函数的图象
一次函数的表达式与图象的关系
列表、描点、连线
两点确定一条直线
图象上所有点的坐标满足函数表达式
坐标满足表达式的所有点都在函数图象上
课后作业
分别在同一坐标系内作出下列各组一次函数的图象:
(1)
(2)
(3)
谢谢听讲!
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
