云南省昆明新世纪高级中学2012届高三第五次月考 理科数学试题
文档属性
| 名称 | 云南省昆明新世纪高级中学2012届高三第五次月考 理科数学试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 272.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-26 00:00:00 | ||
图片预览




文档简介
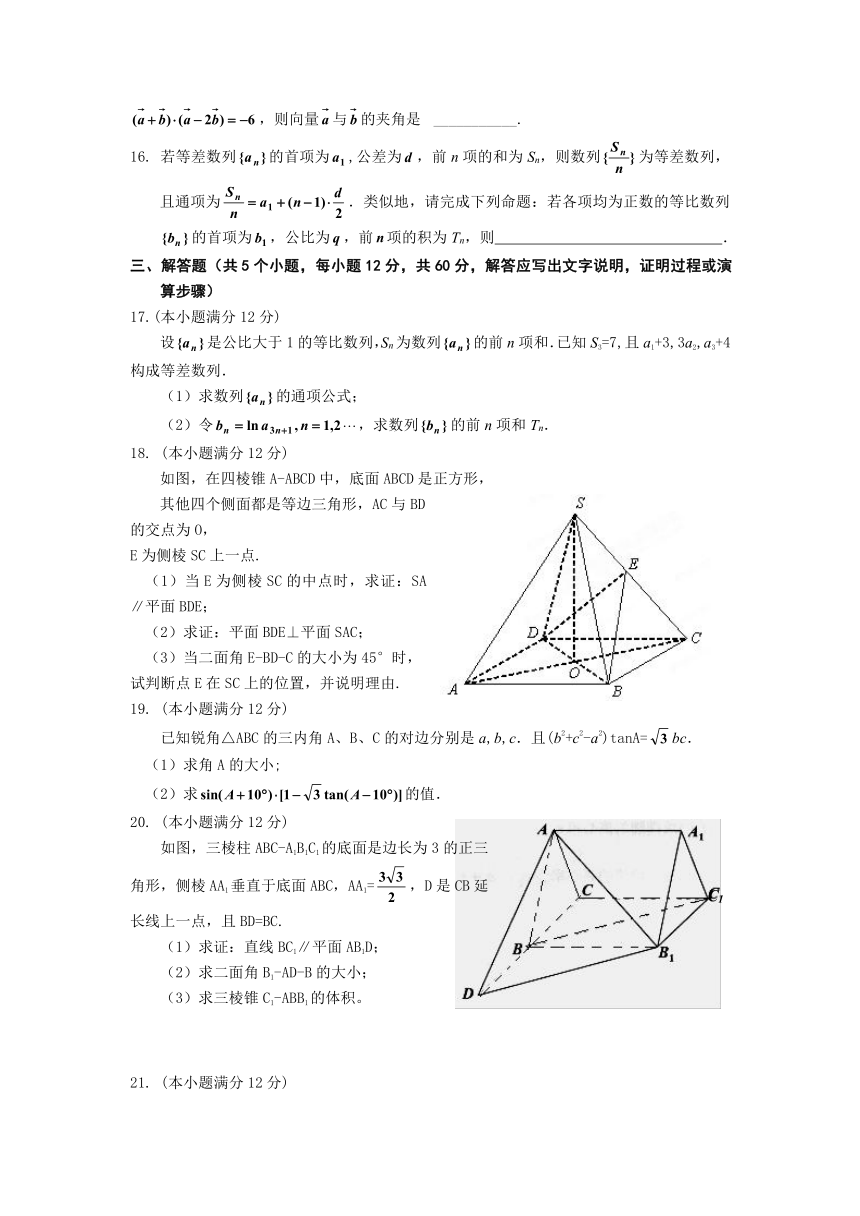
绝密★启用前
昆明市五华区新世纪高级中学2012届高三第五次模拟考试题
理科数学
考试时间:2011年12月31日上午8:00-10:00,共120分钟 命题人:杨先明
题号 一 二 三 总分
得分
注意事项:
1.答题前,考生务必用黑色碳素笔将自己的姓名、考号、考场号、座位号等在答题卡上填写清楚,并认真核准。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案的标号。在试题卷上作答无效。
参考公式:
如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么 其中R表示球的半径
P(A·B)=P(A)·P(B) 球的体积公式
如果事件A在一次试验中发生的概率是
P,那么n次独立重复试验中恰好发生k次的概率 其中R表示球的半径
一、选择题(本大题共12小题,每小题5分,满分60分)
1.i为虚数单位,复平面内表示复数的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知集合,则=( )
A. B. C. D.
4.已知等比数列的公比为正数,且,则=( )
A. B. C. D.2
5.已知变量x、y满足的约束条件,则的最大值为( )
A.-3 B. C.-5 D.4
6.过点(0,1)且与曲线在点(3,2)处的切线垂直的直线的方程为( )
A. B. C. D.
7.为了得到函数的图像,只需把函数的图像( )
A.向左平移个长度单位 B.向右平移个长度单位
C.向左平移个长度单位 D.向右平移个长度单位
8.关于直线与平面,有以下四个命题:
①若,则 ②若
③若 ④若
其中真命题有( )
A.1个 B.2个 C.3个 D.4个
9. 若函数的导函数,则使得函数单调递减的一个充分不必要条件是x∈( )
A.[0,1] B.[3,5] C.[2,3] D.[2,4]
10.设若,则的值是( )
A. -1 B. 2 C. 1 D.-2
11.△ABC中,∠A=60°,∠A的平分线AD交边BC于D,已知AB=3,且,则AD的长为( )
A.1 B. C. D.3
12.在三棱锥S—ABC中,AB⊥BC,AB=BC=,SA=SC=2,,二面角S—AC—B的余弦值是,若S、A、B、C都在同一球面上,则该球的表面积是( )
A. B. C.24 D.6
二、填空题(本大题共4小题,每小题5分,共20分)
13. 在△ABC中,B=中,且,则△ABC的面积是_____
14. 某几何体的三视图如图所示,则它的体积是________.
15. 已知向量满足:,且,则向量与的夹角是 ___________.
16. 若等差数列的首项为,公差为,前n项的和为Sn,则数列为等差数列,且通项为.类似地,请完成下列命题:若各项均为正数的等比数列的首项为,公比为,前项的积为Tn,则 .
三、解答题(共5个小题,每小题12分,共60分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分12分)
设是公比大于1的等比数列,Sn为数列的前n项和.已知S3=7,且a1+3,3a2,a3+4构成等差数列.
(1)求数列的通项公式;
(2)令,求数列的前n项和Tn.
18. (本小题满分12分)
如图,在四棱锥A-ABCD中,底面ABCD是正方形,
其他四个侧面都是等边三角形,AC与BD的交点为O,
E为侧棱SC上一点.
(1)当E为侧棱SC的中点时,求证:SA∥平面BDE;
(2)求证:平面BDE⊥平面SAC;
(3)当二面角E-BD-C的大小为45°时,
试判断点E在SC上的位置,并说明理由.
19. (本小题满分12分)
已知锐角△ABC的三内角A、B、C的对边分别是a,b,c.且(b2+c2-a2)tanA=bc.
(1)求角A的大小;
(2)求的值.
20. (本小题满分12分)
如图,三棱柱ABC-A1B1C1的底面是边长为3的正三
角形,侧棱AA1垂直于底面ABC,AA1=,D是CB延
长线上一点,且BD=BC.
(1)求证:直线BC1∥平面AB1D;
(2)求二面角B1-AD-B的大小;
(3)求三棱锥C1-ABB1的体积。
21. (本小题满分12分)
已知函数.
(1)当且,时,试用含的式子表示,并讨论的单调区间;
(2)若有零点,,且对函数定义域内一切满足|x|≥2的实数x有≥0.
①求的表达式;
②当时,求函数的图象与函数的图象的交点坐标.
四、选考题(本小题满分10分)(请考生在22,23,24三题中任选一题做答,如果多做,则按所做的第一题记分.做答时用2B铅笔在答题卡把所选题目的题号涂黑)
23.选修4—4:坐标系与参数方程
以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线经过点P(1,1),倾斜角.
(1)写出直线的参数方程;
(2)设与圆相交于两点A、B,求点P到A、B两点的距离之积.
24.选修4—5:不等式选讲
已知函数f(x)=|2x-a|+a.
(1)若不等式f(x)≤6的解集为{x|-2≤x≤3},求实数a的值;
(2)在(1)的条件下,若存在实数n使f(n)≤m-f(-n)成立,求实数m的取值范围.
昆明市五华区新世纪高级中学2012届高三第五次模拟考试题
理科数学评分标准
一、选择题(12*5分=60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C D B B D A A B C C C D
二、填空题(4*5分=20分)
13、6 14.、 15、 16、
三、解答题(5*12分=60分)
17.解:(Ⅰ)设数列的公比为,
由已知,得 , ……………………………………2分
即, 也即
解得 ………………………………………………………………………5分
故数列的通项为. ………………………………………………6分
(Ⅱ)由(Ⅰ)得, ∴ , …………8分
又,
∴ 是以为首项,以为公差的等差数列 ……………10分
∴
即. ……………………………………………………………12分
18.证明:(Ⅰ)连接,由条件可得∥.
因为平面,平面,
所以∥平面.
(Ⅱ)法一:证明:由已知可得,,是中点,
所以,
又因为四边形是正方形,所以.
因为,所以
又因为,所以平面平面. -
(Ⅱ)法二:证明:由(Ⅰ)知,.
建立如图所示的空间直角坐标系.
设四棱锥的底面边长为2,
则,,,
,,.
所以,.
设(),由已知可求得.
所以,.
设平面法向量为,
则 即
令,得.
易知是平面的法向量.
因为,
所以,所以平面平面. -------------------(8分)
19.解:(1)由已知:
∴ ∴锐角△ABC ∴
(2)原式=
=
=
(Ⅱ)过作于,连结
平面,,
是二面角的平面角。
,是的中点,。
在中,
,即二面角的大小为60°
(Ⅲ)过作于,
平面,平面平面,
平面且为点到平面的距离。
,
。
21.解:(1) ………………2分
由,故
时 由 得的单调增区间是,
由 得单调减区间是
同理时,的单调增区间,,单调减区间为 …5分
(2)①由(1)及 (i)
又由 有知的零点在内,设,
则,结合(i)解得, …8分
∴ ………………9分
②又设,先求与轴在的交点
∵, 由 得
故,在单调递增
又,故与轴有唯一交点
即与的图象在区间上的唯一交点坐标为为所求 …………12分
四、选考题(10分)
22.
解析:(I)连接DE,根据题意在△ADE和△ACB中,
即.又∠DAE=∠CAB,从而△ADE∽△ACB 因此∠ADE=∠ACB
所以C,B,D,E四点共圆。
(Ⅱ)m=4, n=6时,方程x2-14x+mn=0的两根为x1=2,x2=12.故 AD=2,AB=12.
取CE的中点G,DB的中点F,分别过G,F作AC,AB的垂线,两垂线相交于H点,连接DH.因为C,B,D,E四点共圆,所以C,B,D,E四点所在圆的圆心为H,半径为DH.
由于∠A=900,故GH∥AB, HF∥AC. HF=AG=5,DF= (12-2)=5.
故C,B,D,E四点所在圆的半径为5
23.解:(I)直线的参数方程是. -----------------(5分)
(II)因为点A,B都在直线l上,所以可设它们对应的参数为t1和t2,则点A,B的坐标分别为.
圆化为直角坐标系的方程.
以直线l的参数方程代入圆的方程整理得到
①
因为t1和t2是方程①的解,从而t1t2=-2.
所以|PA|·|PB|= |t1t2|=|-2|=2. -----------------(12分)
C1
昆明市五华区新世纪高级中学2012届高三第五次模拟考试题
理科数学
考试时间:2011年12月31日上午8:00-10:00,共120分钟 命题人:杨先明
题号 一 二 三 总分
得分
注意事项:
1.答题前,考生务必用黑色碳素笔将自己的姓名、考号、考场号、座位号等在答题卡上填写清楚,并认真核准。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案的标号。在试题卷上作答无效。
参考公式:
如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么 其中R表示球的半径
P(A·B)=P(A)·P(B) 球的体积公式
如果事件A在一次试验中发生的概率是
P,那么n次独立重复试验中恰好发生k次的概率 其中R表示球的半径
一、选择题(本大题共12小题,每小题5分,满分60分)
1.i为虚数单位,复平面内表示复数的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知集合,则=( )
A. B. C. D.
4.已知等比数列的公比为正数,且,则=( )
A. B. C. D.2
5.已知变量x、y满足的约束条件,则的最大值为( )
A.-3 B. C.-5 D.4
6.过点(0,1)且与曲线在点(3,2)处的切线垂直的直线的方程为( )
A. B. C. D.
7.为了得到函数的图像,只需把函数的图像( )
A.向左平移个长度单位 B.向右平移个长度单位
C.向左平移个长度单位 D.向右平移个长度单位
8.关于直线与平面,有以下四个命题:
①若,则 ②若
③若 ④若
其中真命题有( )
A.1个 B.2个 C.3个 D.4个
9. 若函数的导函数,则使得函数单调递减的一个充分不必要条件是x∈( )
A.[0,1] B.[3,5] C.[2,3] D.[2,4]
10.设若,则的值是( )
A. -1 B. 2 C. 1 D.-2
11.△ABC中,∠A=60°,∠A的平分线AD交边BC于D,已知AB=3,且,则AD的长为( )
A.1 B. C. D.3
12.在三棱锥S—ABC中,AB⊥BC,AB=BC=,SA=SC=2,,二面角S—AC—B的余弦值是,若S、A、B、C都在同一球面上,则该球的表面积是( )
A. B. C.24 D.6
二、填空题(本大题共4小题,每小题5分,共20分)
13. 在△ABC中,B=中,且,则△ABC的面积是_____
14. 某几何体的三视图如图所示,则它的体积是________.
15. 已知向量满足:,且,则向量与的夹角是 ___________.
16. 若等差数列的首项为,公差为,前n项的和为Sn,则数列为等差数列,且通项为.类似地,请完成下列命题:若各项均为正数的等比数列的首项为,公比为,前项的积为Tn,则 .
三、解答题(共5个小题,每小题12分,共60分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分12分)
设是公比大于1的等比数列,Sn为数列的前n项和.已知S3=7,且a1+3,3a2,a3+4构成等差数列.
(1)求数列的通项公式;
(2)令,求数列的前n项和Tn.
18. (本小题满分12分)
如图,在四棱锥A-ABCD中,底面ABCD是正方形,
其他四个侧面都是等边三角形,AC与BD的交点为O,
E为侧棱SC上一点.
(1)当E为侧棱SC的中点时,求证:SA∥平面BDE;
(2)求证:平面BDE⊥平面SAC;
(3)当二面角E-BD-C的大小为45°时,
试判断点E在SC上的位置,并说明理由.
19. (本小题满分12分)
已知锐角△ABC的三内角A、B、C的对边分别是a,b,c.且(b2+c2-a2)tanA=bc.
(1)求角A的大小;
(2)求的值.
20. (本小题满分12分)
如图,三棱柱ABC-A1B1C1的底面是边长为3的正三
角形,侧棱AA1垂直于底面ABC,AA1=,D是CB延
长线上一点,且BD=BC.
(1)求证:直线BC1∥平面AB1D;
(2)求二面角B1-AD-B的大小;
(3)求三棱锥C1-ABB1的体积。
21. (本小题满分12分)
已知函数.
(1)当且,时,试用含的式子表示,并讨论的单调区间;
(2)若有零点,,且对函数定义域内一切满足|x|≥2的实数x有≥0.
①求的表达式;
②当时,求函数的图象与函数的图象的交点坐标.
四、选考题(本小题满分10分)(请考生在22,23,24三题中任选一题做答,如果多做,则按所做的第一题记分.做答时用2B铅笔在答题卡把所选题目的题号涂黑)
23.选修4—4:坐标系与参数方程
以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线经过点P(1,1),倾斜角.
(1)写出直线的参数方程;
(2)设与圆相交于两点A、B,求点P到A、B两点的距离之积.
24.选修4—5:不等式选讲
已知函数f(x)=|2x-a|+a.
(1)若不等式f(x)≤6的解集为{x|-2≤x≤3},求实数a的值;
(2)在(1)的条件下,若存在实数n使f(n)≤m-f(-n)成立,求实数m的取值范围.
昆明市五华区新世纪高级中学2012届高三第五次模拟考试题
理科数学评分标准
一、选择题(12*5分=60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C D B B D A A B C C C D
二、填空题(4*5分=20分)
13、6 14.、 15、 16、
三、解答题(5*12分=60分)
17.解:(Ⅰ)设数列的公比为,
由已知,得 , ……………………………………2分
即, 也即
解得 ………………………………………………………………………5分
故数列的通项为. ………………………………………………6分
(Ⅱ)由(Ⅰ)得, ∴ , …………8分
又,
∴ 是以为首项,以为公差的等差数列 ……………10分
∴
即. ……………………………………………………………12分
18.证明:(Ⅰ)连接,由条件可得∥.
因为平面,平面,
所以∥平面.
(Ⅱ)法一:证明:由已知可得,,是中点,
所以,
又因为四边形是正方形,所以.
因为,所以
又因为,所以平面平面. -
(Ⅱ)法二:证明:由(Ⅰ)知,.
建立如图所示的空间直角坐标系.
设四棱锥的底面边长为2,
则,,,
,,.
所以,.
设(),由已知可求得.
所以,.
设平面法向量为,
则 即
令,得.
易知是平面的法向量.
因为,
所以,所以平面平面. -------------------(8分)
19.解:(1)由已知:
∴ ∴锐角△ABC ∴
(2)原式=
=
=
(Ⅱ)过作于,连结
平面,,
是二面角的平面角。
,是的中点,。
在中,
,即二面角的大小为60°
(Ⅲ)过作于,
平面,平面平面,
平面且为点到平面的距离。
,
。
21.解:(1) ………………2分
由,故
时 由 得的单调增区间是,
由 得单调减区间是
同理时,的单调增区间,,单调减区间为 …5分
(2)①由(1)及 (i)
又由 有知的零点在内,设,
则,结合(i)解得, …8分
∴ ………………9分
②又设,先求与轴在的交点
∵, 由 得
故,在单调递增
又,故与轴有唯一交点
即与的图象在区间上的唯一交点坐标为为所求 …………12分
四、选考题(10分)
22.
解析:(I)连接DE,根据题意在△ADE和△ACB中,
即.又∠DAE=∠CAB,从而△ADE∽△ACB 因此∠ADE=∠ACB
所以C,B,D,E四点共圆。
(Ⅱ)m=4, n=6时,方程x2-14x+mn=0的两根为x1=2,x2=12.故 AD=2,AB=12.
取CE的中点G,DB的中点F,分别过G,F作AC,AB的垂线,两垂线相交于H点,连接DH.因为C,B,D,E四点共圆,所以C,B,D,E四点所在圆的圆心为H,半径为DH.
由于∠A=900,故GH∥AB, HF∥AC. HF=AG=5,DF= (12-2)=5.
故C,B,D,E四点所在圆的半径为5
23.解:(I)直线的参数方程是. -----------------(5分)
(II)因为点A,B都在直线l上,所以可设它们对应的参数为t1和t2,则点A,B的坐标分别为.
圆化为直角坐标系的方程.
以直线l的参数方程代入圆的方程整理得到
①
因为t1和t2是方程①的解,从而t1t2=-2.
所以|PA|·|PB|= |t1t2|=|-2|=2. -----------------(12分)
C1
同课章节目录
