云南省昆明新世纪高级中学2012届高三第三次月考 文科数学试题
文档属性
| 名称 | 云南省昆明新世纪高级中学2012届高三第三次月考 文科数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 239.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-26 00:00:00 | ||
图片预览




文档简介
绝密★启用前
昆明市五华区新世纪高级中学2012届高三第三次模拟考试题
文科数学
考试时间:2011年10月28日上午8:00-10:00,共120分钟 命题人:李美鸯
题号 一 二 三 总分
得分
注意事项:
1.答题前,考生务必用黑色碳素笔将自己的姓名、考号、考场号、座位号等在答题卡上填写清楚,并认真核准。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案的标号。在试题卷上作答无效。
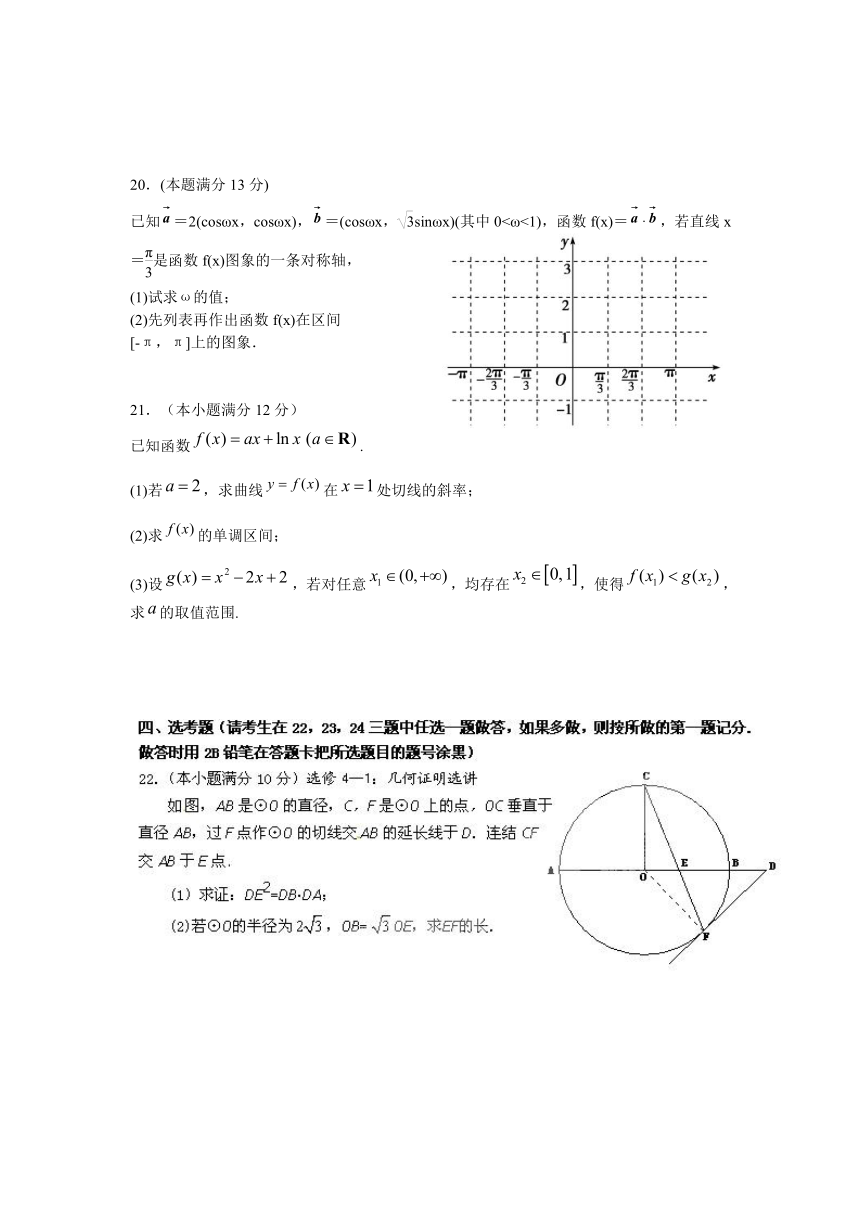
参考公式:
如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么 其中R表示球的半径
P(A·B)=P(A)·P(B) 球的体积公式
如果事件A在一次试验中发生的概率是
P,那么n次独立重复试验中恰好发生k次的概率 其中R表示球的半径
一、选择题(本大题共12小题,每小题5分,满分60分)
1.集合P={-1,0,1},Q={y|y=cos x,x∈R},则P∩Q=( )
A.P B.Q C.{-1,1} D.[0,1]
2. 若tan α=2,则的值为( )
A.0 B. C.1 D.
3.如图,函数f(x)的图象是曲线OAB,其中点O,A,B的
坐标分别为(0,0),(1,2),(3,1),则f()的值为( )
A. 1 B. 2 C.0 D.
4.向量,则“x=2”是“"的
A. 充分但不必要条件 B. 必要但不充分条件
C. 充要条件 D. 既不充分也不必要条件
5.简的结果是( )
A.-cos1 B.cos1 C.cos1 D.-cos1
6.函数(其中)的图象如图所示,为了得到
的图像,则只需将的图像( )
A.向右平移个长度单位
B.向右平移个长度单位
C.向左平移个长度单位 D.向左平移个长度单位
7.已知cos2α=,则sin2α=( )
A. B. C. D.
8.设函数则( )
A.在区间内均有零点 B.在区间内均无零点
C.在区间内有零点,在区间内无零点
D.在区间内无零点,在区间内有零点
9.已知O、A、B是平面上的三个点,直线AB上有一点C,满足2+=0,则=( )
A.2- B.-+2 C. - D.- +
10.曲线在点(1,1)处的切线为,则上的点到圆x2+y2+4x+3=0上的点的最近距离是( )
A. B. 2 C. D. 2
11. 若函数对定义域R内的任意都有=,且当时其导函数 满足若则( )
A. B.
C. D.
12.对于非零向量,定义运算“”:,其中为的夹角,有两两不共线的三个向量,下列结论正确的是( )
A.若,则 B.
C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
13.已知(2,3),=(-1,5),则=_________.
14.已知则的值为 .
15.已知函数,则满足不等式的x的范围是_________
16.已知向量与向量的夹角为120°,若向量,且,则的值为
________.
三、解答题(共5个小题,共60分,解答应写出文字说明,证明过程或演算步骤)
17.(本题满分10分)
已知命题p: x∈R,ax2+2x+3>0,如果命题¬p是真命题,那么实数a的取值范围
18.(本题满分12分)
如图某河段的两岸可视为平行,为了测量该河段的宽度,在河段的一岸边选取两点,观察对岸的点,测得, ,且米.
(1)求;
(2)求该河段的宽度.
19.(本题满分12分)
已知函数f(x)=x3-ax2+b(a,b为实数,且a>1)在区间[-1,1]上的最大值为1,最小值为-2.
(1)求f(x)的解析式;
(2)若函数g(x)=f(x)-mx在区间[-2,2]上为减函数,求实数m的取值范围.
20.(本题满分13分)
已知=2(cosωx,cosωx),=(cosωx,sinωx)(其中0<ω<1),函数f(x)=·,若直线x=是函数f(x)图象的一条对称轴,
(1)试求ω的值;
(2)先列表再作出函数f(x)在区间
[-π,π]上的图象.
21.(本小题满分12分)
已知函数.
(1)若,求曲线在处切线的斜率;
(2)求的单调区间;
(3)设,若对任意,均存在,使得,求的取值范围.
24.(本小题满分10分)选修4—5:不等式选讲
已知函数
(1)解关于的不等式;
(2)若函数的图象恒在函数图象的上方,求的取值范围。
昆明市五华区新世纪高级中学2012届高三第三次模拟考试题
文科数学评分标准
18.解:(1)
…3分
(2)∵,∴,
由正弦定理得:∴ …6分
如图过点作垂直于对岸,垂足为,则的长就是该河段的宽度。
在中,∵,
=(米)
∴该河段的宽度米。 …10分
19.本题满分12分
解:(1)f′(x)=3x2-3ax,
令f′(x)=0,得x1=0,x2=a,
∵a>1,
∴f(x)在[-1,0]上为增函数,在[0,1]上为减函数.
∴f(0)=b=1,
∵f (-1)=-a,f(1)=2-a,∴f(-1)∴f(-1)=-a=-2,a=.
∴f(x)=x3-2x2+1.
(2)g(x)=x3-2x2-mx+1,g′(x)=3x2-4x-m.
由g(x)在[-2,2]上为减函数,
知g′(x)≤0在x∈[-2,2]上恒成立.
∴,即∴m≥20.
∴实数m的取值范围是m≥20.
20.本题满分13分
解:f(x)=a·b=2(cosωx,cosωx)·(cosωx,sinωx)
=2cos2ωx+2cosωxsinωx
=1+cos2ωx+sin2ωx=1+2sin(2ωx+).
(1)∵直线x=为对称轴,∴sin(+)=±1,
∴+=kπ+(k∈Z).
∴ω=k+,∵0<ω<1,
∴-(2)由(1)知,f(x)=1+2sin(x+).
列表:
x+ -π - 0 π π
x -π -π - π
y 0 -1 1 3 1 0
描点作图,函数f(x)在[-π,π]上的图象如图所示.
21.解:(Ⅰ)由已知, ………………2分
.
故曲线在处切线的斜率为. ………………4分
(Ⅱ). ………………5分
①当时,由于,故,
所以,的单调递增区间为. ………………6分
②当时,由,得.
在区间上,,在区间上,
所以,函数的单调递增区间为,单调递减区间为.
………………7分
(Ⅲ)由已知,转化为. ………………8分
………………9分
由(Ⅱ)知,当时,在上单调递增,值域为,故不符合题意.
(或者举出反例:存在,故不符合题意.) ………………10分
当时,在上单调递增,在上单调递减,
故的极大值即为最大值,, ………11分
所以,解得. ………12分
22.(本小题满分10分)选修4—1:几何证明选讲
解:(Ⅰ)连结OF.∵DF切⊙O于F,
∴∠OFD=90°.∴∠OFC+∠CFD=90°.
∵OC=OF,∴∠OCF=∠OFC.
∵CO⊥AB于O,∴∠OCF+∠CEO=90°.
∴∠CFD=∠CEO=∠DEF,∴DF=DE.
∵DF是⊙O的切线,∴DF2=DB·DA.
∴DE2=DB·DA.---------------- ------------------5分
(Ⅱ),CO=, .
∵CE·EF= AE·EB= (+2)(-2)=8,∴EF=2.-----------------------10分
23.(本小题满分10分)选修4—4:坐标系与参数方程
解:(Ⅰ)的普通方程为,圆心,半径.………………1分
的普通方程为.………………2分
因为圆心到直线的距离为,………………4分
所以与只有一个公共点.………………5分
(Ⅱ)压缩后的参数方程分别为
:; :………………6分
化为普通方程为::,:,………………8分
联立消元得,其判别式,………9分
所以压缩后的直线与椭圆仍然只有一个公共点,和与公共点个数相同.…10分
昆明市五华区新世纪高级中学2012届高三第三次模拟考试题
文科数学
考试时间:2011年10月28日上午8:00-10:00,共120分钟 命题人:李美鸯
题号 一 二 三 总分
得分
注意事项:
1.答题前,考生务必用黑色碳素笔将自己的姓名、考号、考场号、座位号等在答题卡上填写清楚,并认真核准。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案的标号。在试题卷上作答无效。
参考公式:
如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么 其中R表示球的半径
P(A·B)=P(A)·P(B) 球的体积公式
如果事件A在一次试验中发生的概率是
P,那么n次独立重复试验中恰好发生k次的概率 其中R表示球的半径
一、选择题(本大题共12小题,每小题5分,满分60分)
1.集合P={-1,0,1},Q={y|y=cos x,x∈R},则P∩Q=( )
A.P B.Q C.{-1,1} D.[0,1]
2. 若tan α=2,则的值为( )
A.0 B. C.1 D.
3.如图,函数f(x)的图象是曲线OAB,其中点O,A,B的
坐标分别为(0,0),(1,2),(3,1),则f()的值为( )
A. 1 B. 2 C.0 D.
4.向量,则“x=2”是“"的
A. 充分但不必要条件 B. 必要但不充分条件
C. 充要条件 D. 既不充分也不必要条件
5.简的结果是( )
A.-cos1 B.cos1 C.cos1 D.-cos1
6.函数(其中)的图象如图所示,为了得到
的图像,则只需将的图像( )
A.向右平移个长度单位
B.向右平移个长度单位
C.向左平移个长度单位 D.向左平移个长度单位
7.已知cos2α=,则sin2α=( )
A. B. C. D.
8.设函数则( )
A.在区间内均有零点 B.在区间内均无零点
C.在区间内有零点,在区间内无零点
D.在区间内无零点,在区间内有零点
9.已知O、A、B是平面上的三个点,直线AB上有一点C,满足2+=0,则=( )
A.2- B.-+2 C. - D.- +
10.曲线在点(1,1)处的切线为,则上的点到圆x2+y2+4x+3=0上的点的最近距离是( )
A. B. 2 C. D. 2
11. 若函数对定义域R内的任意都有=,且当时其导函数 满足若则( )
A. B.
C. D.
12.对于非零向量,定义运算“”:,其中为的夹角,有两两不共线的三个向量,下列结论正确的是( )
A.若,则 B.
C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
13.已知(2,3),=(-1,5),则=_________.
14.已知则的值为 .
15.已知函数,则满足不等式的x的范围是_________
16.已知向量与向量的夹角为120°,若向量,且,则的值为
________.
三、解答题(共5个小题,共60分,解答应写出文字说明,证明过程或演算步骤)
17.(本题满分10分)
已知命题p: x∈R,ax2+2x+3>0,如果命题¬p是真命题,那么实数a的取值范围
18.(本题满分12分)
如图某河段的两岸可视为平行,为了测量该河段的宽度,在河段的一岸边选取两点,观察对岸的点,测得, ,且米.
(1)求;
(2)求该河段的宽度.
19.(本题满分12分)
已知函数f(x)=x3-ax2+b(a,b为实数,且a>1)在区间[-1,1]上的最大值为1,最小值为-2.
(1)求f(x)的解析式;
(2)若函数g(x)=f(x)-mx在区间[-2,2]上为减函数,求实数m的取值范围.
20.(本题满分13分)
已知=2(cosωx,cosωx),=(cosωx,sinωx)(其中0<ω<1),函数f(x)=·,若直线x=是函数f(x)图象的一条对称轴,
(1)试求ω的值;
(2)先列表再作出函数f(x)在区间
[-π,π]上的图象.
21.(本小题满分12分)
已知函数.
(1)若,求曲线在处切线的斜率;
(2)求的单调区间;
(3)设,若对任意,均存在,使得,求的取值范围.
24.(本小题满分10分)选修4—5:不等式选讲
已知函数
(1)解关于的不等式;
(2)若函数的图象恒在函数图象的上方,求的取值范围。
昆明市五华区新世纪高级中学2012届高三第三次模拟考试题
文科数学评分标准
18.解:(1)
…3分
(2)∵,∴,
由正弦定理得:∴ …6分
如图过点作垂直于对岸,垂足为,则的长就是该河段的宽度。
在中,∵,
=(米)
∴该河段的宽度米。 …10分
19.本题满分12分
解:(1)f′(x)=3x2-3ax,
令f′(x)=0,得x1=0,x2=a,
∵a>1,
∴f(x)在[-1,0]上为增函数,在[0,1]上为减函数.
∴f(0)=b=1,
∵f (-1)=-a,f(1)=2-a,∴f(-1)
∴f(x)=x3-2x2+1.
(2)g(x)=x3-2x2-mx+1,g′(x)=3x2-4x-m.
由g(x)在[-2,2]上为减函数,
知g′(x)≤0在x∈[-2,2]上恒成立.
∴,即∴m≥20.
∴实数m的取值范围是m≥20.
20.本题满分13分
解:f(x)=a·b=2(cosωx,cosωx)·(cosωx,sinωx)
=2cos2ωx+2cosωxsinωx
=1+cos2ωx+sin2ωx=1+2sin(2ωx+).
(1)∵直线x=为对称轴,∴sin(+)=±1,
∴+=kπ+(k∈Z).
∴ω=k+,∵0<ω<1,
∴-
列表:
x+ -π - 0 π π
x -π -π - π
y 0 -1 1 3 1 0
描点作图,函数f(x)在[-π,π]上的图象如图所示.
21.解:(Ⅰ)由已知, ………………2分
.
故曲线在处切线的斜率为. ………………4分
(Ⅱ). ………………5分
①当时,由于,故,
所以,的单调递增区间为. ………………6分
②当时,由,得.
在区间上,,在区间上,
所以,函数的单调递增区间为,单调递减区间为.
………………7分
(Ⅲ)由已知,转化为. ………………8分
………………9分
由(Ⅱ)知,当时,在上单调递增,值域为,故不符合题意.
(或者举出反例:存在,故不符合题意.) ………………10分
当时,在上单调递增,在上单调递减,
故的极大值即为最大值,, ………11分
所以,解得. ………12分
22.(本小题满分10分)选修4—1:几何证明选讲
解:(Ⅰ)连结OF.∵DF切⊙O于F,
∴∠OFD=90°.∴∠OFC+∠CFD=90°.
∵OC=OF,∴∠OCF=∠OFC.
∵CO⊥AB于O,∴∠OCF+∠CEO=90°.
∴∠CFD=∠CEO=∠DEF,∴DF=DE.
∵DF是⊙O的切线,∴DF2=DB·DA.
∴DE2=DB·DA.---------------- ------------------5分
(Ⅱ),CO=, .
∵CE·EF= AE·EB= (+2)(-2)=8,∴EF=2.-----------------------10分
23.(本小题满分10分)选修4—4:坐标系与参数方程
解:(Ⅰ)的普通方程为,圆心,半径.………………1分
的普通方程为.………………2分
因为圆心到直线的距离为,………………4分
所以与只有一个公共点.………………5分
(Ⅱ)压缩后的参数方程分别为
:; :………………6分
化为普通方程为::,:,………………8分
联立消元得,其判别式,………9分
所以压缩后的直线与椭圆仍然只有一个公共点,和与公共点个数相同.…10分
同课章节目录
