7.2坐标方法的简单应用-2020-2021学年人教版七年级数学下册导学案(含答案)
文档属性
| 名称 | 7.2坐标方法的简单应用-2020-2021学年人教版七年级数学下册导学案(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-23 00:00:00 | ||
图片预览


文档简介
7.1 平面直角坐标系
【总结解题方法 提升解题能力】
【知识点梳理】 一、用坐标表示地理位置
根据已知条件,建立适当的平面直角坐标系,是确定点的位置的必经过程,只有建立了适当的直角坐标系,点的位置才能得以确定,才能使数与形有机地结合在一起.利用平面直角坐标系绘制区域内一些地点分布情况的过程:
(1)建立坐标系,选择一个适当的参照点为原点,确定x轴,y轴的正方向;
(2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;
(3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.
二、用坐标表示平移
1、点的平移:
在平面直角坐标系中,将点(x,y)向右或向左平移a个单位长度,可以得到对应点(x+a,y)或(x-a,y);将点(x,y)向上或向下平移b个单位长度,可以得到对应点(x,y+b)或(x,y-b).
2、图形的平移:
在平面直角坐标系内,如果把一个图形各个点的横坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.
(1)横坐标变化,纵坐标不变:
原图形上的点(x,y)向右平移a个单位
原图形上的点(x,y)向左平移a个单位
(2)横坐标不变,纵坐标变化:
原图形上的点(x,y)向上平移b个单位
原图形上的点(x,y)向下平移b个单位
(3)横坐标、纵坐标都变化:
原图形上的点(x,y)向右平移a个单位,向上平移b个单位
原图形上的点(x,y)向右平移a个单位,向下平移b个单位
原图形上的点(x,y)向左平移a个单位,向上平移b个单位
原图形上的点(x,y)向左平移a个单位,向下平移b个单位
一、用坐标表示地理位置
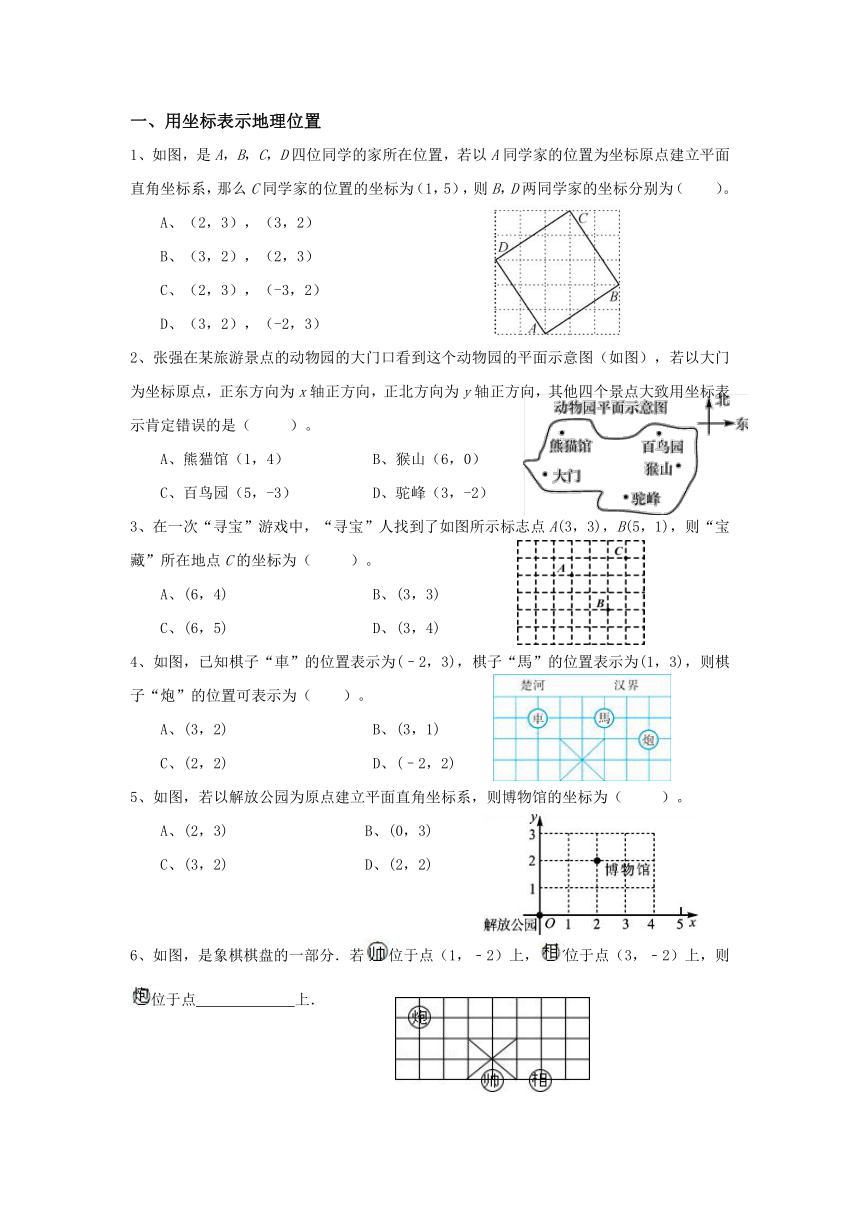
1、如图,是A,B,C,D四位同学的家所在位置,若以A同学家的位置为坐标原点建立平面直角坐标系,那么C同学家的位置的坐标为(1,5),则B,D两同学家的坐标分别为( )。
A、(2,3),(3,2)
B、(3,2),(2,3)
C、(2,3),(-3,2)
D、(3,2),(-2,3)
2、张强在某旅游景点的动物园的大门口看到这个动物园的平面示意图(如图),若以大门为坐标原点,正东方向为x轴正方向,正北方向为y轴正方向,其他四个景点大致用坐标表示肯定错误的是( )。
A、熊猫馆(1,4) B、猴山(6,0)
C、百鸟园(5,-3) D、驼峰(3,-2)
3、在一次“寻宝”游戏中,“寻宝”人找到了如图所示标志点A(3,3),B(5,1),则“宝藏”所在地点C的坐标为( )。
A、(6,4) B、(3,3)
C、(6,5) D、(3,4)
4、如图,已知棋子“車”的位置表示为(–2,3),棋子“馬”的位置表示为(1,3),则棋子“炮”的位置可表示为( )。
A、(3,2) B、(3,1)
C、(2,2) D、(–2,2)
5、如图,若以解放公园为原点建立平面直角坐标系,则博物馆的坐标为( )。
A、(2,3) B、(0,3)
C、(3,2) D、(2,2)
6、如图,是象棋棋盘的一部分.若位于点(1,﹣2)上,位于点(3,﹣2)上,则位于点 上.
7、如图是某学校的平面示意图.A,B,C,D,E,F分别表示学校的第1,2,3,4,5,6号楼.
(1)写出A,B,C,D,E的坐标;
(2)位于原点北偏东45°的是哪座楼,它的坐标是多少?
8、一个探险家在日记上记录了宝藏的位置,从海岛的一块大圆石O出发,向东1000m,向北1000m,向西500m,再向南750m,到达点P,即为宝藏的位置.
(1)画出坐标系确定宝藏的位置;
(2)确定点P的坐标.
9、如图是一所学校的平面示意图,已知国旗杆的坐标为(-1,1),写出其他几个建筑物位置的坐标.若国旗杆的坐标为(3,1),则其他几个建筑物位置的坐标是否发生改变?若改变,请写出坐标,若不改变,请说明理由.
二、用坐标表示平移
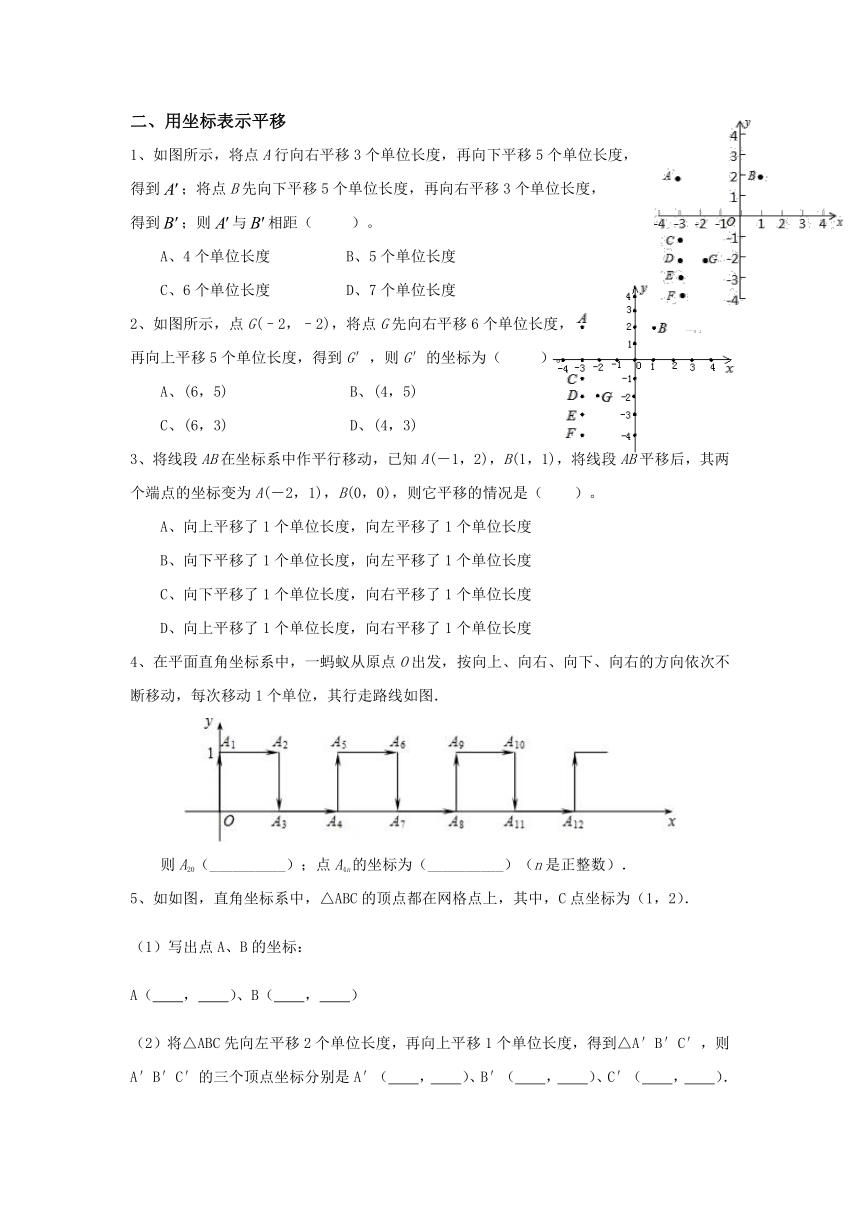
1、如图所示,将点A行向右平移3个单位长度,再向下平移5个单位长度,
得到;将点B先向下平移5个单位长度,再向右平移3个单位长度,
得到;则与相距( )。
A、4个单位长度 B、5个单位长度
C、6个单位长度 D、7个单位长度
2、如图所示,点G(–2,–2),将点G先向右平移6个单位长度,
再向上平移5个单位长度,得到G′,则G′的坐标为( )。
A、(6,5) B、(4,5)
C、(6,3) D、(4,3)
3、将线段AB在坐标系中作平行移动,已知A(-1,2),B(1,1),将线段AB平移后,其两个端点的坐标变为A(-2,1),B(0,0),则它平移的情况是( )。
A、向上平移了1个单位长度,向左平移了1个单位长度
B、向下平移了1个单位长度,向左平移了1个单位长度
C、向下平移了1个单位长度,向右平移了1个单位长度
D、向上平移了1个单位长度,向右平移了1个单位长度
4、在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图.
则A20(__________);点A4n的坐标为(__________)(n是正整数).
5、如如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
(1)写出点A、B的坐标:
A( , )、B( , )
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′( , )、B′( , )、C′( , ).
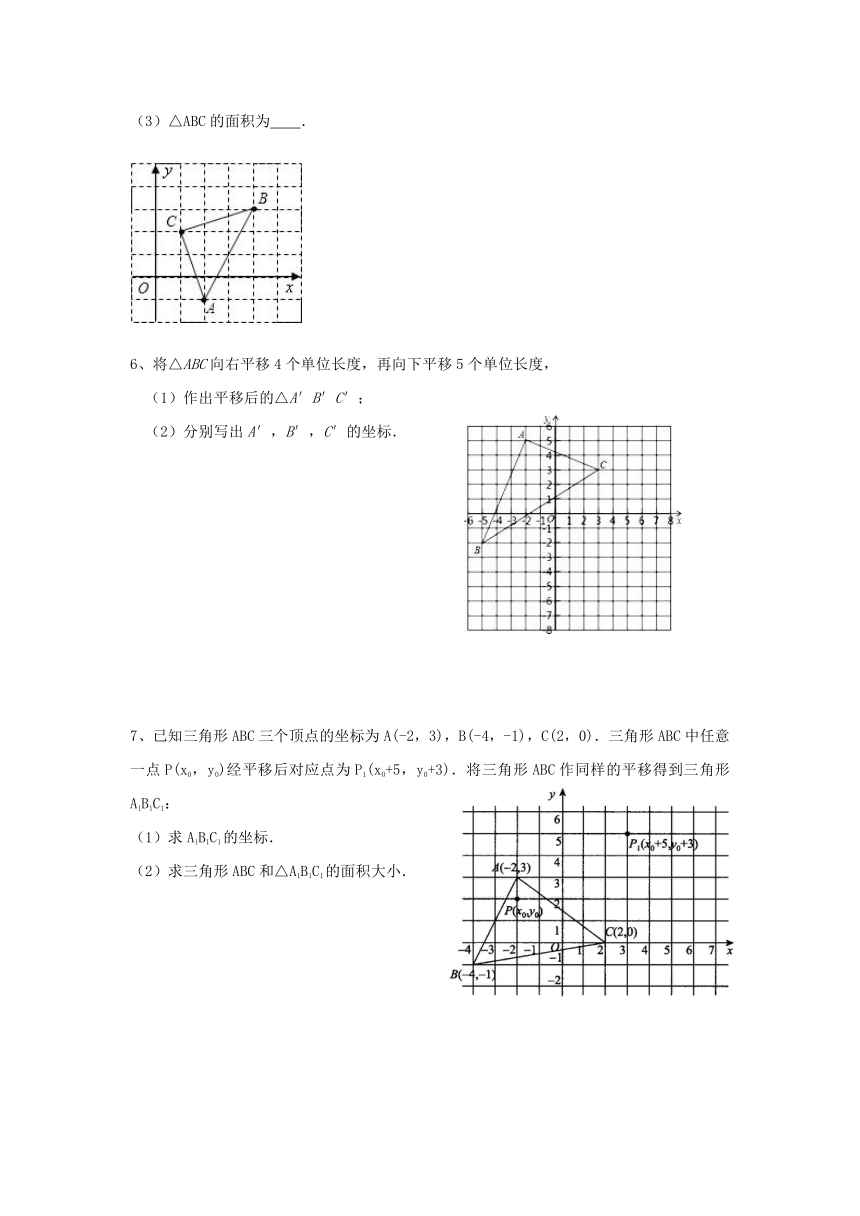
(3)△ABC的面积为 .
6、将△ABC向右平移4个单位长度,再向下平移5个单位长度,
(1)作出平移后的△A′B′C′;
(2)分别写出A′,B′,C′的坐标.
7、已知三角形ABC三个顶点的坐标为A(-2,3),B(-4,-1),C(2,0).三角形ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3).将三角形ABC作同样的平移得到三角形A1B1C1:
(1)求A1B1C1的坐标.
(2)求三角形ABC和△A1B1C1的面积大小.
【课后练习】
一、选择题
1、如图所示,某战役缴获敌人防御工事坐标地图碎片,依稀可见,一号暗堡的坐标为
(4,2),四号暗堡的坐标为(-2,4),原有情报得知:敌军指挥部的坐标为(0,0),你认为敌军指挥部的位置大约是( ).
A、A处 B、B处 C、C处 D、D处
2、某镇初级中学在镇政府的南偏西60°方向上,且距离镇政府1500m,则如图所示的表示法正确的是( ).
3、如图,将“笑脸”图标向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是( )。
A.(–1,6) B.(–9,6)
C.(–1,2) D.(–9,2)
4、已知△ABC顶点坐标分别是A(0,6),B(﹣3,﹣3),C(1,0),将△ABC平移后顶点A的对应点A1的坐标是(4,10),则点B的对应点B1的坐标为( )
A、(7,1) B、(1,7) C、(1,1) D、(2,1)
5、已知点A的坐标为(1,3),点B的坐标为(2,1).将线段AB沿某一方向平移后,点A的对应点的坐标为(–2,1),则点B的对应点的坐标为
A、(5,3) B、(–1,–2) C、(–1,–1) D、(0,–1)
6、课间操时,小明、小丽、小亮的位置如图所示,小明对小亮说:如果我的位置用(0,0)表示,小丽的位置用(2,1)表示,那么你的位置可以表示成( )。
A、(5,4) B、(4,5)
C、(3,4) D、(4,3)
7、中国象棋是中华民族的文化瑰宝,它源远流长,趣味性强,成为极其广泛的棋艺活动.如图,若在象棋盘上建立直角坐标系,使“帅”位于点(–1,–2),“马”位于点(3,–2),则“兵”位于点 ( )。
A、(–1,1) B、(–2,﹣1)
C、(–3,1) D、(–2,1)
8、如图,在平面直角坐标系中,三角形ABC位于第一象限,点A的坐标是(4,3),把三角形ABC向左平移6个单位长度,得到三角形A1B1C1,则点B1的坐标是( )。
A、(–2,3) B、(3,–1) C、(–3,1) D、(–5,2)
9、如图所示,△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),将B点向右平移2个单位长度后,再向上平移4个单位长度,到达B1点.若设△ABC的面积为S1,△AB1C的面积为S2,则S1,S2的大小关系为( ).
A.S1>S2 B.S1=S2 C.S1<S2 D.不能确定
10、如图所示,海上二救护中心收到一艘遇难船只的求救信号后,发现该船位于点A(5,-4),并且正以缓慢的速度向北漂移,同时发现在点B(5,2)和C(-1,-4)处各有一艘救护船.如果救护船的速度相同,问救护中心应派哪处的救护船前去救护可以在最短时间内靠近遇难船只? ( )
A、派C处 B、派B处
C、派C或B处 D、无法确定
二、填空题
11、某飞行监控中心发现某飞机从某个飞机场起飞后沿正南方向飞行100千米,然后向正西方向飞行300千米,又测得该机场的位置位于监控中心的西100千米,北300千米的地方,若以监控中心为坐标原点,以正东、正北方向为x轴、y轴的正方向,请指出该飞机现在的位置__________.(用坐标表示)
12、如图,一艘船在A处遇险后向相距50海里位于B处的救生船报警,用方向和距离描述遇险船相对于救生船的位置__________.
13、已知点A(a,5),B(2,2-b),C(4,2),且AB平行于x轴,AC平行于y轴,则a+b=__________.
14、在平面直角坐标系中,△A′B′C′是由△ABC平移后得到的,△ABC中任意一点P(x0,y0)经过平移后对应点为P′(x0+6,y0+1),若A′的坐标为(5,3),则它的对应的点A的坐标为__________.
15、如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为 .
16、在如图所示的平面直角坐标系中,一只蚂蚁从A点出发,沿着A-B-C-D-A-…循环爬行,其中A点坐标为(1,-1),B点坐标为(-1,-1),C点坐标为(-1,3),D点坐标为(1,3),当蚂蚁爬了2018个单位长度时,它所处位置的坐标为__________.
三、解答题
17、在直角坐标系中,△ABC的三个顶点的位置如图所示.
(1)请画出将△ABC先向右平移3个单位,再向上平移1个单位后得△A′B′C′,请在网格纸中画出△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′、B′、C′三点的坐标:A′_____,B′______,C′______.
18、如图,一条船从点O向北偏东37°方向航行2小时,走了50海里到达点A(30,40),然后以同样的速度向正东方向行进3小时,则船在什么位置?
19、如图所示的直角坐标系中,△ABC的顶点坐标分别是A(0,0),B(6,0),C(5,5).
(1)求△ABC的面积;
(2)如果将△ABC向上平移1个单位长度,得△A1B1C1,再向右平移2个单位长度,得到△A2B2C2,试求A2、B2、C2的坐标;
(3)△A2B2C2与△ABC的大小、形状有什么关系.
20、如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a﹣2|+(b﹣3)2=0,(c﹣4)2≤0
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.
参考答案
一、用坐标表示地理位置
1、如图,是A,B,C,D四位同学的家所在位置,若以A同学家的位置为坐标原点建立平面直角坐标系,那么C同学家的位置的坐标为(1,5),则B,D两同学家的坐标分别为( )。
A、(2,3),(3,2)
B、(3,2),(2,3)
C、(2,3),(-3,2)
D、(3,2),(-2,3)
【答案】D
【解析】建立平面直角坐标系如图,点B(3,2),D(?2,3),故选D.
2、张强在某旅游景点的动物园的大门口看到这个动物园的平面示意图(如图),若以大门为坐标原点,正东方向为x轴正方向,正北方向为y轴正方向,其他四个景点大致用坐标表示肯定错误的是( )。
A、熊猫馆(1,4) B、猴山(6,0)
C、百鸟园(5,-3) D、驼峰(3,-2)
【答案】C
【解析】若以大门为坐标原点建立直角坐标系,根据各点在坐标系中的位置及坐标的符号,可判定熊猫馆,猴山,百鸟园在第一象限,而驼峰在第四象限,观察各选项可知C选项百鸟园在第四象限,故C错误,故选C.
3、在一次“寻宝”游戏中,“寻宝”人找到了如图所示标志点A(3,3),B(5,1),则“宝藏”所在地点C的坐标为( )。
A、(6,4) B、(3,3)
C、(6,5) D、(3,4)
【答案】A
【解析】如图,根据点A(3,3),B(5,1)可确定如图所示的平面直角坐标系,所以点C的坐标为(6,4).
4、如图,已知棋子“車”的位置表示为(–2,3),棋子“馬”的位置表示为(1,3),则棋子“炮”的位置可表示为( )。
A、(3,2) B、(3,1)
C、(2,2) D、(–2,2)
【答案】A
【解析】棋子“车”的坐标为(–2,3),棋子“马”的坐标为(1,3),它们的纵坐标都是3,它们的横坐标分别为–2,1,可以确定棋子“炮”的坐标为(3,2).
5、如图,若以解放公园为原点建立平面直角坐标系,则博物馆的坐标为( )。
A、(2,3) B、(0,3)
C、(3,2) D、(2,2)
【答案】D
【解析】若以解放公园为原点建立平面直角坐标系,则博物馆的坐标为(2,2).故选D.
6、如图,是象棋棋盘的一部分.若位于点(1,﹣2)上,位于点(3,﹣2)上,则位于点 上.
【答案】(﹣2,1).
解:∵位于点(1,﹣2)上,位于点(3,﹣2)上,
∴位于点(﹣2,1)上.
7、如图是某学校的平面示意图.A,B,C,D,E,F分别表示学校的第1,2,3,4,5,6号楼.
(1)写出A,B,C,D,E的坐标;
(2)位于原点北偏东45°的是哪座楼,它的坐标是多少?
【解析】(1)根据平面直角坐标系得:
A(2,3),B(5,2),C(3,9),D(7,5),E(6,11).
(2)位于原点北偏东45°的点是点F,其坐标为(12,12).
8、一个探险家在日记上记录了宝藏的位置,从海岛的一块大圆石O出发,向东1000m,向北1000m,向西500m,再向南750m,到达点P,即为宝藏的位置.
(1)画出坐标系确定宝藏的位置;
(2)确定点P的坐标.
【解析】根据数据的特点,选择250作为单位长度,以大圆石O为原点,建立平面直角坐标系.
(1)如图,中心带有箭头的线是行动路线,点P的位置如图所示.
(2)点P的坐标是(500,250)
9、如图是一所学校的平面示意图,已知国旗杆的坐标为(-1,1),写出其他几个建筑物位置的坐标.若国旗杆的坐标为(3,1),则其他几个建筑物位置的坐标是否发生改变?若改变,请写出坐标,若不改变,请说明理由.
【解析】解:当国旗杆的坐标是(-1,1)时,校门的坐标是(-4,1),实验楼的坐标是(2,-2),教学楼的坐标是(2,1),图书馆的坐标是(1,4);若国旗杆的坐标是(3,1),则校门的坐标是(0,1),实验楼的坐标是(6,-2),教学楼的坐标是(6,1),图书馆的坐标是(5,4).
二、用坐标表示平移
1、如图所示,将点A行向右平移3个单位长度,再向下平移5个单位长度,
得到;将点B先向下平移5个单位长度,再向右平移3个单位长度,
得到;则与相距( )。
A、4个单位长度 B、5个单位长度
C、6个单位长度 D、7个单位长度
【答案】A
2、如图所示,点G(–2,–2),将点G先向右平移6个单位长度,
再向上平移5个单位长度,得到G′,则G′的坐标为( )。
A、(6,5) B、(4,5)
C、(6,3) D、(4,3)
【答案】D
【解析】本题主要考查了用坐标表示平移.注意左右移动改变点的横坐标,左减右加;上下移动改变点的纵坐标,下减上加.将点G先向右平移6个单位长度,即G′的横坐标为–2+6=4,再向上平移5个单位长度,即G′的纵坐标为–2+5=3,所以G′的坐标为(4,3),故选D.
3、将线段AB在坐标系中作平行移动,已知A(-1,2),B(1,1),将线段AB平移后,其两个端点的坐标变为A(-2,1),B(0,0),则它平移的情况是( )。
A、向上平移了1个单位长度,向左平移了1个单位长度
B、向下平移了1个单位长度,向左平移了1个单位长度
C、向下平移了1个单位长度,向右平移了1个单位长度
D、向上平移了1个单位长度,向右平移了1个单位长度
【答案】B
【解析】由点A,B的平移规律可知,此题规律是(x–1,y–1),照此规律可知线段AB向下平移了1个单位长度,向左平移了1个单位长度.故选B.
4、在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图.
则A20(__________);点A4n的坐标为(__________)(n是正整数).
【答案】10,0;2n,0.
【解析】观察发现,第4次跳动至点的坐标是(2,0),第8次跳动至点的坐标是(4,0),第12次跳动至点的坐标是(6,0),则第4n次跳动至点的坐标是(2n,0),故A20(10,0),故答案为:(10,0);(2n,0).
5、如如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
(1)写出点A、B的坐标:
A( , )、B( , )
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′( , )、B′( , )、C′( , ).
(3)△ABC的面积为 .
【解析】解:(1)写出点A、B的坐标:A(2,﹣1)、B(4,3)
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(0,0)、B′(2,4)、C′(﹣1,3).
(3)△ABC的面积=3×4﹣2××1×3﹣×2×4=5.
6、将△ABC向右平移4个单位长度,再向下平移5个单位长度,
(1)作出平移后的△A′B′C′;
(2)分别写出A′,B′,C′的坐标.
【解析】(1)如图:
(2)A′(2,0),B′(-1,-7),C′(7,-2).
7、已知三角形ABC三个顶点的坐标为A(-2,3),B(-4,-1),C(2,0).三角形ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3).将三角形ABC作同样的平移得到三角形A1B1C1:
(1)求A1B1C1的坐标.
(2)求三角形ABC和△A1B1C1的面积大小.
【解析】解:(1)A1(3,6),B1(1,2),C1(7,3).
(2)=24-4-3-6=11.
【课后练习】
一、选择题
1、如图所示,某战役缴获敌人防御工事坐标地图碎片,依稀可见,一号暗堡的坐标为
(4,2),四号暗堡的坐标为(-2,4),原有情报得知:敌军指挥部的坐标为(0,0),你认为敌军指挥部的位置大约是( ).
A、A处 B、B处 C、C处 D、D处
【答案】B;
【解析】根据点的坐标分为横坐标和纵坐标,横坐标是点到y轴的距离,纵坐标是点到x轴的距离,即可确定原点的位置.
2、某镇初级中学在镇政府的南偏西60°方向上,且距离镇政府1500m,则如图所示的表示法正确的是( ).
【答案】A;
3、如图,将“笑脸”图标向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是( )。
A.(–1,6) B.(–9,6)
C.(–1,2) D.(–9,2)
【答案】C
【解析】由题意P(–5,4),向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是(–1,2),故选C.
4、已知△ABC顶点坐标分别是A(0,6),B(﹣3,﹣3),C(1,0),将△ABC平移后顶点A的对应点A1的坐标是(4,10),则点B的对应点B1的坐标为( )
A、(7,1) B、(1,7) C、(1,1) D、(2,1)
【答案】C;
【解析】∵点A(0,6)平移后的对应点A1为(4,10),4﹣0=4,10﹣6=4,
∴△ABC向右平移了4个单位长度,向上平移了4个单位长度,
∴点B的对应点B1的坐标为(﹣3+4,﹣3+4),即(1,1).
5、已知点A的坐标为(1,3),点B的坐标为(2,1).将线段AB沿某一方向平移后,点A的对应点的坐标为(–2,1),则点B的对应点的坐标为
A、(5,3) B、(–1,–2) C、(–1,–1) D、(0,–1)
【答案】C
【解析】∵A(1,3)的对应点的坐标为(–2,1),∴平移规律为横坐标减3,纵坐标减2,
∵点B(2,1)的对应点的坐标为(–1,–1).故选C.
6、课间操时,小明、小丽、小亮的位置如图所示,小明对小亮说:如果我的位置用(0,0)表示,小丽的位置用(2,1)表示,那么你的位置可以表示成( )。
A、(5,4) B、(4,5)
C、(3,4) D、(4,3)
【答案】C
【解析】如果小明的位置用(0,0)表示,小丽的位置用(2,1)表示,
如图所示就是以小明为原点的平面直角坐标系,
所以小亮的位置为(3,4).故选C.
7、中国象棋是中华民族的文化瑰宝,它源远流长,趣味性强,成为极其广泛的棋艺活动.如图,若在象棋盘上建立直角坐标系,使“帅”位于点(–1,–2),“马”位于点(3,–2),则“兵”位于点 ( )。
A、(–1,1) B、(–2,﹣1)
C、(–3,1) D、(–2,1)
【答案】D
【解析】如图所示,根据题意可建立如图所示平面直角坐标系,
则“兵”位于点(–2,1),故选D.
8、如图,在平面直角坐标系中,三角形ABC位于第一象限,点A的坐标是(4,3),把三角形ABC向左平移6个单位长度,得到三角形A1B1C1,则点B1的坐标是( )。
A、(–2,3) B、(3,–1) C、(–3,1) D、(–5,2)
【答案】C
【解析】∵点B的坐标为(3,1),∴向左平移6个单位后,点B1的坐标(–3,1),
故选C.
9、如图所示,△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),将B点向右平移2个单位长度后,再向上平移4个单位长度,到达B1点.若设△ABC的面积为S1,△AB1C的面积为S2,则S1,S2的大小关系为( ).
A.S1>S2 B.S1=S2 C.S1<S2 D.不能确定
【答案】B;
【解析】解:△ABC的面积为S1=,将B点平移后得到B1点的坐标是(2,1),此时△AB1C的面积为S2=,所以S1=S2.故选B.
10、如图所示,海上二救护中心收到一艘遇难船只的求救信号后,发现该船位于点A(5,-4),并且正以缓慢的速度向北漂移,同时发现在点B(5,2)和C(-1,-4)处各有一艘救护船.如果救护船的速度相同,问救护中心应派哪处的救护船前去救护可以在最短时间内靠近遇难船只? ( )
A、派C处 B、派B处 C、派C或B处 D、无法确定
【答案】B.
二、填空题
11、某飞行监控中心发现某飞机从某个飞机场起飞后沿正南方向飞行100千米,然后向正西方向飞行300千米,又测得该机场的位置位于监控中心的西100千米,北300千米的地方,若以监控中心为坐标原点,以正东、正北方向为x轴、y轴的正方向,请指出该飞机现在的位置__________.(用坐标表示)
【答案】(-400,200)
【解析】该机场的位置位于监控中心的西100千米,北300千米的地方,若以监控中心为坐标原点,则机场的坐标为(-100,300),沿正南方向飞行100千米,然后向正西方向飞行300千米,则飞机现在的位置(-400,200),故答案:(-400,200).
12、如图,一艘船在A处遇险后向相距50海里位于B处的救生船报警,用方向和距离描述遇险船相对于救生船的位置__________.
【答案】南偏西15°,50海里
【解析】如图,内错角相等,所以A位于B,南偏西15°,50海里,故答案为:南偏西15°,50海里.
13、已知点A(a,5),B(2,2-b),C(4,2),且AB平行于x轴,AC平行于y轴,则a+b=__________.
【答案】1
【解析】因为AC平行于y轴,所以A,C两点的横坐标相同,即a=4.又AB平行于x轴,所以A,B两点的纵坐标相同,即2-b=5,所以b=-3.所以a+b=1,故答案为:1.
14、在平面直角坐标系中,△A′B′C′是由△ABC平移后得到的,△ABC中任意一点P(x0,y0)经过平移后对应点为P′(x0+6,y0+1),若A′的坐标为(5,3),则它的对应的点A的坐标为__________.
【答案】(-1,2)
【解析】根据题意,可得△ABC的平移规律为:向右平移6个单位,向上平移1个单位,∵A′的坐标为(5,3),∴它对应的点A的坐标为(?1,2),故答案为:(?1,2).
15、如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为 .
【答案】(1,3)或(5,1).
【解析】①如图1,当A平移到点C时,
∵C(3,2),A的坐标为(2,0),点B的坐标为(0,1),
∴点A的横坐标增大了1,纵坐标增大了2,平移后的B坐标为(1,3);
②如图2,当B平移到点C时,
∵C(3,2),A的坐标为(2,0),点B的坐标为(0,1),
∴点B的横坐标增大了3,纵坐标增大2,
∴平移后的A坐标为(5,1);
故答案为:(1,3)或(5,1).
16、在如图所示的平面直角坐标系中,一只蚂蚁从A点出发,沿着A-B-C-D-A-…循环爬行,其中A点坐标为(1,-1),B点坐标为(-1,-1),C点坐标为(-1,3),D点坐标为(1,3),当蚂蚁爬了2018个单位长度时,它所处位置的坐标为__________.
【答案】(-1,-1)
三、解答题
17、在直角坐标系中,△ABC的三个顶点的位置如图所示.
(1)请画出将△ABC先向右平移3个单位,再向上平移1个单位后得△A′B′C′,请在网格纸中画出△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′、B′、C′三点的坐标:A′_____,B′______,C′______.
【解析】(1)如图所示,△A′B′C′即为所求.
(2)A′(1,4),B′(0,2),C′(4,-1).
18、如图,一条船从点O向北偏东37°方向航行2小时,走了50海里到达点A(30,40),然后以同样的速度向正东方向行进3小时,则船在什么位置?
【解析】
解:船3小时后距A点为×3=75(海里),故A′(30+75,40),即A′(105,40).
所以船行进3小时后的位置是(105,40).
19、如图所示的直角坐标系中,△ABC的顶点坐标分别是A(0,0),B(6,0),C(5,5).
(1)求△ABC的面积;
(2)如果将△ABC向上平移1个单位长度,得△A1B1C1,再向右平移2个单位长度,得到△A2B2C2,试求A2、B2、C2的坐标;
(3)△A2B2C2与△ABC的大小、形状有什么关系.
【解析】解:(1)点C到x轴的距离为5,
所以;
(2)根据题意求出三角形A2B2C2各顶点的坐标为A2(2,1),B2(8,1),C2(7,6);
(3)连接A2B2C2三点可以看出△A2B2C2与△ABC的大小、形状相等或相同.
20、如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a﹣2|+(b﹣3)2=0,(c﹣4)2≤0
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.
【解析】解:(1)由已知|a﹣2|+(b﹣3)2=0,(c﹣4)2≤0及(c﹣4)2≥0
可得:a=2,b=3,c=4;
(2)∵×2×3=3,×2×(﹣m)=﹣m,
∴S四边形ABOP=S△ABO+S△APO=3+(﹣m)=3﹣m
(3)因为×4×3=6,
∵S四边形ABOP=S△ABC,∴3﹣m=6,
则 m=﹣3,
所以存在点P(﹣3,)使S四边形ABOP=S△ABC.
【总结解题方法 提升解题能力】
【知识点梳理】 一、用坐标表示地理位置
根据已知条件,建立适当的平面直角坐标系,是确定点的位置的必经过程,只有建立了适当的直角坐标系,点的位置才能得以确定,才能使数与形有机地结合在一起.利用平面直角坐标系绘制区域内一些地点分布情况的过程:
(1)建立坐标系,选择一个适当的参照点为原点,确定x轴,y轴的正方向;
(2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;
(3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.
二、用坐标表示平移
1、点的平移:
在平面直角坐标系中,将点(x,y)向右或向左平移a个单位长度,可以得到对应点(x+a,y)或(x-a,y);将点(x,y)向上或向下平移b个单位长度,可以得到对应点(x,y+b)或(x,y-b).
2、图形的平移:
在平面直角坐标系内,如果把一个图形各个点的横坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.
(1)横坐标变化,纵坐标不变:
原图形上的点(x,y)向右平移a个单位
原图形上的点(x,y)向左平移a个单位
(2)横坐标不变,纵坐标变化:
原图形上的点(x,y)向上平移b个单位
原图形上的点(x,y)向下平移b个单位
(3)横坐标、纵坐标都变化:
原图形上的点(x,y)向右平移a个单位,向上平移b个单位
原图形上的点(x,y)向右平移a个单位,向下平移b个单位
原图形上的点(x,y)向左平移a个单位,向上平移b个单位
原图形上的点(x,y)向左平移a个单位,向下平移b个单位
一、用坐标表示地理位置
1、如图,是A,B,C,D四位同学的家所在位置,若以A同学家的位置为坐标原点建立平面直角坐标系,那么C同学家的位置的坐标为(1,5),则B,D两同学家的坐标分别为( )。
A、(2,3),(3,2)
B、(3,2),(2,3)
C、(2,3),(-3,2)
D、(3,2),(-2,3)
2、张强在某旅游景点的动物园的大门口看到这个动物园的平面示意图(如图),若以大门为坐标原点,正东方向为x轴正方向,正北方向为y轴正方向,其他四个景点大致用坐标表示肯定错误的是( )。
A、熊猫馆(1,4) B、猴山(6,0)
C、百鸟园(5,-3) D、驼峰(3,-2)
3、在一次“寻宝”游戏中,“寻宝”人找到了如图所示标志点A(3,3),B(5,1),则“宝藏”所在地点C的坐标为( )。
A、(6,4) B、(3,3)
C、(6,5) D、(3,4)
4、如图,已知棋子“車”的位置表示为(–2,3),棋子“馬”的位置表示为(1,3),则棋子“炮”的位置可表示为( )。
A、(3,2) B、(3,1)
C、(2,2) D、(–2,2)
5、如图,若以解放公园为原点建立平面直角坐标系,则博物馆的坐标为( )。
A、(2,3) B、(0,3)
C、(3,2) D、(2,2)
6、如图,是象棋棋盘的一部分.若位于点(1,﹣2)上,位于点(3,﹣2)上,则位于点 上.
7、如图是某学校的平面示意图.A,B,C,D,E,F分别表示学校的第1,2,3,4,5,6号楼.
(1)写出A,B,C,D,E的坐标;
(2)位于原点北偏东45°的是哪座楼,它的坐标是多少?
8、一个探险家在日记上记录了宝藏的位置,从海岛的一块大圆石O出发,向东1000m,向北1000m,向西500m,再向南750m,到达点P,即为宝藏的位置.
(1)画出坐标系确定宝藏的位置;
(2)确定点P的坐标.
9、如图是一所学校的平面示意图,已知国旗杆的坐标为(-1,1),写出其他几个建筑物位置的坐标.若国旗杆的坐标为(3,1),则其他几个建筑物位置的坐标是否发生改变?若改变,请写出坐标,若不改变,请说明理由.
二、用坐标表示平移
1、如图所示,将点A行向右平移3个单位长度,再向下平移5个单位长度,
得到;将点B先向下平移5个单位长度,再向右平移3个单位长度,
得到;则与相距( )。
A、4个单位长度 B、5个单位长度
C、6个单位长度 D、7个单位长度
2、如图所示,点G(–2,–2),将点G先向右平移6个单位长度,
再向上平移5个单位长度,得到G′,则G′的坐标为( )。
A、(6,5) B、(4,5)
C、(6,3) D、(4,3)
3、将线段AB在坐标系中作平行移动,已知A(-1,2),B(1,1),将线段AB平移后,其两个端点的坐标变为A(-2,1),B(0,0),则它平移的情况是( )。
A、向上平移了1个单位长度,向左平移了1个单位长度
B、向下平移了1个单位长度,向左平移了1个单位长度
C、向下平移了1个单位长度,向右平移了1个单位长度
D、向上平移了1个单位长度,向右平移了1个单位长度
4、在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图.
则A20(__________);点A4n的坐标为(__________)(n是正整数).
5、如如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
(1)写出点A、B的坐标:
A( , )、B( , )
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′( , )、B′( , )、C′( , ).
(3)△ABC的面积为 .
6、将△ABC向右平移4个单位长度,再向下平移5个单位长度,
(1)作出平移后的△A′B′C′;
(2)分别写出A′,B′,C′的坐标.
7、已知三角形ABC三个顶点的坐标为A(-2,3),B(-4,-1),C(2,0).三角形ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3).将三角形ABC作同样的平移得到三角形A1B1C1:
(1)求A1B1C1的坐标.
(2)求三角形ABC和△A1B1C1的面积大小.
【课后练习】
一、选择题
1、如图所示,某战役缴获敌人防御工事坐标地图碎片,依稀可见,一号暗堡的坐标为
(4,2),四号暗堡的坐标为(-2,4),原有情报得知:敌军指挥部的坐标为(0,0),你认为敌军指挥部的位置大约是( ).
A、A处 B、B处 C、C处 D、D处
2、某镇初级中学在镇政府的南偏西60°方向上,且距离镇政府1500m,则如图所示的表示法正确的是( ).
3、如图,将“笑脸”图标向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是( )。
A.(–1,6) B.(–9,6)
C.(–1,2) D.(–9,2)
4、已知△ABC顶点坐标分别是A(0,6),B(﹣3,﹣3),C(1,0),将△ABC平移后顶点A的对应点A1的坐标是(4,10),则点B的对应点B1的坐标为( )
A、(7,1) B、(1,7) C、(1,1) D、(2,1)
5、已知点A的坐标为(1,3),点B的坐标为(2,1).将线段AB沿某一方向平移后,点A的对应点的坐标为(–2,1),则点B的对应点的坐标为
A、(5,3) B、(–1,–2) C、(–1,–1) D、(0,–1)
6、课间操时,小明、小丽、小亮的位置如图所示,小明对小亮说:如果我的位置用(0,0)表示,小丽的位置用(2,1)表示,那么你的位置可以表示成( )。
A、(5,4) B、(4,5)
C、(3,4) D、(4,3)
7、中国象棋是中华民族的文化瑰宝,它源远流长,趣味性强,成为极其广泛的棋艺活动.如图,若在象棋盘上建立直角坐标系,使“帅”位于点(–1,–2),“马”位于点(3,–2),则“兵”位于点 ( )。
A、(–1,1) B、(–2,﹣1)
C、(–3,1) D、(–2,1)
8、如图,在平面直角坐标系中,三角形ABC位于第一象限,点A的坐标是(4,3),把三角形ABC向左平移6个单位长度,得到三角形A1B1C1,则点B1的坐标是( )。
A、(–2,3) B、(3,–1) C、(–3,1) D、(–5,2)
9、如图所示,△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),将B点向右平移2个单位长度后,再向上平移4个单位长度,到达B1点.若设△ABC的面积为S1,△AB1C的面积为S2,则S1,S2的大小关系为( ).
A.S1>S2 B.S1=S2 C.S1<S2 D.不能确定
10、如图所示,海上二救护中心收到一艘遇难船只的求救信号后,发现该船位于点A(5,-4),并且正以缓慢的速度向北漂移,同时发现在点B(5,2)和C(-1,-4)处各有一艘救护船.如果救护船的速度相同,问救护中心应派哪处的救护船前去救护可以在最短时间内靠近遇难船只? ( )
A、派C处 B、派B处
C、派C或B处 D、无法确定
二、填空题
11、某飞行监控中心发现某飞机从某个飞机场起飞后沿正南方向飞行100千米,然后向正西方向飞行300千米,又测得该机场的位置位于监控中心的西100千米,北300千米的地方,若以监控中心为坐标原点,以正东、正北方向为x轴、y轴的正方向,请指出该飞机现在的位置__________.(用坐标表示)
12、如图,一艘船在A处遇险后向相距50海里位于B处的救生船报警,用方向和距离描述遇险船相对于救生船的位置__________.
13、已知点A(a,5),B(2,2-b),C(4,2),且AB平行于x轴,AC平行于y轴,则a+b=__________.
14、在平面直角坐标系中,△A′B′C′是由△ABC平移后得到的,△ABC中任意一点P(x0,y0)经过平移后对应点为P′(x0+6,y0+1),若A′的坐标为(5,3),则它的对应的点A的坐标为__________.
15、如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为 .
16、在如图所示的平面直角坐标系中,一只蚂蚁从A点出发,沿着A-B-C-D-A-…循环爬行,其中A点坐标为(1,-1),B点坐标为(-1,-1),C点坐标为(-1,3),D点坐标为(1,3),当蚂蚁爬了2018个单位长度时,它所处位置的坐标为__________.
三、解答题
17、在直角坐标系中,△ABC的三个顶点的位置如图所示.
(1)请画出将△ABC先向右平移3个单位,再向上平移1个单位后得△A′B′C′,请在网格纸中画出△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′、B′、C′三点的坐标:A′_____,B′______,C′______.
18、如图,一条船从点O向北偏东37°方向航行2小时,走了50海里到达点A(30,40),然后以同样的速度向正东方向行进3小时,则船在什么位置?
19、如图所示的直角坐标系中,△ABC的顶点坐标分别是A(0,0),B(6,0),C(5,5).
(1)求△ABC的面积;
(2)如果将△ABC向上平移1个单位长度,得△A1B1C1,再向右平移2个单位长度,得到△A2B2C2,试求A2、B2、C2的坐标;
(3)△A2B2C2与△ABC的大小、形状有什么关系.
20、如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a﹣2|+(b﹣3)2=0,(c﹣4)2≤0
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.
参考答案
一、用坐标表示地理位置
1、如图,是A,B,C,D四位同学的家所在位置,若以A同学家的位置为坐标原点建立平面直角坐标系,那么C同学家的位置的坐标为(1,5),则B,D两同学家的坐标分别为( )。
A、(2,3),(3,2)
B、(3,2),(2,3)
C、(2,3),(-3,2)
D、(3,2),(-2,3)
【答案】D
【解析】建立平面直角坐标系如图,点B(3,2),D(?2,3),故选D.
2、张强在某旅游景点的动物园的大门口看到这个动物园的平面示意图(如图),若以大门为坐标原点,正东方向为x轴正方向,正北方向为y轴正方向,其他四个景点大致用坐标表示肯定错误的是( )。
A、熊猫馆(1,4) B、猴山(6,0)
C、百鸟园(5,-3) D、驼峰(3,-2)
【答案】C
【解析】若以大门为坐标原点建立直角坐标系,根据各点在坐标系中的位置及坐标的符号,可判定熊猫馆,猴山,百鸟园在第一象限,而驼峰在第四象限,观察各选项可知C选项百鸟园在第四象限,故C错误,故选C.
3、在一次“寻宝”游戏中,“寻宝”人找到了如图所示标志点A(3,3),B(5,1),则“宝藏”所在地点C的坐标为( )。
A、(6,4) B、(3,3)
C、(6,5) D、(3,4)
【答案】A
【解析】如图,根据点A(3,3),B(5,1)可确定如图所示的平面直角坐标系,所以点C的坐标为(6,4).
4、如图,已知棋子“車”的位置表示为(–2,3),棋子“馬”的位置表示为(1,3),则棋子“炮”的位置可表示为( )。
A、(3,2) B、(3,1)
C、(2,2) D、(–2,2)
【答案】A
【解析】棋子“车”的坐标为(–2,3),棋子“马”的坐标为(1,3),它们的纵坐标都是3,它们的横坐标分别为–2,1,可以确定棋子“炮”的坐标为(3,2).
5、如图,若以解放公园为原点建立平面直角坐标系,则博物馆的坐标为( )。
A、(2,3) B、(0,3)
C、(3,2) D、(2,2)
【答案】D
【解析】若以解放公园为原点建立平面直角坐标系,则博物馆的坐标为(2,2).故选D.
6、如图,是象棋棋盘的一部分.若位于点(1,﹣2)上,位于点(3,﹣2)上,则位于点 上.
【答案】(﹣2,1).
解:∵位于点(1,﹣2)上,位于点(3,﹣2)上,
∴位于点(﹣2,1)上.
7、如图是某学校的平面示意图.A,B,C,D,E,F分别表示学校的第1,2,3,4,5,6号楼.
(1)写出A,B,C,D,E的坐标;
(2)位于原点北偏东45°的是哪座楼,它的坐标是多少?
【解析】(1)根据平面直角坐标系得:
A(2,3),B(5,2),C(3,9),D(7,5),E(6,11).
(2)位于原点北偏东45°的点是点F,其坐标为(12,12).
8、一个探险家在日记上记录了宝藏的位置,从海岛的一块大圆石O出发,向东1000m,向北1000m,向西500m,再向南750m,到达点P,即为宝藏的位置.
(1)画出坐标系确定宝藏的位置;
(2)确定点P的坐标.
【解析】根据数据的特点,选择250作为单位长度,以大圆石O为原点,建立平面直角坐标系.
(1)如图,中心带有箭头的线是行动路线,点P的位置如图所示.
(2)点P的坐标是(500,250)
9、如图是一所学校的平面示意图,已知国旗杆的坐标为(-1,1),写出其他几个建筑物位置的坐标.若国旗杆的坐标为(3,1),则其他几个建筑物位置的坐标是否发生改变?若改变,请写出坐标,若不改变,请说明理由.
【解析】解:当国旗杆的坐标是(-1,1)时,校门的坐标是(-4,1),实验楼的坐标是(2,-2),教学楼的坐标是(2,1),图书馆的坐标是(1,4);若国旗杆的坐标是(3,1),则校门的坐标是(0,1),实验楼的坐标是(6,-2),教学楼的坐标是(6,1),图书馆的坐标是(5,4).
二、用坐标表示平移
1、如图所示,将点A行向右平移3个单位长度,再向下平移5个单位长度,
得到;将点B先向下平移5个单位长度,再向右平移3个单位长度,
得到;则与相距( )。
A、4个单位长度 B、5个单位长度
C、6个单位长度 D、7个单位长度
【答案】A
2、如图所示,点G(–2,–2),将点G先向右平移6个单位长度,
再向上平移5个单位长度,得到G′,则G′的坐标为( )。
A、(6,5) B、(4,5)
C、(6,3) D、(4,3)
【答案】D
【解析】本题主要考查了用坐标表示平移.注意左右移动改变点的横坐标,左减右加;上下移动改变点的纵坐标,下减上加.将点G先向右平移6个单位长度,即G′的横坐标为–2+6=4,再向上平移5个单位长度,即G′的纵坐标为–2+5=3,所以G′的坐标为(4,3),故选D.
3、将线段AB在坐标系中作平行移动,已知A(-1,2),B(1,1),将线段AB平移后,其两个端点的坐标变为A(-2,1),B(0,0),则它平移的情况是( )。
A、向上平移了1个单位长度,向左平移了1个单位长度
B、向下平移了1个单位长度,向左平移了1个单位长度
C、向下平移了1个单位长度,向右平移了1个单位长度
D、向上平移了1个单位长度,向右平移了1个单位长度
【答案】B
【解析】由点A,B的平移规律可知,此题规律是(x–1,y–1),照此规律可知线段AB向下平移了1个单位长度,向左平移了1个单位长度.故选B.
4、在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图.
则A20(__________);点A4n的坐标为(__________)(n是正整数).
【答案】10,0;2n,0.
【解析】观察发现,第4次跳动至点的坐标是(2,0),第8次跳动至点的坐标是(4,0),第12次跳动至点的坐标是(6,0),则第4n次跳动至点的坐标是(2n,0),故A20(10,0),故答案为:(10,0);(2n,0).
5、如如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
(1)写出点A、B的坐标:
A( , )、B( , )
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′( , )、B′( , )、C′( , ).
(3)△ABC的面积为 .
【解析】解:(1)写出点A、B的坐标:A(2,﹣1)、B(4,3)
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(0,0)、B′(2,4)、C′(﹣1,3).
(3)△ABC的面积=3×4﹣2××1×3﹣×2×4=5.
6、将△ABC向右平移4个单位长度,再向下平移5个单位长度,
(1)作出平移后的△A′B′C′;
(2)分别写出A′,B′,C′的坐标.
【解析】(1)如图:
(2)A′(2,0),B′(-1,-7),C′(7,-2).
7、已知三角形ABC三个顶点的坐标为A(-2,3),B(-4,-1),C(2,0).三角形ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3).将三角形ABC作同样的平移得到三角形A1B1C1:
(1)求A1B1C1的坐标.
(2)求三角形ABC和△A1B1C1的面积大小.
【解析】解:(1)A1(3,6),B1(1,2),C1(7,3).
(2)=24-4-3-6=11.
【课后练习】
一、选择题
1、如图所示,某战役缴获敌人防御工事坐标地图碎片,依稀可见,一号暗堡的坐标为
(4,2),四号暗堡的坐标为(-2,4),原有情报得知:敌军指挥部的坐标为(0,0),你认为敌军指挥部的位置大约是( ).
A、A处 B、B处 C、C处 D、D处
【答案】B;
【解析】根据点的坐标分为横坐标和纵坐标,横坐标是点到y轴的距离,纵坐标是点到x轴的距离,即可确定原点的位置.
2、某镇初级中学在镇政府的南偏西60°方向上,且距离镇政府1500m,则如图所示的表示法正确的是( ).
【答案】A;
3、如图,将“笑脸”图标向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是( )。
A.(–1,6) B.(–9,6)
C.(–1,2) D.(–9,2)
【答案】C
【解析】由题意P(–5,4),向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是(–1,2),故选C.
4、已知△ABC顶点坐标分别是A(0,6),B(﹣3,﹣3),C(1,0),将△ABC平移后顶点A的对应点A1的坐标是(4,10),则点B的对应点B1的坐标为( )
A、(7,1) B、(1,7) C、(1,1) D、(2,1)
【答案】C;
【解析】∵点A(0,6)平移后的对应点A1为(4,10),4﹣0=4,10﹣6=4,
∴△ABC向右平移了4个单位长度,向上平移了4个单位长度,
∴点B的对应点B1的坐标为(﹣3+4,﹣3+4),即(1,1).
5、已知点A的坐标为(1,3),点B的坐标为(2,1).将线段AB沿某一方向平移后,点A的对应点的坐标为(–2,1),则点B的对应点的坐标为
A、(5,3) B、(–1,–2) C、(–1,–1) D、(0,–1)
【答案】C
【解析】∵A(1,3)的对应点的坐标为(–2,1),∴平移规律为横坐标减3,纵坐标减2,
∵点B(2,1)的对应点的坐标为(–1,–1).故选C.
6、课间操时,小明、小丽、小亮的位置如图所示,小明对小亮说:如果我的位置用(0,0)表示,小丽的位置用(2,1)表示,那么你的位置可以表示成( )。
A、(5,4) B、(4,5)
C、(3,4) D、(4,3)
【答案】C
【解析】如果小明的位置用(0,0)表示,小丽的位置用(2,1)表示,
如图所示就是以小明为原点的平面直角坐标系,
所以小亮的位置为(3,4).故选C.
7、中国象棋是中华民族的文化瑰宝,它源远流长,趣味性强,成为极其广泛的棋艺活动.如图,若在象棋盘上建立直角坐标系,使“帅”位于点(–1,–2),“马”位于点(3,–2),则“兵”位于点 ( )。
A、(–1,1) B、(–2,﹣1)
C、(–3,1) D、(–2,1)
【答案】D
【解析】如图所示,根据题意可建立如图所示平面直角坐标系,
则“兵”位于点(–2,1),故选D.
8、如图,在平面直角坐标系中,三角形ABC位于第一象限,点A的坐标是(4,3),把三角形ABC向左平移6个单位长度,得到三角形A1B1C1,则点B1的坐标是( )。
A、(–2,3) B、(3,–1) C、(–3,1) D、(–5,2)
【答案】C
【解析】∵点B的坐标为(3,1),∴向左平移6个单位后,点B1的坐标(–3,1),
故选C.
9、如图所示,△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),将B点向右平移2个单位长度后,再向上平移4个单位长度,到达B1点.若设△ABC的面积为S1,△AB1C的面积为S2,则S1,S2的大小关系为( ).
A.S1>S2 B.S1=S2 C.S1<S2 D.不能确定
【答案】B;
【解析】解:△ABC的面积为S1=,将B点平移后得到B1点的坐标是(2,1),此时△AB1C的面积为S2=,所以S1=S2.故选B.
10、如图所示,海上二救护中心收到一艘遇难船只的求救信号后,发现该船位于点A(5,-4),并且正以缓慢的速度向北漂移,同时发现在点B(5,2)和C(-1,-4)处各有一艘救护船.如果救护船的速度相同,问救护中心应派哪处的救护船前去救护可以在最短时间内靠近遇难船只? ( )
A、派C处 B、派B处 C、派C或B处 D、无法确定
【答案】B.
二、填空题
11、某飞行监控中心发现某飞机从某个飞机场起飞后沿正南方向飞行100千米,然后向正西方向飞行300千米,又测得该机场的位置位于监控中心的西100千米,北300千米的地方,若以监控中心为坐标原点,以正东、正北方向为x轴、y轴的正方向,请指出该飞机现在的位置__________.(用坐标表示)
【答案】(-400,200)
【解析】该机场的位置位于监控中心的西100千米,北300千米的地方,若以监控中心为坐标原点,则机场的坐标为(-100,300),沿正南方向飞行100千米,然后向正西方向飞行300千米,则飞机现在的位置(-400,200),故答案:(-400,200).
12、如图,一艘船在A处遇险后向相距50海里位于B处的救生船报警,用方向和距离描述遇险船相对于救生船的位置__________.
【答案】南偏西15°,50海里
【解析】如图,内错角相等,所以A位于B,南偏西15°,50海里,故答案为:南偏西15°,50海里.
13、已知点A(a,5),B(2,2-b),C(4,2),且AB平行于x轴,AC平行于y轴,则a+b=__________.
【答案】1
【解析】因为AC平行于y轴,所以A,C两点的横坐标相同,即a=4.又AB平行于x轴,所以A,B两点的纵坐标相同,即2-b=5,所以b=-3.所以a+b=1,故答案为:1.
14、在平面直角坐标系中,△A′B′C′是由△ABC平移后得到的,△ABC中任意一点P(x0,y0)经过平移后对应点为P′(x0+6,y0+1),若A′的坐标为(5,3),则它的对应的点A的坐标为__________.
【答案】(-1,2)
【解析】根据题意,可得△ABC的平移规律为:向右平移6个单位,向上平移1个单位,∵A′的坐标为(5,3),∴它对应的点A的坐标为(?1,2),故答案为:(?1,2).
15、如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为 .
【答案】(1,3)或(5,1).
【解析】①如图1,当A平移到点C时,
∵C(3,2),A的坐标为(2,0),点B的坐标为(0,1),
∴点A的横坐标增大了1,纵坐标增大了2,平移后的B坐标为(1,3);
②如图2,当B平移到点C时,
∵C(3,2),A的坐标为(2,0),点B的坐标为(0,1),
∴点B的横坐标增大了3,纵坐标增大2,
∴平移后的A坐标为(5,1);
故答案为:(1,3)或(5,1).
16、在如图所示的平面直角坐标系中,一只蚂蚁从A点出发,沿着A-B-C-D-A-…循环爬行,其中A点坐标为(1,-1),B点坐标为(-1,-1),C点坐标为(-1,3),D点坐标为(1,3),当蚂蚁爬了2018个单位长度时,它所处位置的坐标为__________.
【答案】(-1,-1)
三、解答题
17、在直角坐标系中,△ABC的三个顶点的位置如图所示.
(1)请画出将△ABC先向右平移3个单位,再向上平移1个单位后得△A′B′C′,请在网格纸中画出△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′、B′、C′三点的坐标:A′_____,B′______,C′______.
【解析】(1)如图所示,△A′B′C′即为所求.
(2)A′(1,4),B′(0,2),C′(4,-1).
18、如图,一条船从点O向北偏东37°方向航行2小时,走了50海里到达点A(30,40),然后以同样的速度向正东方向行进3小时,则船在什么位置?
【解析】
解:船3小时后距A点为×3=75(海里),故A′(30+75,40),即A′(105,40).
所以船行进3小时后的位置是(105,40).
19、如图所示的直角坐标系中,△ABC的顶点坐标分别是A(0,0),B(6,0),C(5,5).
(1)求△ABC的面积;
(2)如果将△ABC向上平移1个单位长度,得△A1B1C1,再向右平移2个单位长度,得到△A2B2C2,试求A2、B2、C2的坐标;
(3)△A2B2C2与△ABC的大小、形状有什么关系.
【解析】解:(1)点C到x轴的距离为5,
所以;
(2)根据题意求出三角形A2B2C2各顶点的坐标为A2(2,1),B2(8,1),C2(7,6);
(3)连接A2B2C2三点可以看出△A2B2C2与△ABC的大小、形状相等或相同.
20、如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a﹣2|+(b﹣3)2=0,(c﹣4)2≤0
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.
【解析】解:(1)由已知|a﹣2|+(b﹣3)2=0,(c﹣4)2≤0及(c﹣4)2≥0
可得:a=2,b=3,c=4;
(2)∵×2×3=3,×2×(﹣m)=﹣m,
∴S四边形ABOP=S△ABO+S△APO=3+(﹣m)=3﹣m
(3)因为×4×3=6,
∵S四边形ABOP=S△ABC,∴3﹣m=6,
则 m=﹣3,
所以存在点P(﹣3,)使S四边形ABOP=S△ABC.
