8.3 实际问题与二元一次方程组 (工作量问题) 教案2020-2021学年人教版七年级数学下册(表格式)
文档属性
| 名称 | 8.3 实际问题与二元一次方程组 (工作量问题) 教案2020-2021学年人教版七年级数学下册(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 53.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 00:00:00 | ||
图片预览

文档简介
教师姓名
单位名称
填写时间
学科 数学 年级/册 七年级(下) 教材版本 人教版
课题名称 第八章 二元一次方程组与实际问题(工作量问题)
教学目标
课标要求:建立方程模型,运用方程解决实际问题,体会方程是刻划现实世界的有效数学模型。
1.会用二元一次方程组解决“探究2”提出的问题.
2.通过思考、讨论、探究事物之间数量关系,建立方程模型,运用方程解决实际问题,体会方程是刻划现实世界的有效数学模型。
3.通过对实际问题的解决,培养学生应用方程的意识,从而提高学生对数学趣味性、现实性、科学性的认识.
重、难点 教学重点 让学生实践与探索,运用二元一次方程解决有关配套与设计问题
教学难点 寻找关键词,列出等量关系.
难点分析 从知识角度分析为什么难 解决实际问题要首先通过设未知数正确找到问题中的两个等量关系,进而建立模型将生活中的实际问题转化为数学问题,通过对数学问题的解答达到解决实际问题的目的。
从学生角度分析为什么难 学生不能正确找出等量关系式,列出方程组
难点教学方法
通过审题、找等量关系,列出方程组。
教学环节
教学过程
导入 上节课我们初步体验了用方程组解决实际问题的全过程,其实生产,生活中还有许多问题也能用方程组解决.
今天,我们再来看研究一个实际生活中的例子。
如何将实际问题转化为数学问题进行解答?
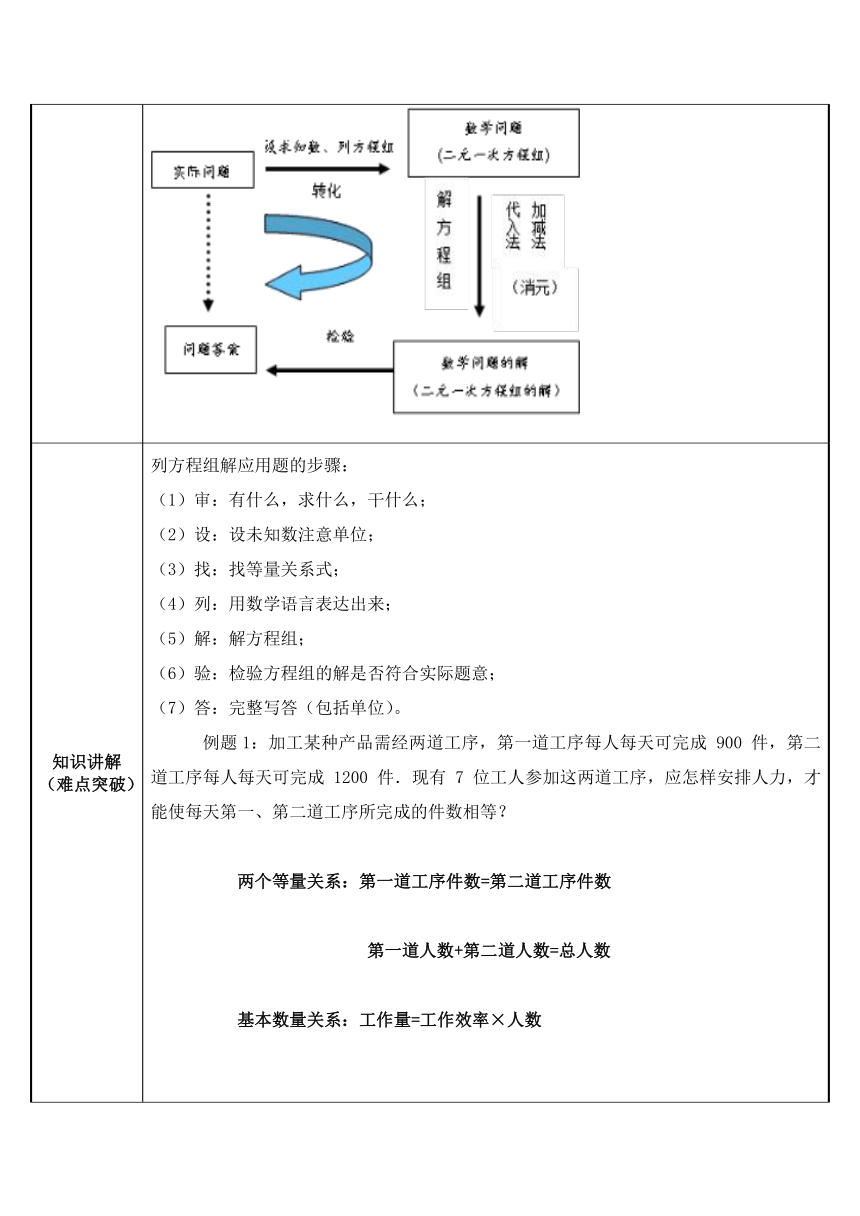
知识讲解 (难点突破) 列方程组解应用题的步骤:
审:有什么,求什么,干什么;
设:设未知数注意单位;
找:找等量关系式;
列:用数学语言表达出来;
解:解方程组;
验:检验方程组的解是否符合实际题意;
答:完整写答(包括单位)。
例题1:加工某种产品需经两道工序,第一道工序每人每天可完成 900 件,第二道工序每人每天可完成 1200 件.现有 7 位工人参加这两道工序,应怎样安排人力,才能使每天第一、第二道工序所完成的件数相等?
两个等量关系:第一道工序件数=第二道工序件数
第一道人数+第二道人数=总人数
基本数量关系:工作量=工作效率×人数
解:设第一道工序需要x人,则第二道工序需要y人,
根据题意列方程组得:
解得:
答:第一道工序需要4人,第二道工序需要3人。
课堂练习 (难点巩固) 练习:2台大型收割机和5台小型收割机均工作2小时共收割小麦3.6公顷,3台大型收割机和2台小型收割机均工作5小时共收割小麦8公顷.1台大型收割机和一台小型收割机每小时各收割小麦多少公顷?
解:1台大型收割机和一台小型收割机每小时各收割小麦x公顷,y公顷。
根据题意可得:
解得:
答:1台大型收割机每小时收割小麦0.4公顷,一台小型收割机每小时收割小麦0.2公顷。
板书设计 列方程组解应用题的步骤:
审:有什么,求什么,干什么;
设:设未知数注意单位;
找:找等量关系式;
列:用数学语言表达出来;
解:解方程组;
验:检验方程组的解是否符合实际题意;
答:完整写答(包括单位)。
小结 实际生活中常会遇到解决两个未知量的问题,这两个未知量之间存在数量关系,运用二元一次方程组可以解决这类问题。分析问题中的数量关系→发现等量关系→列出二元一次方程组→解二元一次方程组→得到实际问题的答案,这一典型的建模过程,是数学应用的具体体现。它对于应用其他数学模型(如不等式,函数等)解决实际问题具有很强的示范作用。
本节课是在学生学习了一元一次方程基础上进行的,主下面是关于本节课的几点说明:
1、本节课对教材的内容进行了优化处理,为跳跃较大的知识点作充分的铺垫,密切联系新旧知识,让学生借助已有的知识和方法主动探索新知识,扩大知识结构,发展能力,完善人格,从而使课堂教学真正落实到学生的发展上,体现了以教师为主导、学生为主体,以思想为导向、知识为载体,以方法为中介、训练为主干,以培养学生的思维能力为中心、操作为动力的教学理念。
2、在课堂教学中为学生提供充分的探索空间,注重引导学生分工合作,独立思考,形成主见并进行交流,创设民主、宽松和谐的课堂气氛,让学生畅所欲言,同时进行实验操作,使课堂教学灵活直观,新鲜有趣,从而使课堂教学实现教学思想的先进性、教学目标的整体性、教学过程的有序性、教学方法的灵活性、教学手段的多样性、教学效果的可靠性。
3、注重量化评价与质怀评价相结合,充分利用课堂观察评价、问题讨论评价、学生自我评价等多元化评价,通过几组习题,将学生水平层次记录在案,为学生的学习评价提供充分的科学依据,从而综合检验学生对数学知识、技能的理解,以及学生在学习数学的过程在情感和态度的形成和发展。
单位名称
填写时间
学科 数学 年级/册 七年级(下) 教材版本 人教版
课题名称 第八章 二元一次方程组与实际问题(工作量问题)
教学目标
课标要求:建立方程模型,运用方程解决实际问题,体会方程是刻划现实世界的有效数学模型。
1.会用二元一次方程组解决“探究2”提出的问题.
2.通过思考、讨论、探究事物之间数量关系,建立方程模型,运用方程解决实际问题,体会方程是刻划现实世界的有效数学模型。
3.通过对实际问题的解决,培养学生应用方程的意识,从而提高学生对数学趣味性、现实性、科学性的认识.
重、难点 教学重点 让学生实践与探索,运用二元一次方程解决有关配套与设计问题
教学难点 寻找关键词,列出等量关系.
难点分析 从知识角度分析为什么难 解决实际问题要首先通过设未知数正确找到问题中的两个等量关系,进而建立模型将生活中的实际问题转化为数学问题,通过对数学问题的解答达到解决实际问题的目的。
从学生角度分析为什么难 学生不能正确找出等量关系式,列出方程组
难点教学方法
通过审题、找等量关系,列出方程组。
教学环节
教学过程
导入 上节课我们初步体验了用方程组解决实际问题的全过程,其实生产,生活中还有许多问题也能用方程组解决.
今天,我们再来看研究一个实际生活中的例子。
如何将实际问题转化为数学问题进行解答?
知识讲解 (难点突破) 列方程组解应用题的步骤:
审:有什么,求什么,干什么;
设:设未知数注意单位;
找:找等量关系式;
列:用数学语言表达出来;
解:解方程组;
验:检验方程组的解是否符合实际题意;
答:完整写答(包括单位)。
例题1:加工某种产品需经两道工序,第一道工序每人每天可完成 900 件,第二道工序每人每天可完成 1200 件.现有 7 位工人参加这两道工序,应怎样安排人力,才能使每天第一、第二道工序所完成的件数相等?
两个等量关系:第一道工序件数=第二道工序件数
第一道人数+第二道人数=总人数
基本数量关系:工作量=工作效率×人数
解:设第一道工序需要x人,则第二道工序需要y人,
根据题意列方程组得:
解得:
答:第一道工序需要4人,第二道工序需要3人。
课堂练习 (难点巩固) 练习:2台大型收割机和5台小型收割机均工作2小时共收割小麦3.6公顷,3台大型收割机和2台小型收割机均工作5小时共收割小麦8公顷.1台大型收割机和一台小型收割机每小时各收割小麦多少公顷?
解:1台大型收割机和一台小型收割机每小时各收割小麦x公顷,y公顷。
根据题意可得:
解得:
答:1台大型收割机每小时收割小麦0.4公顷,一台小型收割机每小时收割小麦0.2公顷。
板书设计 列方程组解应用题的步骤:
审:有什么,求什么,干什么;
设:设未知数注意单位;
找:找等量关系式;
列:用数学语言表达出来;
解:解方程组;
验:检验方程组的解是否符合实际题意;
答:完整写答(包括单位)。
小结 实际生活中常会遇到解决两个未知量的问题,这两个未知量之间存在数量关系,运用二元一次方程组可以解决这类问题。分析问题中的数量关系→发现等量关系→列出二元一次方程组→解二元一次方程组→得到实际问题的答案,这一典型的建模过程,是数学应用的具体体现。它对于应用其他数学模型(如不等式,函数等)解决实际问题具有很强的示范作用。
本节课是在学生学习了一元一次方程基础上进行的,主下面是关于本节课的几点说明:
1、本节课对教材的内容进行了优化处理,为跳跃较大的知识点作充分的铺垫,密切联系新旧知识,让学生借助已有的知识和方法主动探索新知识,扩大知识结构,发展能力,完善人格,从而使课堂教学真正落实到学生的发展上,体现了以教师为主导、学生为主体,以思想为导向、知识为载体,以方法为中介、训练为主干,以培养学生的思维能力为中心、操作为动力的教学理念。
2、在课堂教学中为学生提供充分的探索空间,注重引导学生分工合作,独立思考,形成主见并进行交流,创设民主、宽松和谐的课堂气氛,让学生畅所欲言,同时进行实验操作,使课堂教学灵活直观,新鲜有趣,从而使课堂教学实现教学思想的先进性、教学目标的整体性、教学过程的有序性、教学方法的灵活性、教学手段的多样性、教学效果的可靠性。
3、注重量化评价与质怀评价相结合,充分利用课堂观察评价、问题讨论评价、学生自我评价等多元化评价,通过几组习题,将学生水平层次记录在案,为学生的学习评价提供充分的科学依据,从而综合检验学生对数学知识、技能的理解,以及学生在学习数学的过程在情感和态度的形成和发展。
