2020-2021学年人教版八年级数学下册18.1.1 平行四边形的性质课件(共16张)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册18.1.1 平行四边形的性质课件(共16张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 10:24:14 | ||
图片预览




文档简介
(共16张PPT)
18.1
平行四边形
18.1.1平行四边形的性质
1、掌握平行四边形的概念和平行四边形对边、对角相等的性质;
2、会用平行四边形的性质解决简单的平行四边形的问题.
学习目标
情景引入
以上照片中的设施都含有平行四边形样式的结构,回想小学时,我们都学过哪些关于平行四边形的知识?
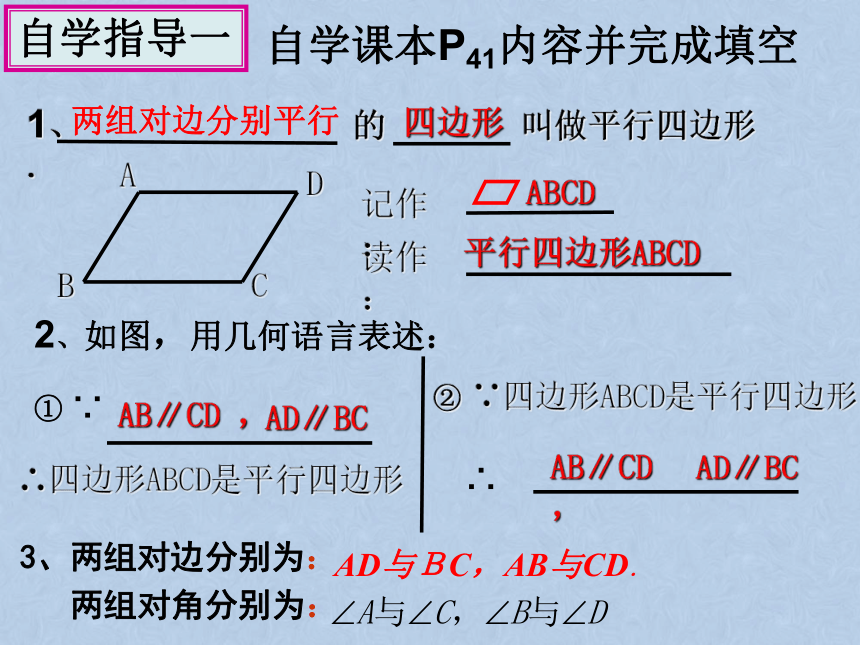
1、
的
叫做平行四边形.
读作:
A
D
B
C
记作:
AB∥CD
,
AD∥BC
①
∵
∴四边形ABCD是平行四边形
②
∵四边形ABCD是平行四边形
AB∥CD
,
AD∥BC
∴
2、如图,用几何语言表述:
自学课本P41内容并完成填空
ABCD
平行四边形ABCD
两组对边分别平行
四边形
自学指导一
3、两组对边分别为:
两组对角分别为:
AD与BC,AB与CD.
自学指导二
1.根据定义画一个平行四边形.
2.观察除了“两组对边平行”外,它的边之间,角之间有什么关系?
3.度量一下,和你的猜想一致吗?
4.试证明你的猜想.
同位合作完成
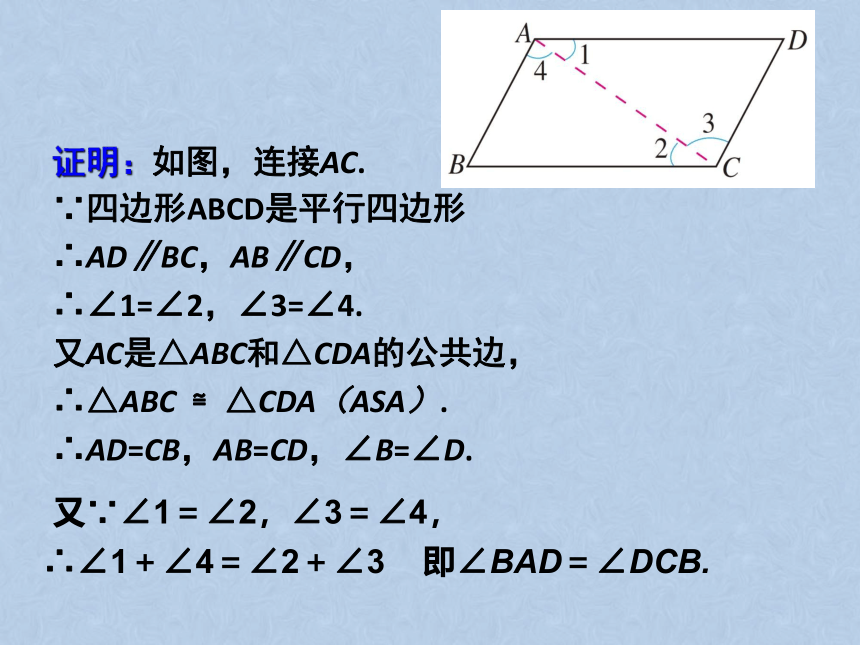
证明:
如图,连接AC.
∵四边形ABCD是平行四边形
∴AD∥BC,AB∥CD,
∴∠1=∠2,∠3=∠4.
又AC是△ABC和△CDA的公共边,
∴△ABC
≌△CDA(ASA).
∴AD=CB,AB=CD,∠B=∠D.
即∠BAD=∠DCB.
又∵∠1=∠2,∠3=∠4,
∴∠1+∠4=∠2+∠3
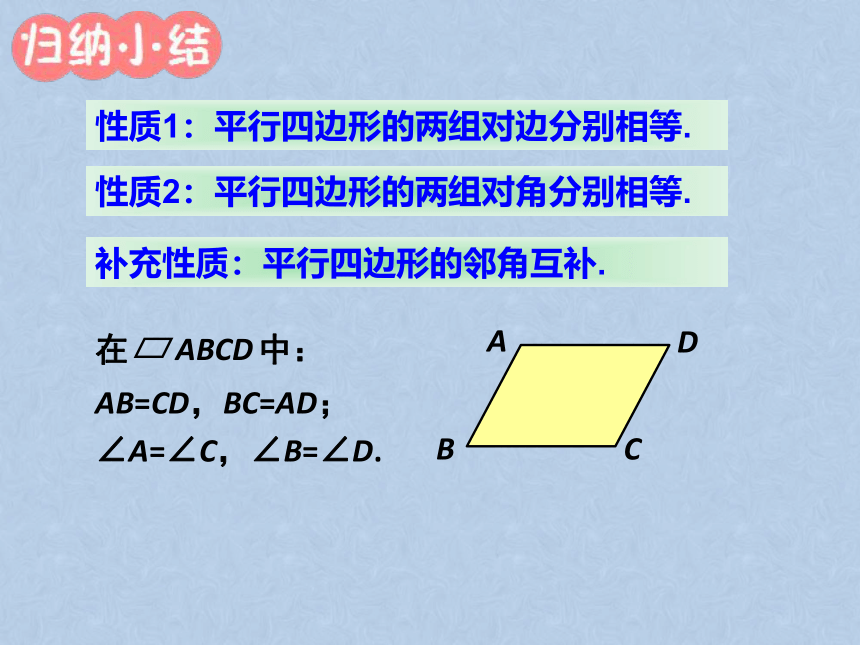
性质1:平行四边形的两组对边分别相等.
性质2:平行四边形的两组对角分别相等.
A
B
C
D
AB=CD,BC=AD;
∠A=∠C,∠B=∠D.
在
中:
ABCD
补充性质:平行四边形的邻角互补.
2、如图,
ABCD中,∠B=50°则∠A=
;
∠C=
;∠D=
;
A
B
C
D
1、如图,
ABCD中,BC=7,AB=5,它的周长为_________.
A
B
C
D
130°
130°
50°
24
学以致用
例1
如图,
ABCD中,DE⊥AB,BF⊥CD,
垂足分别为E,F。
求证:AE=CF
证明:
∵四边形ABCD是平行四边形,
∴
∠A=
∠C,AD=CB.
又∠AED=
∠CFB=90°,
∴
△ADE≌△CBF,
∴AE=CF.
两条平行线之间的距离
合作探究
小结:
如图中DE和BF这样,在两平行线中,一条直线上任意一点到
叫做这两条平行线之间的距离。两条平行线间的距离处处
。
另一条直线的距离
相等
变式(讨论):DE=BF
吗?
DE是点D到点E的距离吗?
DE是点D到直线AB的距离吗?
DE是直线DC到直线AB的距离吗?
例2:如图,a∥b,c∥d,c,d与a,b分别交于A
,B
,C
,D四点,四边形ABCD是
形,
为什么?
小结:两条平行线之间的任何两条平行线段都相等.
平行四边
学以致用
a
b
A
D
C
B
如图,已知a∥b,比较△ABC和△DBC的面积。
1.在□
ABCD中,∠A:∠B=2:3,则∠A=
_____
,∠B=
______,∠C=
______,
∠D=
_______.
2.已知□
ABCD的周长为20cm,且AD-AB=1cm,则
AD=
______,CD=
_____.
5.5cm
4.5cm
3.判断题:(对的在括号内填“√”,错的填“×”)
(1)平行四边形两组对边分别平行且相等.
(
)
(2)平行四边形的四个内角都相等.
(
)
(3)平行四边形的相邻两个内角的和等于180°(
)
(4)如果平行四边形相邻两边长分别是2cm和
3cm,那么周长是10cm.
(
)
(5)在平行四边形ABCD中,如果∠A=42°,
那么∠B=48°.
(
)
(6)在平行四边形ABCD中,如果∠A=35°,
那么∠C=145°.
(
)
√
√
√
×
×
×
当堂巩固
4、有一块形状如图
所示的玻璃,不小心把ED部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
解:
∵四边形ABCD是平行四边形
∴∠D=∠B=60°
AD=BC=80cm
∴DE=AD-AE
=80cm-60cm
=20cm
1.
定义:
四边形
两组对边
平行四边形
分别平行
2.
性质:
对边平行且相等.
对角相等,邻角互补.
两平行线的距离处处相等.
两平行线间的平行线段相等.
平行四边形
总结提升
边:
角:
3.
作业布置
必做题:课本P49,复习巩固1、2题
选做题:课本P50,7题
18.1
平行四边形
18.1.1平行四边形的性质
1、掌握平行四边形的概念和平行四边形对边、对角相等的性质;
2、会用平行四边形的性质解决简单的平行四边形的问题.
学习目标
情景引入
以上照片中的设施都含有平行四边形样式的结构,回想小学时,我们都学过哪些关于平行四边形的知识?
1、
的
叫做平行四边形.
读作:
A
D
B
C
记作:
AB∥CD
,
AD∥BC
①
∵
∴四边形ABCD是平行四边形
②
∵四边形ABCD是平行四边形
AB∥CD
,
AD∥BC
∴
2、如图,用几何语言表述:
自学课本P41内容并完成填空
ABCD
平行四边形ABCD
两组对边分别平行
四边形
自学指导一
3、两组对边分别为:
两组对角分别为:
AD与BC,AB与CD.
自学指导二
1.根据定义画一个平行四边形.
2.观察除了“两组对边平行”外,它的边之间,角之间有什么关系?
3.度量一下,和你的猜想一致吗?
4.试证明你的猜想.
同位合作完成
证明:
如图,连接AC.
∵四边形ABCD是平行四边形
∴AD∥BC,AB∥CD,
∴∠1=∠2,∠3=∠4.
又AC是△ABC和△CDA的公共边,
∴△ABC
≌△CDA(ASA).
∴AD=CB,AB=CD,∠B=∠D.
即∠BAD=∠DCB.
又∵∠1=∠2,∠3=∠4,
∴∠1+∠4=∠2+∠3
性质1:平行四边形的两组对边分别相等.
性质2:平行四边形的两组对角分别相等.
A
B
C
D
AB=CD,BC=AD;
∠A=∠C,∠B=∠D.
在
中:
ABCD
补充性质:平行四边形的邻角互补.
2、如图,
ABCD中,∠B=50°则∠A=
;
∠C=
;∠D=
;
A
B
C
D
1、如图,
ABCD中,BC=7,AB=5,它的周长为_________.
A
B
C
D
130°
130°
50°
24
学以致用
例1
如图,
ABCD中,DE⊥AB,BF⊥CD,
垂足分别为E,F。
求证:AE=CF
证明:
∵四边形ABCD是平行四边形,
∴
∠A=
∠C,AD=CB.
又∠AED=
∠CFB=90°,
∴
△ADE≌△CBF,
∴AE=CF.
两条平行线之间的距离
合作探究
小结:
如图中DE和BF这样,在两平行线中,一条直线上任意一点到
叫做这两条平行线之间的距离。两条平行线间的距离处处
。
另一条直线的距离
相等
变式(讨论):DE=BF
吗?
DE是点D到点E的距离吗?
DE是点D到直线AB的距离吗?
DE是直线DC到直线AB的距离吗?
例2:如图,a∥b,c∥d,c,d与a,b分别交于A
,B
,C
,D四点,四边形ABCD是
形,
为什么?
小结:两条平行线之间的任何两条平行线段都相等.
平行四边
学以致用
a
b
A
D
C
B
如图,已知a∥b,比较△ABC和△DBC的面积。
1.在□
ABCD中,∠A:∠B=2:3,则∠A=
_____
,∠B=
______,∠C=
______,
∠D=
_______.
2.已知□
ABCD的周长为20cm,且AD-AB=1cm,则
AD=
______,CD=
_____.
5.5cm
4.5cm
3.判断题:(对的在括号内填“√”,错的填“×”)
(1)平行四边形两组对边分别平行且相等.
(
)
(2)平行四边形的四个内角都相等.
(
)
(3)平行四边形的相邻两个内角的和等于180°(
)
(4)如果平行四边形相邻两边长分别是2cm和
3cm,那么周长是10cm.
(
)
(5)在平行四边形ABCD中,如果∠A=42°,
那么∠B=48°.
(
)
(6)在平行四边形ABCD中,如果∠A=35°,
那么∠C=145°.
(
)
√
√
√
×
×
×
当堂巩固
4、有一块形状如图
所示的玻璃,不小心把ED部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
解:
∵四边形ABCD是平行四边形
∴∠D=∠B=60°
AD=BC=80cm
∴DE=AD-AE
=80cm-60cm
=20cm
1.
定义:
四边形
两组对边
平行四边形
分别平行
2.
性质:
对边平行且相等.
对角相等,邻角互补.
两平行线的距离处处相等.
两平行线间的平行线段相等.
平行四边形
总结提升
边:
角:
3.
作业布置
必做题:课本P49,复习巩固1、2题
选做题:课本P50,7题
