正方形1
图片预览






文档简介
(共35张PPT)
正方形
操 作
⒈怎样用一张矩形的纸片折出一个正方形?
⒉怎样将一个菱形的木框变成一个正方形的木框?
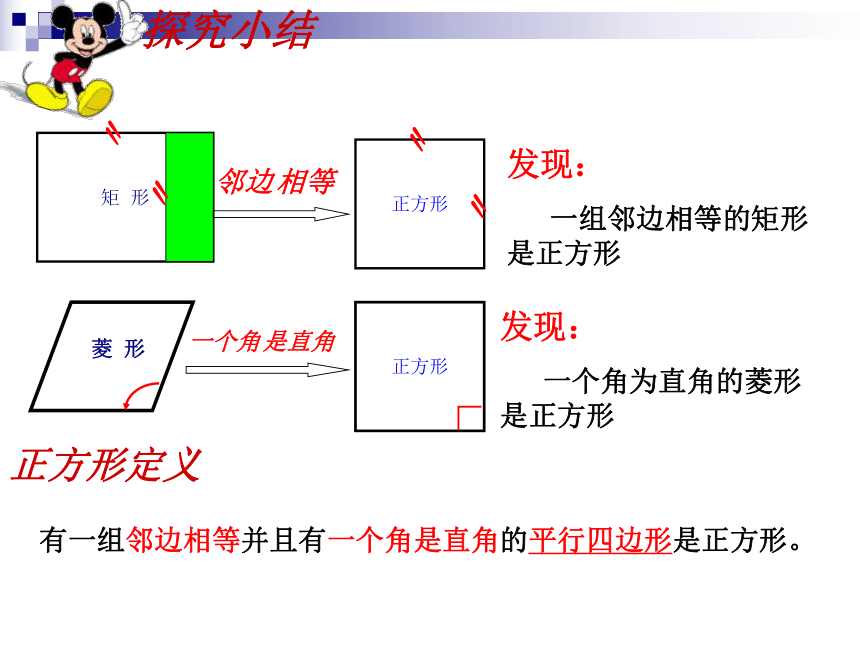
探究小结
矩 形
〃
〃
正方形
邻边
相等
〃
〃
发现:
一组邻边相等的矩形 是正方形
菱 形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形是正方形
正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形。
矩形
菱形
正方形
观察思考:正方形是中心对称图形吗
正方形是轴对称图形吗 有几条对称轴?
讨 论
㈠正方形有什么性质?
边:对边平行,四条边都相等.
角:四个角都相等,都等于90°.
对角线:相等、垂直且互相平分,
每一条对角线平分一组对角.
例
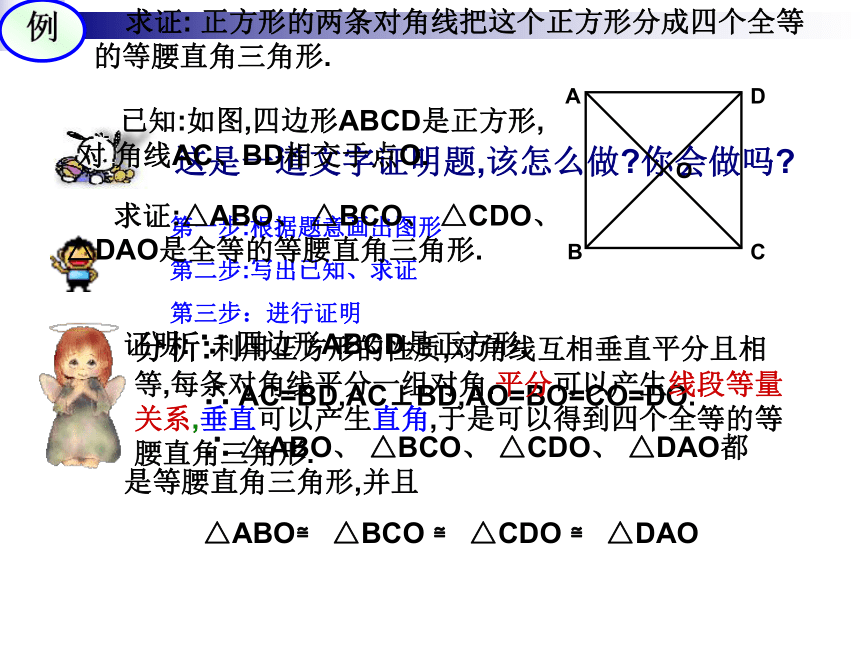
求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
这是一道文字证明题,该怎么做 你会做吗
第一步:根据题意画出图形
第二步:写出已知、求证
第三步:进行证明
A
D
C
B
O
已知:如图,四边形ABCD是正方形,对 角线AC、BD相交于点O.
求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO
分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
A
D
C
B
O
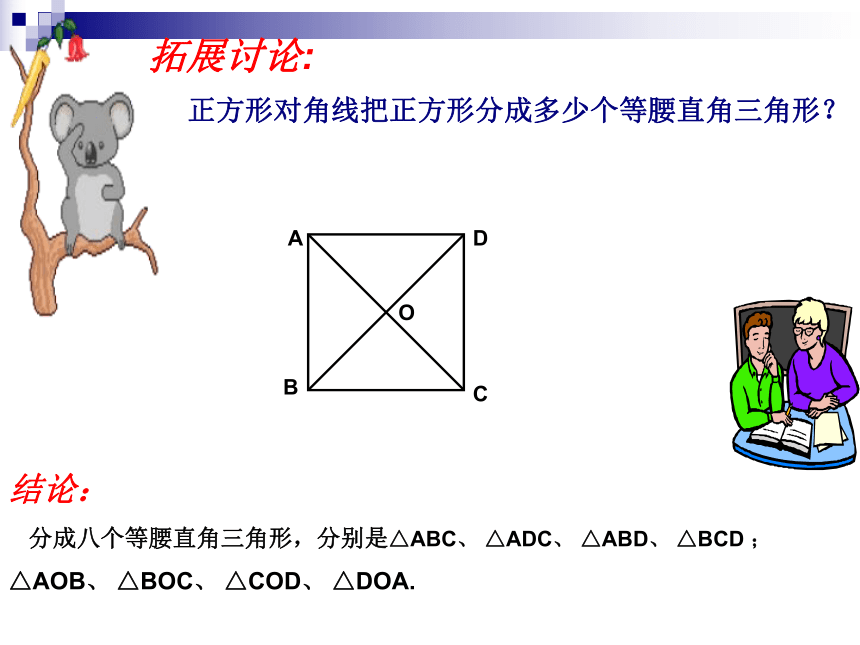
正方形对角线把正方形分成多少个等腰直角三角形?
拓展讨论:
结论:
分成八个等腰直角三角形,分别是△ABC、 △ADC、 △ABD、 △BCD ;
△AOB、 △BOC、 △COD、 △DOA.
讨 论
㈡具备什么条件的平行四边形是正方形?
⒈先说明它是矩形,再说明这个矩形有一组邻边相等.
⒉先说明它是菱形,再说明这个菱形有一个角是直角.
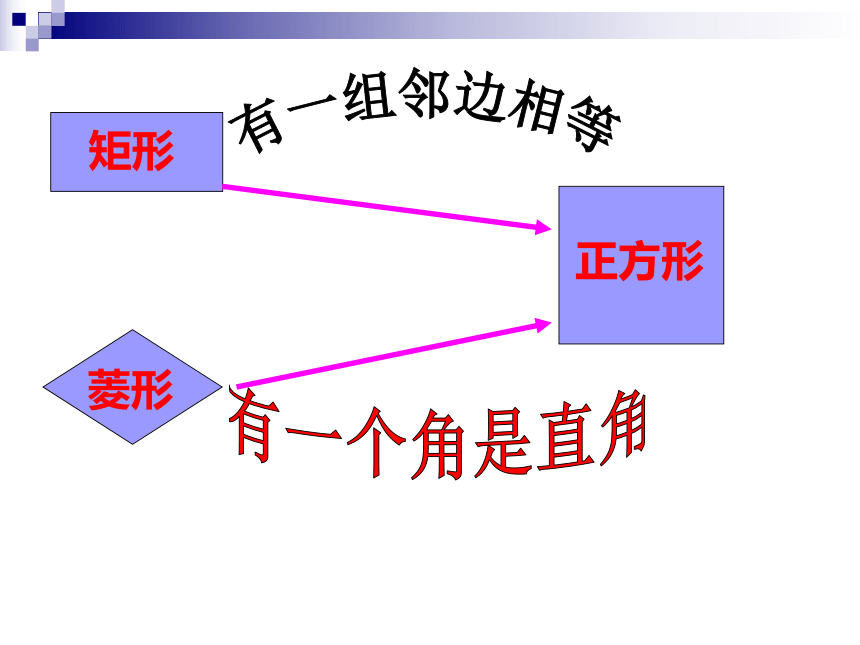
矩形
菱形
正方形
有一组邻边相等
有一个角是直角
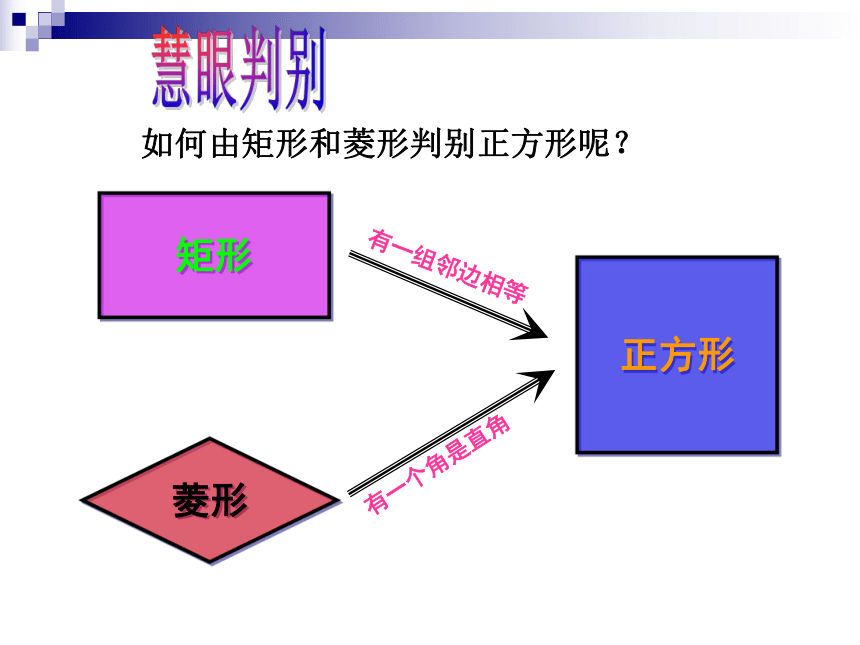
如何由矩形和菱形判别正方形呢?
例1:1、要使一个菱形成为正方形需
增加的条件是
(填上一个条件即可)
2、要使一个矩形成为正方形需添加的条件是
(填上一个条件即可)
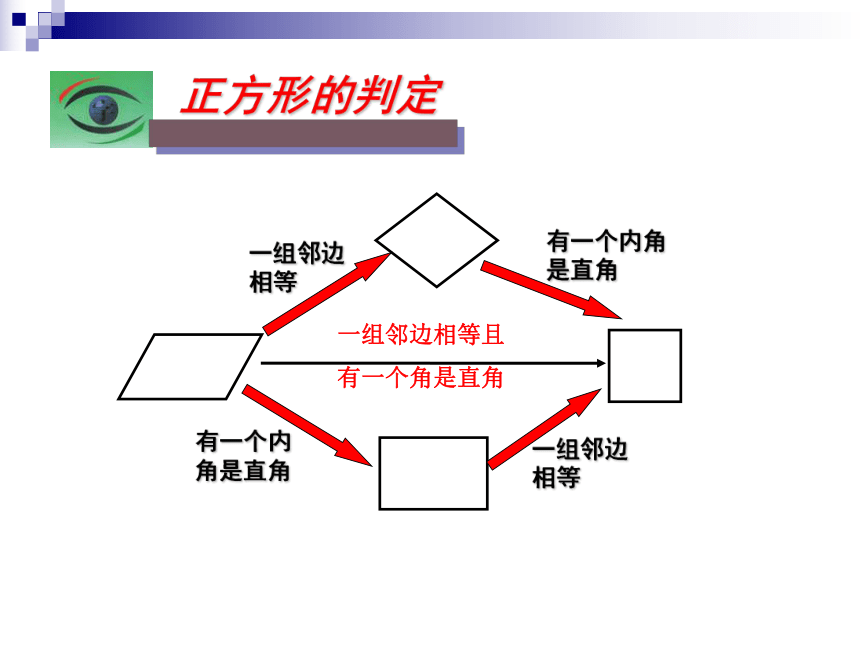
一组邻边相等
有一个内角是直角
一组邻边相等
有一个内角是直角
正方形的判定
一组邻边相等且
有一个角是直角
学而应用之
1.怎样使菱形的衣帽架变成正方形的衣帽架
2.现有一条方巾,想请同学们帮助检验一下方巾是否是正方形的。怎样检验?
已知:正方形ABCD中,点E、F、G 、H分别在AB 、BC 、CD 、DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗 为什么
A
B
C
D
E
F
G
H
1
2
3
证明:∵ 四边形ABCD是正方形
∴ ∠ABC=∠BCD=90°,
AB=AD=DC=BC(正方形的四
条边都相等,四个角都是直角)
又∵ AE=BF=CG=DH
∴AB-AE=AD-DH=DC-CG=BC-BF
即BE=AH=DG=CF
∴ △AEH≌△BFE≌ △CGF ≌ △DHG.
∵ ∠1=∠3.
又 ∠3+∠2=90°
∠1+∠2=90°.
∴ 四边形EFGH是正方形(有一个角是直角的菱形是矩形).
P101练习1、2
练习1 提示:有一组邻边相等的矩形是正方形
A
B
D
C
E
〃
〃
∟
F
正方形
裁
A
D
C
B
E
∟
∟
练习2
提示:寻找直角三角形,运用直角三角形求边长和对角线.
在一块正方形的花坛上,欲修建两条直的小路使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度).你有几种方法?
设计花坛
已知:正方形ABCD中,点E、F、G 、H分别是AB 、BC 、CD 、DA的中点,试判断四边形EFGH是正方形吗 为什么
A
B
C
D
E
F
G
H
小结
1、正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
2、正方形有哪些性质
对边平行,四条边都相等
四个角都是直角
对角线互相垂直平分且相等,
每条对角线平分一组对角
边:
角:
对角线:
平行四边形
矩形
菱形
正
方
形
正方形、菱形、矩形、平行四边形四者之间有什么关系?
补充练习:
1、如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为 平方厘米.
A
B
C
D
2、如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.
(1)求证AE=BF;
(2)若BC= cm,求正方形DEFG的边长.
补充习题:
1、已知正方形ABCD的边长为4,E为BC边上一点,且BE=1,
P为AC上一点,求PE+PB的最小值.
2、在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.
G
F
E
D
A
B
C
如图,四边形ABCD和AEFG都是正方形, 求证:BE = DG
A
B
C
D
E
F
G
例题赏析
⒉在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.
G
F
E
D
A
B
C
数一数图中正方形的个数,你发现了什么?
多
多
多
( )个( )个 ( )个 ( )个
第n个图中正方形有 个
3n-1
长见识
第十九章 四边形
例3.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°
分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____
要证MD=FD,大家只须证得哪两个三角形全等
试一试
看能不能完成证明
△CMD≌△ADF
例3.已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45°
证明:
∵CE⊥AF ∴∠ADC=∠AEM=90° 又∵∠CMD=∠AME ∴∠1=∠2 又∵CD=AD,∠ADF=∠MDC ∴Rt△CDM≌Rt△ADF (AAS) ∴DM=DF
下面的证明请大家完成
练习.如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB
(2) BH⊥AF
证明:
练习:在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
1)试说明:DE=DF
2)只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线,无需证明)
2.在正方形ABCD中,对角线AC、BD相交于点O,点Q是CD上任意一点,DP⊥AQ交BC于点P.
⑴求证:DQ=CP;
⑵OP与OQ有何关系?试证明你的结论.
4.求证:矩形的四个角的平分线所围成的四边形是正方形.
3.如图,以△ABC的边AB、AC向形外作正方形ABDE和ACFG,M是BC的中点.
求证:
⑴CE=BG;
⑵EG=2AM.
H
M
E
D
F
G
B
C
A
教学反思
▲正方形有哪些性质?如何判别一个平行四边形是正方形?
★从角上来谈;
●从边上来谈;
▲从对角线上来谈;
一个角是直角
有一个角是直角且一组邻边相等的平行四边形叫做正方形
正方形
平行四边形
正方形的 两条对角线互相垂直平分且相等,每条对角线平分一组对角
正方形的对边平行且相等
正方形的四个角都是直角
边
对角线
角
正方形的定义
正方形的性质
一组邻边相等
正方形
操 作
⒈怎样用一张矩形的纸片折出一个正方形?
⒉怎样将一个菱形的木框变成一个正方形的木框?
探究小结
矩 形
〃
〃
正方形
邻边
相等
〃
〃
发现:
一组邻边相等的矩形 是正方形
菱 形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形是正方形
正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形。
矩形
菱形
正方形
观察思考:正方形是中心对称图形吗
正方形是轴对称图形吗 有几条对称轴?
讨 论
㈠正方形有什么性质?
边:对边平行,四条边都相等.
角:四个角都相等,都等于90°.
对角线:相等、垂直且互相平分,
每一条对角线平分一组对角.
例
求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
这是一道文字证明题,该怎么做 你会做吗
第一步:根据题意画出图形
第二步:写出已知、求证
第三步:进行证明
A
D
C
B
O
已知:如图,四边形ABCD是正方形,对 角线AC、BD相交于点O.
求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO
分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
A
D
C
B
O
正方形对角线把正方形分成多少个等腰直角三角形?
拓展讨论:
结论:
分成八个等腰直角三角形,分别是△ABC、 △ADC、 △ABD、 △BCD ;
△AOB、 △BOC、 △COD、 △DOA.
讨 论
㈡具备什么条件的平行四边形是正方形?
⒈先说明它是矩形,再说明这个矩形有一组邻边相等.
⒉先说明它是菱形,再说明这个菱形有一个角是直角.
矩形
菱形
正方形
有一组邻边相等
有一个角是直角
如何由矩形和菱形判别正方形呢?
例1:1、要使一个菱形成为正方形需
增加的条件是
(填上一个条件即可)
2、要使一个矩形成为正方形需添加的条件是
(填上一个条件即可)
一组邻边相等
有一个内角是直角
一组邻边相等
有一个内角是直角
正方形的判定
一组邻边相等且
有一个角是直角
学而应用之
1.怎样使菱形的衣帽架变成正方形的衣帽架
2.现有一条方巾,想请同学们帮助检验一下方巾是否是正方形的。怎样检验?
已知:正方形ABCD中,点E、F、G 、H分别在AB 、BC 、CD 、DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗 为什么
A
B
C
D
E
F
G
H
1
2
3
证明:∵ 四边形ABCD是正方形
∴ ∠ABC=∠BCD=90°,
AB=AD=DC=BC(正方形的四
条边都相等,四个角都是直角)
又∵ AE=BF=CG=DH
∴AB-AE=AD-DH=DC-CG=BC-BF
即BE=AH=DG=CF
∴ △AEH≌△BFE≌ △CGF ≌ △DHG.
∵ ∠1=∠3.
又 ∠3+∠2=90°
∠1+∠2=90°.
∴ 四边形EFGH是正方形(有一个角是直角的菱形是矩形).
P101练习1、2
练习1 提示:有一组邻边相等的矩形是正方形
A
B
D
C
E
〃
〃
∟
F
正方形
裁
A
D
C
B
E
∟
∟
练习2
提示:寻找直角三角形,运用直角三角形求边长和对角线.
在一块正方形的花坛上,欲修建两条直的小路使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度).你有几种方法?
设计花坛
已知:正方形ABCD中,点E、F、G 、H分别是AB 、BC 、CD 、DA的中点,试判断四边形EFGH是正方形吗 为什么
A
B
C
D
E
F
G
H
小结
1、正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
2、正方形有哪些性质
对边平行,四条边都相等
四个角都是直角
对角线互相垂直平分且相等,
每条对角线平分一组对角
边:
角:
对角线:
平行四边形
矩形
菱形
正
方
形
正方形、菱形、矩形、平行四边形四者之间有什么关系?
补充练习:
1、如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为 平方厘米.
A
B
C
D
2、如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.
(1)求证AE=BF;
(2)若BC= cm,求正方形DEFG的边长.
补充习题:
1、已知正方形ABCD的边长为4,E为BC边上一点,且BE=1,
P为AC上一点,求PE+PB的最小值.
2、在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.
G
F
E
D
A
B
C
如图,四边形ABCD和AEFG都是正方形, 求证:BE = DG
A
B
C
D
E
F
G
例题赏析
⒉在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.
G
F
E
D
A
B
C
数一数图中正方形的个数,你发现了什么?
多
多
多
( )个( )个 ( )个 ( )个
第n个图中正方形有 个
3n-1
长见识
第十九章 四边形
例3.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°
分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____
要证MD=FD,大家只须证得哪两个三角形全等
试一试
看能不能完成证明
△CMD≌△ADF
例3.已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45°
证明:
∵CE⊥AF ∴∠ADC=∠AEM=90° 又∵∠CMD=∠AME ∴∠1=∠2 又∵CD=AD,∠ADF=∠MDC ∴Rt△CDM≌Rt△ADF (AAS) ∴DM=DF
下面的证明请大家完成
练习.如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB
(2) BH⊥AF
证明:
练习:在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
1)试说明:DE=DF
2)只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线,无需证明)
2.在正方形ABCD中,对角线AC、BD相交于点O,点Q是CD上任意一点,DP⊥AQ交BC于点P.
⑴求证:DQ=CP;
⑵OP与OQ有何关系?试证明你的结论.
4.求证:矩形的四个角的平分线所围成的四边形是正方形.
3.如图,以△ABC的边AB、AC向形外作正方形ABDE和ACFG,M是BC的中点.
求证:
⑴CE=BG;
⑵EG=2AM.
H
M
E
D
F
G
B
C
A
教学反思
▲正方形有哪些性质?如何判别一个平行四边形是正方形?
★从角上来谈;
●从边上来谈;
▲从对角线上来谈;
一个角是直角
有一个角是直角且一组邻边相等的平行四边形叫做正方形
正方形
平行四边形
正方形的 两条对角线互相垂直平分且相等,每条对角线平分一组对角
正方形的对边平行且相等
正方形的四个角都是直角
边
对角线
角
正方形的定义
正方形的性质
一组邻边相等
