20.1.2中位数和众数 2020-2021学年人教版八年级下册数学课件(共40张)
文档属性
| 名称 | 20.1.2中位数和众数 2020-2021学年人教版八年级下册数学课件(共40张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 10:44:01 | ||
图片预览









文档简介
(共40张PPT)
20.2.1数据的集中趋势
(2)中位数与众数
这次数学我考了78分,超过我们班平均分1分,我在班里是中上水平了!!!
哼,什么中上水平,全班30人,27个80分以上的,以及1个2分和1个10分的,倒数第三还差不多!!
小马过河——
河边上的牌子写着“平均深度为1.1m”,
问一匹身高才1.4
m的小马,能涉水过河而不
出危险吗?
?
?
上海某软件科技公司招聘市场销售总监
?
?
要求:大专以上学历,有丰富的市场营销经历,有良好的市场判断能力及社会关系,沟通能力强,对游戏产业有一定的了解。工作地:上海。公司提供业界富有竞争力的薪酬福利待遇,广阔的个人发展空间。
先了解一下该公司的工资情况
问
题
该公司员工的月工资如下:
职员A
职员B
职员E
职员D
职员C
副经理
经理
月工
资/元
员工
1100
1100
1200
1300
6000
1700
4000
500
1100
杂工
职员F
我公司员工收入很高,月平均工资为2000元
我的工资是1200元,在公司算是中等收入.
这个公司员工收入到底怎样呢?
经理
应聘者
职员C
1200元为中等收入是什么意思?
定义:将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;
如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
议一议:(1)你认为那个数据表示该公司员工收入的“平均水平”更合适?
(2)为什么该公司员工收入的平均数比中位数高得多?
职员A
职员B
职员E
职员D
职员C
副经理
经理
月工
资/元
员工
1100
1100
1200
1300
6000
1700
4000
500
1100
杂工
职员F
应聘者小范
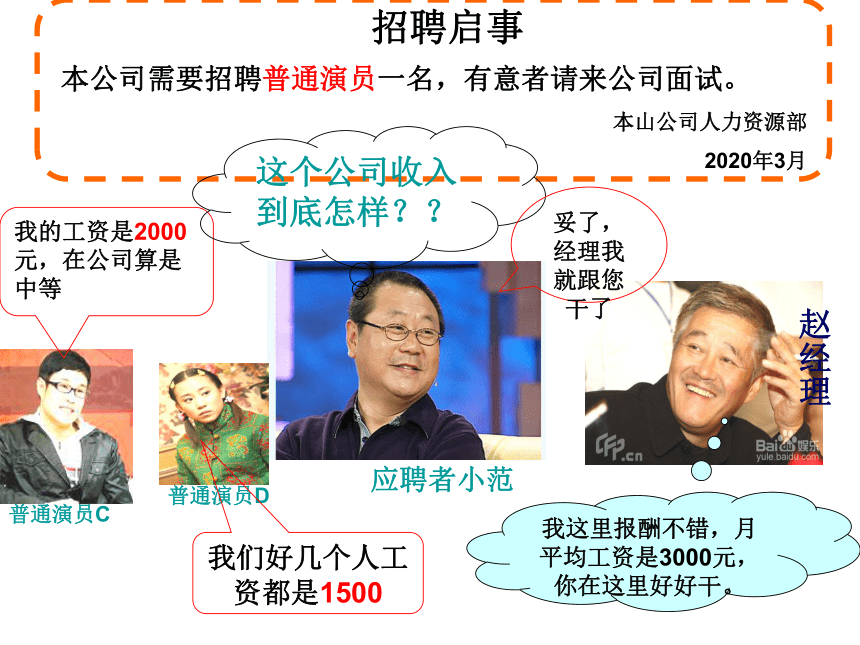
招聘启事
本公司需要招聘普通演员一名,有意者请来公司面试。
本山公司人力资源部
2010年4月
招聘启事
本公司需要招聘普通演员一名,有意者请来公司面试。
本山公司人力资源部
2020年3月
我这里报酬不错,月平均工资是3000元,你在这里好好干。
普通演员C
我的工资是2000元,在公司算是中等
普通演员D
赵经理
这个公司收入到底怎样??
妥了,经理我就跟您干了
我们好几个人工资都是1500
第二天
小范上班了。。。。。。
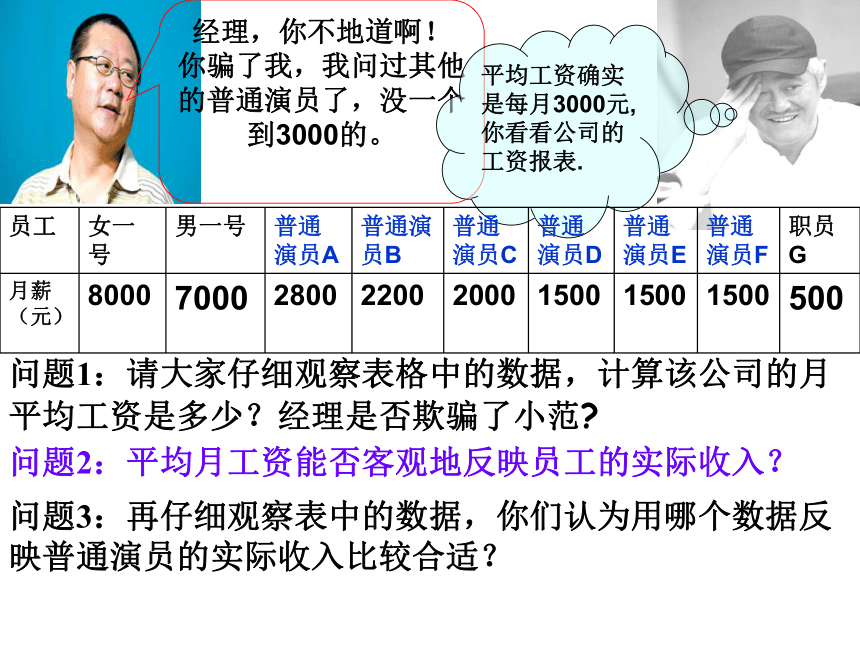
经理,你不地道啊!
你骗了我,我问过其他的普通演员了,没一个到3000的。
平均工资确实是每月3000元,你看看公司的工资报表.
员工
女一号
男一号
普通演员A
普通演员B
普通演员C
普通
演员D
普通演员E
普通演员F
职员G
月薪
(元)
8000
7000
2800
2200
2000
1500
1500
1500
500
问题1:请大家仔细观察表格中的数据,计算该公司的月平均工资是多少?经理是否欺骗了小范?
问题2:平均月工资能否客观地反映员工的实际收入?
问题3:再仔细观察表中的数据,你们认为用哪个数据反映普通演员的实际收入比较合适?
例
题
180,
124,
154,146,
145,
158,
175,
165,
148
(1)样本数据(12名选手的成绩)的中位数是多少?
(2)一名选手的成绩是142分,他的成绩如何?
在一次男子马拉松长跑比赛中,抽得12名选手的成绩如下(单位:分):
136,
140,
129,
解:(1)先将样本数据按照由小到大的顺序排列:124,129,136,140,145,146,148,154,158,165,175,180
则这组数据的中位数为处于中间的两个数146,148的平均数,即:
(146+148)÷2=147
因此样本数据的中位数是147。
(2)根据(1)中得到的样本数据的结论,可以估计,在这次马拉松比赛中,大约有一半选手的成绩快于147分,有一半选手的成绩慢于147分。这名选手的成绩是142分,快于中位数147分,可以推测他的成绩比一半以上的选手的成绩好。
求中位数的一般步骤:
1、将这一组数据从大到小(或从小大大)排列;
2、若该数据含有奇数个数,位于中间位置的数是中位数;
若该数据含有偶数个数,位于中间两个数的平均数就是中位数。
议一议
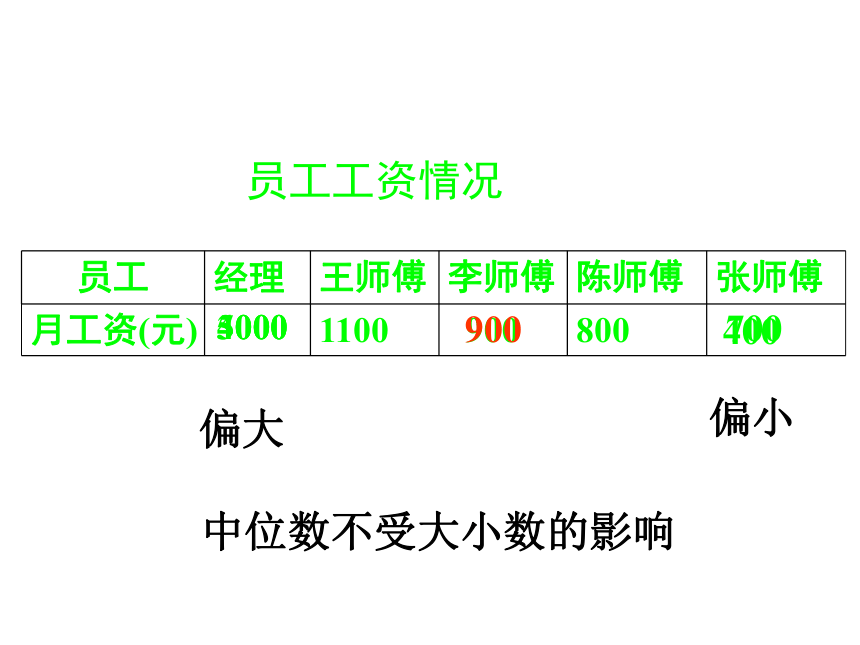
员工工资情况
员工
经理
王师傅
李师傅
陈师傅
张师傅
月工资(元)
1100
900
800
3000
4000
900
5000
700
400
偏大
偏小
中位数不受大小数的影响
中位数:将一组数据按照由小到大(或由大到小)的顺序排列如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数。如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数。
1.数据
3
,1,2
,4
,5
的中位数是(
)
2.数据3,6,1,5,2,4的中位数是(
)
3.数据3,3,3,3,3,3的中位数是(
)
中位数
中
中位数是一个位置代表值。如果已知一组数据的中位数,那么可以知道,小于等于或大于等于这个中位数的数据各占一半。
3
1
5
2
4
1
2
4
3
6
5
众数:一组数据中出现次数最多的数据就是这组数据的众数
1.数据2,1,5,2,1,2的众数是(
)
2.数据3,6,2,5,2,3的众数是(
)
3.数据3,3,3,3,3,3的众数是(
)
4.数据1,2,3,4,5,6的众数是(
)
众数
当一组数据中多个数据出现的次数都是最多时,这几个数据都是这组数据的众数。
2、2、3、3、4、4、5、5、?
6、6这组数众数是多少?
众数:2、3、4、5
2、3、4、5、?6、7、9、12这组数众数是多少?
众数:可以没有
可以不止一个
来源于生活,应用于生活
邓晓彤的成绩为:
16.6米,
他的成绩如何?
4月28日我校将举办第四届中小学田径运动会,我班邓晓彤同学报名参加男子实心球项目的比赛,下表是随机抽取的上一届8名选手的成绩
(单位:米)
A
B
C
D
E
F
G
H
9.6
25.6
15.6
18.8
16.8
17.6
15.0
12.4
车速统计表
车序号
1
2
3
4
5
6
车速(千米/时)
66
57
71
54
69
58
将6辆车的速度按从小到大的顺序排列,得到
54
57
58
66
69
71
正中间的数值不是一个而是两个,所以取这两个数的平均数作为中位数:
(58+66)
÷
2=62
(千米/时)
这6辆车速的平均数、中位数和众数分别是多少?
解:
平均数:(66+57+71+54+69+58)÷6=62.5
没有哪个车速出现的次数比别的多,所以这6辆车的速度没有众数
练一练
平均数、中位数的联系与区别
联系:它们从不同角度描述了一组数据的集中趋势。
区别:计算平均数时,所有数据都参加运算,它能充分利用数据所提供的信息,但容易受极端值的影响。它应用最为广泛。
中位数的优点是计算简单,只与其在数据中的位置有关。但不能充分利用所有的数据信息。
想一想
试一试
1、在一次数学竞赛中,5名学生的成绩从低到高排列依
次是
55,57,61,62,98,那么他们的中位数是多少?
2、10名工人某天生产同一零件,生产的件数是
15,17,14,10,15,19,17,16,14,12,求这一天10名工人生产的零件的中位数。
15
3、某班一组12人的英语成绩如下:
84,73,89,78,83,86,89,84,100,100,78,100.则这12个数的平均数是_____,中位数是______.
4、一组数据按从小到大顺序排列为:13、14、19、x、23、27、28、31,其中位数是22,则x为_______.
87
85
21
平均数:
中位数:
众
数:
数据代表(集中趋势)
归纳小结,知识提升
能充分利用所有数据,
但容易受极端值的影响
计算简单,只与其在数据中的位置有关,
但不能充分利用所有数据
计算简单,只与其在数据中的重复次数有关,
但不能充分利用所有数据
实例
(应用最广)
平均数
中位数
众
数
反映总体平均水平
反映中等水平
反映多数集中水平
平均数
中位数
众
数
A.
多数水平
B.
平均水平
C.
中等水平
平均数反映一组数据的(
)
中位数反映一组数据的(
)
众
数反映一组数据的(
)
B
C
A
选一选
(1)中位数、众数的定义。(注意:确定中位数时要分数据个数是奇数个还是偶数个;众数的个数可能不止一个。)
(3)中位数、众数的作用:
中位数是用来描述数据的集中趋势的,它是一个位置代表值。如果知道一组数据的中位数,那么可以知道,小于或大于这个中位数的数据约各占一半。
众数也常作为一组数据的代表,用来描述数据的集中趋势。当一组数据有较多的重复数据时,众数往往是人们所关心的一个量。
(2)平均数、中位数、众数的优缺点:
平均数:
中位数:
众
数:
能充分利用所有数据,
但容易受极端值的影响
计算简单,只与其在数据中的位置有关,
但不能充分利用所有数据
计算简单,只与其在数据中的重复次数有关,
但不能充分利用所有数据
反映整体情况,但容易受偏大数或偏的影响,有时不能真实地反映一数据的整体情况。
用平均数进行统计的特点:
平均数的大小与一组数据里的每个
数据都有关系,任何一个数据的变动
都会引起平均数的变化.
一组数据中只有一个平均数.
中位数反映一组数据的一般情况,不受偏大或偏小数的影响。
中位数的特点:
众数的特点:
能够反映一组数据的集中情
况。众数与大小无关,与位置无关。
接16
平均数:?一组数据的平均值。(总数量÷总份数)??????总体水平?
???
中位数:?在有序排列的一组数据中最居中的那个数据???一般水平?
???
众??数?:?一组数据中出现次数最多的那个数据。???????集中趋势
真知辨是非
1.一组数据的平均数一定只有一个(
)
2.一组数据的中位数一定只有一个(
)
3.一组数据的中位数一定是这组数据中的
某个数
(
)
4.一组数据的众数一定只有一个
(
)
5.一组数据的平均数、中位数、众数可以
是同一个数
(
)
尺码/厘米
22
22.5
23
23.5
24
24.5
25
销售量/双
1
2
5
11
7
3
1
豪绅鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如下表所示:
你能根据上面的数据为这家鞋店提供进货建议吗?
3、某公司有15名员工,他们所在部门及相应每人所创年利润如下表所示:(单位:万元)
(1)该公司每人所创的年利润的平均数和中位数各多少?
(2)你认为使用平均数和中位数中哪一个描述该公司所创年利润的一般水平比较合理?
部门
A
B
C
D
E
F
G
人数
1
1
2
4
2
2
3
利润
20
5
2.5
2.1
1.5
1.5
1.2
3.2
2.1
中位数
做一做
在青年歌手冠亚军决赛中,11位评委给两位歌手的打分如下。
一
?9.8
?9.7
?9.7
9.6
?9.6
9.6
9.6
9.5
?9.4
9.4
?9.1
二
?10
?9.7
9.6
?
9.6
?9.6
?
9.6
9.5
?
9.5
9.4
?9.4
?9.2
(1)你认为哪位歌手的最后得分高,为什么?
(2)按照“去掉一个最高分,去掉一个最低分,再计算平均分”的方法来计算,平均分是多少?你认为这样做是否有道理?为什么?
生活中的数学
你去商场买过服装吗
?你知道休闲类服装型号的“均码”是什么意思吗?
尺寸:均码
价格:30元
尺寸:均码
价格:25元
均码一般是根据人的平均身高、胸围等数据确定的统一商品型号,与多数人的型号接近。所以,均码里蕴涵着平均数和众数的原理。
众数能够反映一组数据的集中情况.
众数意义:
中位数的特点:
众数的特点:
反映整体情况,但容易受偏大
数或偏小数的影响。
平均数的特点:
中位数反映一组数据的一般情况,不受偏大或偏小数的影响。
一组数据中出现的次数最多的数,
是这组数据的众数。
求平均的方法:总量÷总分数=平均数
找中位数的方法:先按一定的顺序排列,
再找中间数,如数的个数是偶个数的,用中间
两个数的和除以2。
找众数的方法:找出一组数中相同的一个或
者几个数,如果没有相同数,就没有众数。
例:一家鞋店在一段时间内销售了某种女鞋30双,各种尺码的销售量如下表:
尺码(厘米)
22
22.5
23
23.5
24
24.5
25
销售量(双)
1
2
5
11
7
3
1
问:如果你是这家鞋店的经理,对下一步的进货你有何计划?
作为经理,这是我们最关心的一个量哦
注意:平均数、中位数和众数都有单位,它们的单位是与数据的单位相同的。
1、一家童装店最近销售了某种童装30件,销售量如下表所示:
分别求出这个童装店销售童装的众数、中位数和平均数,它们各代表什么?如果你是店主,你最关心的是什么数?
2、数据11,
8,
2,
7,
9,
2,
7,
3,
2,
0,
5的众数是
。
3、数据15,
20,
20,
22,30,30的众数是
。
4、数据8,
8,
x,
6的众数与平均数相同,那么它们的中位数是
。
5、(中考链接)5个正整数从小到大排列,若这组数据的中位数是3,众数是
7且唯一,则这5个正整数的和是(
)
A.20
B.21
C.22
D.23
2
20、30
10
A
尺码(厘米)
100
105
110
115
120
125
130
销售量(件)
1
2
5
11
7
3
1
1.有人对展览馆七天中每天进馆参观的人数做了记录,情况如下:
180,176,176,173,176,181,182
求这组数据的中位数和众数。
众数:
176
中位数:
176
[本课作业]
8同学在某次考试中,最高
得分是95分,最低得分是65分,
他们8人的平均成绩是87.5分,
去掉最低分和最高分后,其余6
位同学的平均成绩是多少?
这一节课我们主要研究了什么问题?
1、中位数——数据的代表;
(1)如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数。
(2)如果数据的个数是偶数,则处于中间两个数的平均数就是这组数据的中位数。
2、已知一组数据的中位数,那么可以知道小于或大于这个数的数据各占一半。
3、平均数、中位数的联系与区别“计算平均数时,所有数据都参加运算,它能充分利用数据所提供的信息,但容易受极端值的影响。它应用最为广泛。
中位数的优点是计算简单,只与其在数据中的位置有关。但不能充分利用所有的数据信息。”
小
结
小
结
1计算平均数的时候,所有的数据都参加运算,它能充分利用数据所提供的信息,在现实生活中较为常用;但它容易受到极端值的影响。
2中位数的优点计算简单,受极端值的影响较小,但不能充分利用所有数据的信息。
3一组数据中某些数据多次重复出现时,众数往往是人们尤为关心的一个量,一组数据可以有不止一个众数,也可以没有众数。但各个数据的重复次数大致相等时,众数往往没有特别意义。
20.2.1数据的集中趋势
(2)中位数与众数
这次数学我考了78分,超过我们班平均分1分,我在班里是中上水平了!!!
哼,什么中上水平,全班30人,27个80分以上的,以及1个2分和1个10分的,倒数第三还差不多!!
小马过河——
河边上的牌子写着“平均深度为1.1m”,
问一匹身高才1.4
m的小马,能涉水过河而不
出危险吗?
?
?
上海某软件科技公司招聘市场销售总监
?
?
要求:大专以上学历,有丰富的市场营销经历,有良好的市场判断能力及社会关系,沟通能力强,对游戏产业有一定的了解。工作地:上海。公司提供业界富有竞争力的薪酬福利待遇,广阔的个人发展空间。
先了解一下该公司的工资情况
问
题
该公司员工的月工资如下:
职员A
职员B
职员E
职员D
职员C
副经理
经理
月工
资/元
员工
1100
1100
1200
1300
6000
1700
4000
500
1100
杂工
职员F
我公司员工收入很高,月平均工资为2000元
我的工资是1200元,在公司算是中等收入.
这个公司员工收入到底怎样呢?
经理
应聘者
职员C
1200元为中等收入是什么意思?
定义:将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;
如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
议一议:(1)你认为那个数据表示该公司员工收入的“平均水平”更合适?
(2)为什么该公司员工收入的平均数比中位数高得多?
职员A
职员B
职员E
职员D
职员C
副经理
经理
月工
资/元
员工
1100
1100
1200
1300
6000
1700
4000
500
1100
杂工
职员F
应聘者小范
招聘启事
本公司需要招聘普通演员一名,有意者请来公司面试。
本山公司人力资源部
2010年4月
招聘启事
本公司需要招聘普通演员一名,有意者请来公司面试。
本山公司人力资源部
2020年3月
我这里报酬不错,月平均工资是3000元,你在这里好好干。
普通演员C
我的工资是2000元,在公司算是中等
普通演员D
赵经理
这个公司收入到底怎样??
妥了,经理我就跟您干了
我们好几个人工资都是1500
第二天
小范上班了。。。。。。
经理,你不地道啊!
你骗了我,我问过其他的普通演员了,没一个到3000的。
平均工资确实是每月3000元,你看看公司的工资报表.
员工
女一号
男一号
普通演员A
普通演员B
普通演员C
普通
演员D
普通演员E
普通演员F
职员G
月薪
(元)
8000
7000
2800
2200
2000
1500
1500
1500
500
问题1:请大家仔细观察表格中的数据,计算该公司的月平均工资是多少?经理是否欺骗了小范?
问题2:平均月工资能否客观地反映员工的实际收入?
问题3:再仔细观察表中的数据,你们认为用哪个数据反映普通演员的实际收入比较合适?
例
题
180,
124,
154,146,
145,
158,
175,
165,
148
(1)样本数据(12名选手的成绩)的中位数是多少?
(2)一名选手的成绩是142分,他的成绩如何?
在一次男子马拉松长跑比赛中,抽得12名选手的成绩如下(单位:分):
136,
140,
129,
解:(1)先将样本数据按照由小到大的顺序排列:124,129,136,140,145,146,148,154,158,165,175,180
则这组数据的中位数为处于中间的两个数146,148的平均数,即:
(146+148)÷2=147
因此样本数据的中位数是147。
(2)根据(1)中得到的样本数据的结论,可以估计,在这次马拉松比赛中,大约有一半选手的成绩快于147分,有一半选手的成绩慢于147分。这名选手的成绩是142分,快于中位数147分,可以推测他的成绩比一半以上的选手的成绩好。
求中位数的一般步骤:
1、将这一组数据从大到小(或从小大大)排列;
2、若该数据含有奇数个数,位于中间位置的数是中位数;
若该数据含有偶数个数,位于中间两个数的平均数就是中位数。
议一议
员工工资情况
员工
经理
王师傅
李师傅
陈师傅
张师傅
月工资(元)
1100
900
800
3000
4000
900
5000
700
400
偏大
偏小
中位数不受大小数的影响
中位数:将一组数据按照由小到大(或由大到小)的顺序排列如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数。如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数。
1.数据
3
,1,2
,4
,5
的中位数是(
)
2.数据3,6,1,5,2,4的中位数是(
)
3.数据3,3,3,3,3,3的中位数是(
)
中位数
中
中位数是一个位置代表值。如果已知一组数据的中位数,那么可以知道,小于等于或大于等于这个中位数的数据各占一半。
3
1
5
2
4
1
2
4
3
6
5
众数:一组数据中出现次数最多的数据就是这组数据的众数
1.数据2,1,5,2,1,2的众数是(
)
2.数据3,6,2,5,2,3的众数是(
)
3.数据3,3,3,3,3,3的众数是(
)
4.数据1,2,3,4,5,6的众数是(
)
众数
当一组数据中多个数据出现的次数都是最多时,这几个数据都是这组数据的众数。
2、2、3、3、4、4、5、5、?
6、6这组数众数是多少?
众数:2、3、4、5
2、3、4、5、?6、7、9、12这组数众数是多少?
众数:可以没有
可以不止一个
来源于生活,应用于生活
邓晓彤的成绩为:
16.6米,
他的成绩如何?
4月28日我校将举办第四届中小学田径运动会,我班邓晓彤同学报名参加男子实心球项目的比赛,下表是随机抽取的上一届8名选手的成绩
(单位:米)
A
B
C
D
E
F
G
H
9.6
25.6
15.6
18.8
16.8
17.6
15.0
12.4
车速统计表
车序号
1
2
3
4
5
6
车速(千米/时)
66
57
71
54
69
58
将6辆车的速度按从小到大的顺序排列,得到
54
57
58
66
69
71
正中间的数值不是一个而是两个,所以取这两个数的平均数作为中位数:
(58+66)
÷
2=62
(千米/时)
这6辆车速的平均数、中位数和众数分别是多少?
解:
平均数:(66+57+71+54+69+58)÷6=62.5
没有哪个车速出现的次数比别的多,所以这6辆车的速度没有众数
练一练
平均数、中位数的联系与区别
联系:它们从不同角度描述了一组数据的集中趋势。
区别:计算平均数时,所有数据都参加运算,它能充分利用数据所提供的信息,但容易受极端值的影响。它应用最为广泛。
中位数的优点是计算简单,只与其在数据中的位置有关。但不能充分利用所有的数据信息。
想一想
试一试
1、在一次数学竞赛中,5名学生的成绩从低到高排列依
次是
55,57,61,62,98,那么他们的中位数是多少?
2、10名工人某天生产同一零件,生产的件数是
15,17,14,10,15,19,17,16,14,12,求这一天10名工人生产的零件的中位数。
15
3、某班一组12人的英语成绩如下:
84,73,89,78,83,86,89,84,100,100,78,100.则这12个数的平均数是_____,中位数是______.
4、一组数据按从小到大顺序排列为:13、14、19、x、23、27、28、31,其中位数是22,则x为_______.
87
85
21
平均数:
中位数:
众
数:
数据代表(集中趋势)
归纳小结,知识提升
能充分利用所有数据,
但容易受极端值的影响
计算简单,只与其在数据中的位置有关,
但不能充分利用所有数据
计算简单,只与其在数据中的重复次数有关,
但不能充分利用所有数据
实例
(应用最广)
平均数
中位数
众
数
反映总体平均水平
反映中等水平
反映多数集中水平
平均数
中位数
众
数
A.
多数水平
B.
平均水平
C.
中等水平
平均数反映一组数据的(
)
中位数反映一组数据的(
)
众
数反映一组数据的(
)
B
C
A
选一选
(1)中位数、众数的定义。(注意:确定中位数时要分数据个数是奇数个还是偶数个;众数的个数可能不止一个。)
(3)中位数、众数的作用:
中位数是用来描述数据的集中趋势的,它是一个位置代表值。如果知道一组数据的中位数,那么可以知道,小于或大于这个中位数的数据约各占一半。
众数也常作为一组数据的代表,用来描述数据的集中趋势。当一组数据有较多的重复数据时,众数往往是人们所关心的一个量。
(2)平均数、中位数、众数的优缺点:
平均数:
中位数:
众
数:
能充分利用所有数据,
但容易受极端值的影响
计算简单,只与其在数据中的位置有关,
但不能充分利用所有数据
计算简单,只与其在数据中的重复次数有关,
但不能充分利用所有数据
反映整体情况,但容易受偏大数或偏的影响,有时不能真实地反映一数据的整体情况。
用平均数进行统计的特点:
平均数的大小与一组数据里的每个
数据都有关系,任何一个数据的变动
都会引起平均数的变化.
一组数据中只有一个平均数.
中位数反映一组数据的一般情况,不受偏大或偏小数的影响。
中位数的特点:
众数的特点:
能够反映一组数据的集中情
况。众数与大小无关,与位置无关。
接16
平均数:?一组数据的平均值。(总数量÷总份数)??????总体水平?
???
中位数:?在有序排列的一组数据中最居中的那个数据???一般水平?
???
众??数?:?一组数据中出现次数最多的那个数据。???????集中趋势
真知辨是非
1.一组数据的平均数一定只有一个(
)
2.一组数据的中位数一定只有一个(
)
3.一组数据的中位数一定是这组数据中的
某个数
(
)
4.一组数据的众数一定只有一个
(
)
5.一组数据的平均数、中位数、众数可以
是同一个数
(
)
尺码/厘米
22
22.5
23
23.5
24
24.5
25
销售量/双
1
2
5
11
7
3
1
豪绅鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如下表所示:
你能根据上面的数据为这家鞋店提供进货建议吗?
3、某公司有15名员工,他们所在部门及相应每人所创年利润如下表所示:(单位:万元)
(1)该公司每人所创的年利润的平均数和中位数各多少?
(2)你认为使用平均数和中位数中哪一个描述该公司所创年利润的一般水平比较合理?
部门
A
B
C
D
E
F
G
人数
1
1
2
4
2
2
3
利润
20
5
2.5
2.1
1.5
1.5
1.2
3.2
2.1
中位数
做一做
在青年歌手冠亚军决赛中,11位评委给两位歌手的打分如下。
一
?9.8
?9.7
?9.7
9.6
?9.6
9.6
9.6
9.5
?9.4
9.4
?9.1
二
?10
?9.7
9.6
?
9.6
?9.6
?
9.6
9.5
?
9.5
9.4
?9.4
?9.2
(1)你认为哪位歌手的最后得分高,为什么?
(2)按照“去掉一个最高分,去掉一个最低分,再计算平均分”的方法来计算,平均分是多少?你认为这样做是否有道理?为什么?
生活中的数学
你去商场买过服装吗
?你知道休闲类服装型号的“均码”是什么意思吗?
尺寸:均码
价格:30元
尺寸:均码
价格:25元
均码一般是根据人的平均身高、胸围等数据确定的统一商品型号,与多数人的型号接近。所以,均码里蕴涵着平均数和众数的原理。
众数能够反映一组数据的集中情况.
众数意义:
中位数的特点:
众数的特点:
反映整体情况,但容易受偏大
数或偏小数的影响。
平均数的特点:
中位数反映一组数据的一般情况,不受偏大或偏小数的影响。
一组数据中出现的次数最多的数,
是这组数据的众数。
求平均的方法:总量÷总分数=平均数
找中位数的方法:先按一定的顺序排列,
再找中间数,如数的个数是偶个数的,用中间
两个数的和除以2。
找众数的方法:找出一组数中相同的一个或
者几个数,如果没有相同数,就没有众数。
例:一家鞋店在一段时间内销售了某种女鞋30双,各种尺码的销售量如下表:
尺码(厘米)
22
22.5
23
23.5
24
24.5
25
销售量(双)
1
2
5
11
7
3
1
问:如果你是这家鞋店的经理,对下一步的进货你有何计划?
作为经理,这是我们最关心的一个量哦
注意:平均数、中位数和众数都有单位,它们的单位是与数据的单位相同的。
1、一家童装店最近销售了某种童装30件,销售量如下表所示:
分别求出这个童装店销售童装的众数、中位数和平均数,它们各代表什么?如果你是店主,你最关心的是什么数?
2、数据11,
8,
2,
7,
9,
2,
7,
3,
2,
0,
5的众数是
。
3、数据15,
20,
20,
22,30,30的众数是
。
4、数据8,
8,
x,
6的众数与平均数相同,那么它们的中位数是
。
5、(中考链接)5个正整数从小到大排列,若这组数据的中位数是3,众数是
7且唯一,则这5个正整数的和是(
)
A.20
B.21
C.22
D.23
2
20、30
10
A
尺码(厘米)
100
105
110
115
120
125
130
销售量(件)
1
2
5
11
7
3
1
1.有人对展览馆七天中每天进馆参观的人数做了记录,情况如下:
180,176,176,173,176,181,182
求这组数据的中位数和众数。
众数:
176
中位数:
176
[本课作业]
8同学在某次考试中,最高
得分是95分,最低得分是65分,
他们8人的平均成绩是87.5分,
去掉最低分和最高分后,其余6
位同学的平均成绩是多少?
这一节课我们主要研究了什么问题?
1、中位数——数据的代表;
(1)如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数。
(2)如果数据的个数是偶数,则处于中间两个数的平均数就是这组数据的中位数。
2、已知一组数据的中位数,那么可以知道小于或大于这个数的数据各占一半。
3、平均数、中位数的联系与区别“计算平均数时,所有数据都参加运算,它能充分利用数据所提供的信息,但容易受极端值的影响。它应用最为广泛。
中位数的优点是计算简单,只与其在数据中的位置有关。但不能充分利用所有的数据信息。”
小
结
小
结
1计算平均数的时候,所有的数据都参加运算,它能充分利用数据所提供的信息,在现实生活中较为常用;但它容易受到极端值的影响。
2中位数的优点计算简单,受极端值的影响较小,但不能充分利用所有数据的信息。
3一组数据中某些数据多次重复出现时,众数往往是人们尤为关心的一个量,一组数据可以有不止一个众数,也可以没有众数。但各个数据的重复次数大致相等时,众数往往没有特别意义。
