§12.3.1等腰三角形的性质
文档属性
| 名称 | §12.3.1等腰三角形的性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 1009.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-26 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
12.3.1 等腰三角形
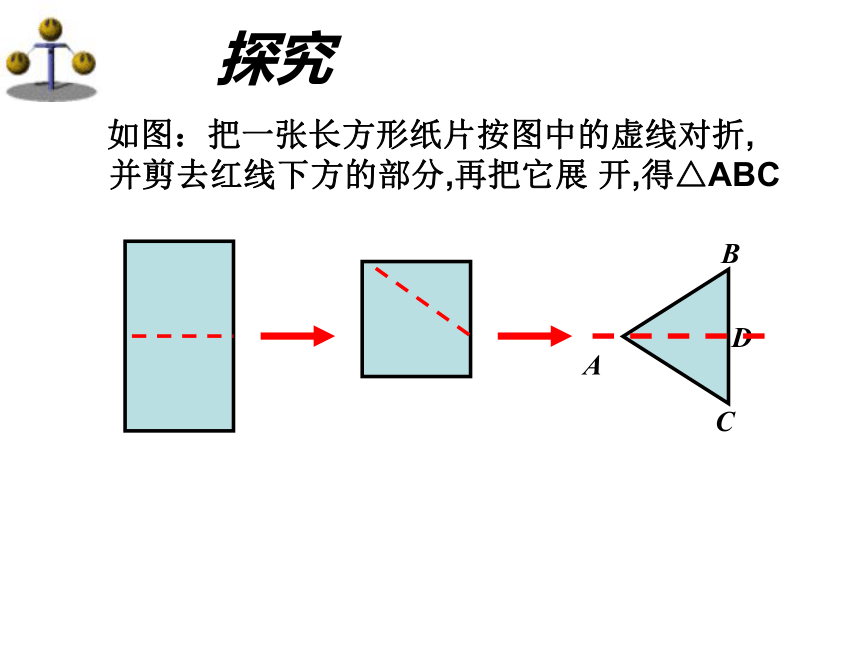
如图:把一张长方形纸片按图中的虚线对折,
并剪去红线下方的部分,再把它展 开,得△ABC
探究
A
C
B
D
A
C
B
腰
腰
底边
底角
底角
顶角
等腰三角形中,相等的两边都叫做腰,
另一边叫做底边,
两腰的夹角叫做顶角,
腰和底边的夹角叫做底角.
等腰三角形的定义及相关概念
像△ABC 这样有两条边相等(AB=AC)
的三角形,叫做等腰三角形.
∠B = ∠C
∠B = ∠C
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
重合的线段 重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠BAD = ∠CAD
∠ADB = ∠ADC
A
B
C
D
探 索 与 证 明
等腰三角形的两个底角相等.
已知:如图,在ΔABC中,AB=AC,
求证:∠B=∠C.
证明:
即时巩固
⒈等腰三角形一个底角为75°,它的另外两个角为_______ .
⒉等腰三角形一个角为70°,它的另外两个角为___________________ .
⒊等腰三角形一个角为120°,它的另外两个角为________ .
75°、30°
70°、40°或55°、55°
30°、30°
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
重合的线段 重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC
BD=CD
∠BAD = ∠CAD
∠ADB = ∠ADC
A
B
C
D
探 索 与 应 用
等腰三角形的顶角平分线、底边中线、底边上的高相互重合.
如右图在△ABC中,当AB=AC时,
(1)若AD⊥BC,
则∠ BAD = ∠____ , CD = ___ ;
(2)若AD是底边BC的中线,
则AD ⊥___ ,∠BAD =∠____ ;
(3)若AD是顶角∠BAD的角平分线,
则AD ⊥___ , BD =___ .
CAD
BC
CAD
BC
CD
BD
学 以 致 用
如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD, (1)图中共有几个等腰三角形?
(2)你能求出△ABC各角的度数吗
解:(1)图中共有3个等腰三角形:
△ABC、 △ABD 、△BDC
(2)设∠A=x,
∵AB=AC, BD=BC=AD,
∴∠ABC=∠ C=∠ BDC, ∠ A=∠ ABD=x,
∴∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C=∠BDC=2x,
在△ABC中,有
∠A+ ∠ABC+ ∠C=x+2x+2x=180°,
解得x=36°
∴在△ABC中, ∠A=360, ∠ABC= ∠C=72°.
C
B
A
x
x
2x
2x
D
有两边相等
定义
归 纳 小 结
A
C
B
腰
腰
底边
底角
底角
顶角
等腰三角形中,相等的两边都叫做腰,
另一边叫做底边,
两腰的夹角叫做顶角,
腰和底边的夹角叫做底角.
等腰三角形的相关概念
像△ABC 这样有两条边相等(AB=AC)
的三角形,叫做等腰三角形.
等边对等角
三线合一
有两边相等
定义
性质
归 纳 小 结
等腰三角形的性质
性质二
等腰三角形的顶角平分线、底边上中线、底边上的高相互重合.(“三线合一”)
性质一
等腰三角形的两个底角相等.
(等边对等角)
必做题:活页P33-34
思考题:在△ABC中,如果∠B= ∠C,那么△ABC是等腰三角形吗?
课 后 延 伸
12.3.1 等腰三角形
如图:把一张长方形纸片按图中的虚线对折,
并剪去红线下方的部分,再把它展 开,得△ABC
探究
A
C
B
D
A
C
B
腰
腰
底边
底角
底角
顶角
等腰三角形中,相等的两边都叫做腰,
另一边叫做底边,
两腰的夹角叫做顶角,
腰和底边的夹角叫做底角.
等腰三角形的定义及相关概念
像△ABC 这样有两条边相等(AB=AC)
的三角形,叫做等腰三角形.
∠B = ∠C
∠B = ∠C
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
重合的线段 重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠BAD = ∠CAD
∠ADB = ∠ADC
A
B
C
D
探 索 与 证 明
等腰三角形的两个底角相等.
已知:如图,在ΔABC中,AB=AC,
求证:∠B=∠C.
证明:
即时巩固
⒈等腰三角形一个底角为75°,它的另外两个角为_______ .
⒉等腰三角形一个角为70°,它的另外两个角为___________________ .
⒊等腰三角形一个角为120°,它的另外两个角为________ .
75°、30°
70°、40°或55°、55°
30°、30°
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
重合的线段 重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC
BD=CD
∠BAD = ∠CAD
∠ADB = ∠ADC
A
B
C
D
探 索 与 应 用
等腰三角形的顶角平分线、底边中线、底边上的高相互重合.
如右图在△ABC中,当AB=AC时,
(1)若AD⊥BC,
则∠ BAD = ∠____ , CD = ___ ;
(2)若AD是底边BC的中线,
则AD ⊥___ ,∠BAD =∠____ ;
(3)若AD是顶角∠BAD的角平分线,
则AD ⊥___ , BD =___ .
CAD
BC
CAD
BC
CD
BD
学 以 致 用
如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD, (1)图中共有几个等腰三角形?
(2)你能求出△ABC各角的度数吗
解:(1)图中共有3个等腰三角形:
△ABC、 △ABD 、△BDC
(2)设∠A=x,
∵AB=AC, BD=BC=AD,
∴∠ABC=∠ C=∠ BDC, ∠ A=∠ ABD=x,
∴∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C=∠BDC=2x,
在△ABC中,有
∠A+ ∠ABC+ ∠C=x+2x+2x=180°,
解得x=36°
∴在△ABC中, ∠A=360, ∠ABC= ∠C=72°.
C
B
A
x
x
2x
2x
D
有两边相等
定义
归 纳 小 结
A
C
B
腰
腰
底边
底角
底角
顶角
等腰三角形中,相等的两边都叫做腰,
另一边叫做底边,
两腰的夹角叫做顶角,
腰和底边的夹角叫做底角.
等腰三角形的相关概念
像△ABC 这样有两条边相等(AB=AC)
的三角形,叫做等腰三角形.
等边对等角
三线合一
有两边相等
定义
性质
归 纳 小 结
等腰三角形的性质
性质二
等腰三角形的顶角平分线、底边上中线、底边上的高相互重合.(“三线合一”)
性质一
等腰三角形的两个底角相等.
(等边对等角)
必做题:活页P33-34
思考题:在△ABC中,如果∠B= ∠C,那么△ABC是等腰三角形吗?
课 后 延 伸
