7.3.2多边形内角和
图片预览



文档简介
(共19张PPT)
§7.3.2多边形的内角和
1.三角形的内角和是多少?
三角形的内角和是180°
2.n边形从一个顶点出发的对角线有 _____条?它们将n边形分成 个三角形?
回 顾
(n-3)
(n-2)
3.你知道长方形和正方形的内角和是多少?其它四边形的内角和是多少?
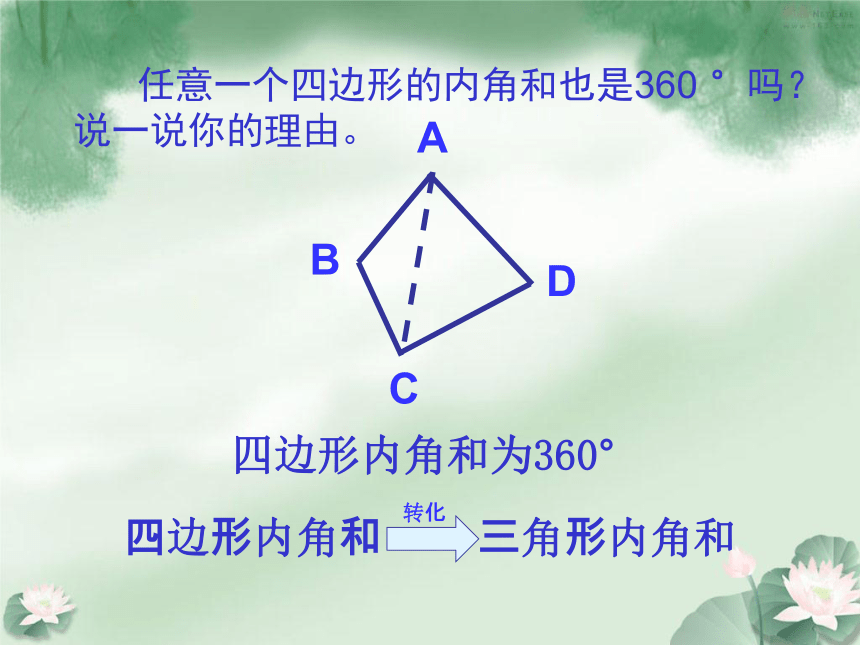
任意一个四边形的内角和也是360 °吗?说一说你的理由。
四边形内角和为360°
四边形内角和 三角形内角和
转化
A
B
C
D
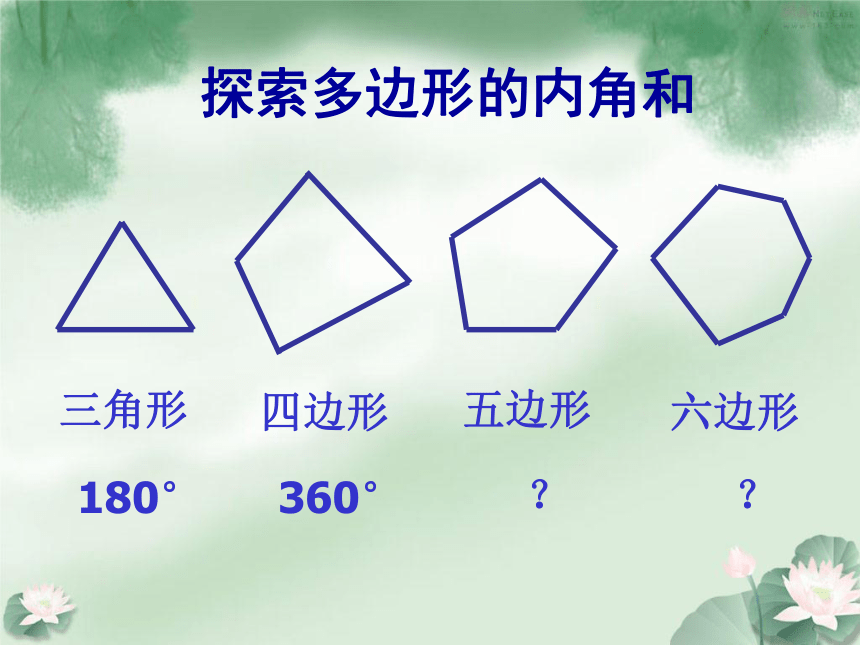
三角形
六边形
四边形
探索多边形的内角和
五边形
180°
360°
?
?
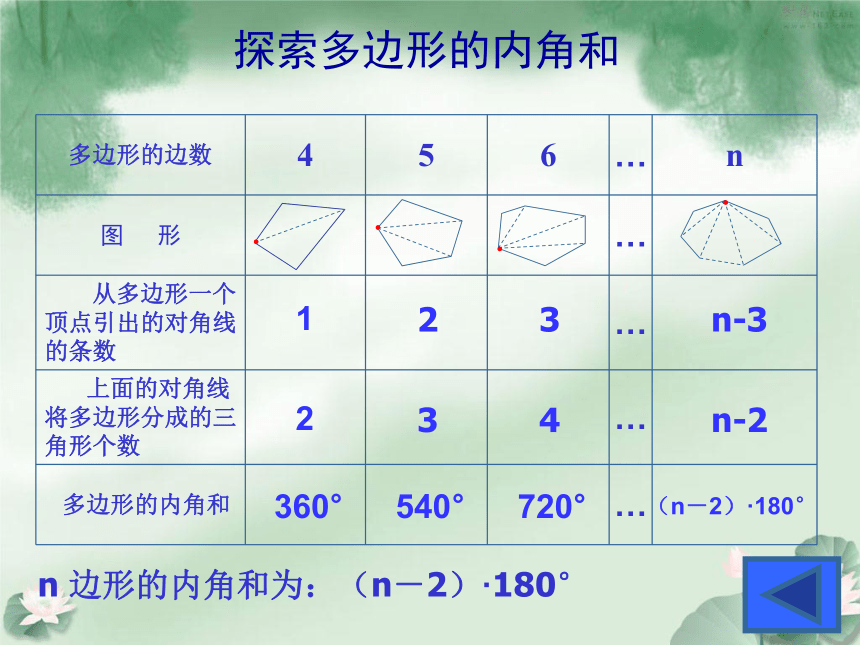
探索多边形的内角和
2
3
n-3
3
n-2
4
n 边形的内角和为:(n-2)·180°
(n-2)·180°
多边形的边数 4 5 6 … n
图 形 …
从多边形一个顶点引出的对角线的条数 …
上面的对角线将多边形分成的三角形个数 …
多边形的内角和 …
720°
540°
360°
1
2
把一个多边形分成几个三角形,还有其他分法吗?由新的分法能得出多边形内角和公式吗?
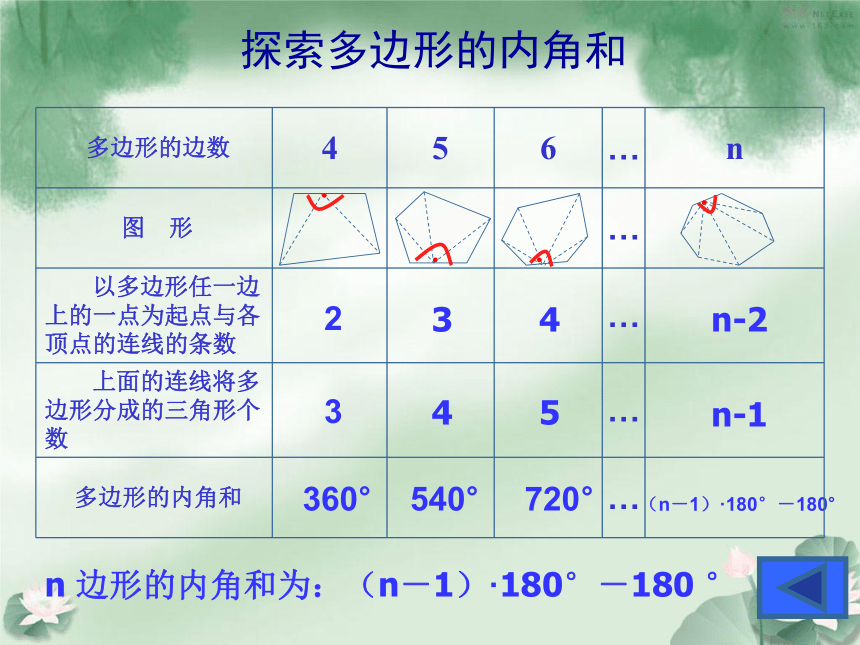
探索多边形的内角和
3
4
n-2
4
n-1
5
n 边形的内角和为:(n-1)·180°-180 °
(n-1)·180°-180°
多边形的边数 4 5 6 … n
图 形 …
以多边形任一边上的一点为起点与各顶点的连线的条数 …
上面的连线将多 边形分成的三角形个数 …
多边形的内角和 …
360°
540°
720°
2
3
探索多边形的内角和
5
n
180 ° ·n-360 °
n 边形的内角和为:180°·n-360°
6
5
6
n
多边形的边数 4 5 6 … n
图 形 …
以多边形内任一点为起点,与各顶点的连线的条数 …
上面的连线将多边形分成的三角形个数 …
多边形的内角和 …
360°
540°
720°
4
4
总 结
n 边形内角和为
(n-2)·180°
(n≥3且为正整数)
例1:一个多边形的内角和为1080°,它是几边形?
解:设这个多边形的边数为n
则(n-2) 180°= 1080°
解得 n = 8
所以这个多边形是八边形。
1、七边形的内角和等于 度;
一个n边形的内角和为1800 ,则n= 。
2、从多边形一个顶点出发可引7条对角线,则这个n边形的内角和为( )
A、1620 B、1800 C、900 D、1440
3、一个多边形边数每增加1条时,其内角和增加( )
A、180 B、360 C、不变 D、不能确定
应用知识解决问题(1)
D
12
900
A
例2: 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和,五边形的外角和等于多少?
解:
五边形外角和=5个平角-五边形内角和
=5×180°-(5-2)×180°
=360°
如果将例2中五边形换为n边形(n≥3且为正整数),可以得到相同结果吗?
解:
n边形外角和=n个平角-n边形内角和
=n×180°- (n-2) × 180°
=360°
结论:多边形的外角和等于360°
1、正五边形的每一个外角等于____,每一个内角等于_____。
应用知识解决问题(2)
解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:
5X=360°
X=72°
∴ 每一个内角度数为108 °
72°
108°
2、已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。
解: 设多边形的边数为n
∵它的内角和等于 (n-2) 180°,
多边形外角和等于360 ,
∴ (n-2) 180°=2× 360 。
解得: n=6
∴这个多边形的边数为6。
课 时 小 结
1、这节课你掌握了哪些新知识?
2、你学会了哪些重要方法?有什么启示?
(1)这节课我们主要学习了多边形的内角和公式 (n-2) · 180°
(2)多边形的外角和为 360 °
(3) 类比,转化的数学思想方法;从不同的角度思考问题可以得到解决问题的不同方法。
课 后 作 业
必做题:课本第85页
第4、5、6、7题
选做题:课本第85页第9题
探 究
把一块四边形的木料锯掉一个角后,所得的多边形的内角和为多少度?
§7.3.2多边形的内角和
1.三角形的内角和是多少?
三角形的内角和是180°
2.n边形从一个顶点出发的对角线有 _____条?它们将n边形分成 个三角形?
回 顾
(n-3)
(n-2)
3.你知道长方形和正方形的内角和是多少?其它四边形的内角和是多少?
任意一个四边形的内角和也是360 °吗?说一说你的理由。
四边形内角和为360°
四边形内角和 三角形内角和
转化
A
B
C
D
三角形
六边形
四边形
探索多边形的内角和
五边形
180°
360°
?
?
探索多边形的内角和
2
3
n-3
3
n-2
4
n 边形的内角和为:(n-2)·180°
(n-2)·180°
多边形的边数 4 5 6 … n
图 形 …
从多边形一个顶点引出的对角线的条数 …
上面的对角线将多边形分成的三角形个数 …
多边形的内角和 …
720°
540°
360°
1
2
把一个多边形分成几个三角形,还有其他分法吗?由新的分法能得出多边形内角和公式吗?
探索多边形的内角和
3
4
n-2
4
n-1
5
n 边形的内角和为:(n-1)·180°-180 °
(n-1)·180°-180°
多边形的边数 4 5 6 … n
图 形 …
以多边形任一边上的一点为起点与各顶点的连线的条数 …
上面的连线将多 边形分成的三角形个数 …
多边形的内角和 …
360°
540°
720°
2
3
探索多边形的内角和
5
n
180 ° ·n-360 °
n 边形的内角和为:180°·n-360°
6
5
6
n
多边形的边数 4 5 6 … n
图 形 …
以多边形内任一点为起点,与各顶点的连线的条数 …
上面的连线将多边形分成的三角形个数 …
多边形的内角和 …
360°
540°
720°
4
4
总 结
n 边形内角和为
(n-2)·180°
(n≥3且为正整数)
例1:一个多边形的内角和为1080°,它是几边形?
解:设这个多边形的边数为n
则(n-2) 180°= 1080°
解得 n = 8
所以这个多边形是八边形。
1、七边形的内角和等于 度;
一个n边形的内角和为1800 ,则n= 。
2、从多边形一个顶点出发可引7条对角线,则这个n边形的内角和为( )
A、1620 B、1800 C、900 D、1440
3、一个多边形边数每增加1条时,其内角和增加( )
A、180 B、360 C、不变 D、不能确定
应用知识解决问题(1)
D
12
900
A
例2: 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和,五边形的外角和等于多少?
解:
五边形外角和=5个平角-五边形内角和
=5×180°-(5-2)×180°
=360°
如果将例2中五边形换为n边形(n≥3且为正整数),可以得到相同结果吗?
解:
n边形外角和=n个平角-n边形内角和
=n×180°- (n-2) × 180°
=360°
结论:多边形的外角和等于360°
1、正五边形的每一个外角等于____,每一个内角等于_____。
应用知识解决问题(2)
解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:
5X=360°
X=72°
∴ 每一个内角度数为108 °
72°
108°
2、已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。
解: 设多边形的边数为n
∵它的内角和等于 (n-2) 180°,
多边形外角和等于360 ,
∴ (n-2) 180°=2× 360 。
解得: n=6
∴这个多边形的边数为6。
课 时 小 结
1、这节课你掌握了哪些新知识?
2、你学会了哪些重要方法?有什么启示?
(1)这节课我们主要学习了多边形的内角和公式 (n-2) · 180°
(2)多边形的外角和为 360 °
(3) 类比,转化的数学思想方法;从不同的角度思考问题可以得到解决问题的不同方法。
课 后 作 业
必做题:课本第85页
第4、5、6、7题
选做题:课本第85页第9题
探 究
把一块四边形的木料锯掉一个角后,所得的多边形的内角和为多少度?
