2020-2021学年华东师大版七年级下册第九章《多边形》本章测试(Word版 含答案)
文档属性
| 名称 | 2020-2021学年华东师大版七年级下册第九章《多边形》本章测试(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 108.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 00:00:00 | ||
图片预览

文档简介
第九章《多边形》本章检测
满分:100分,限时:60分钟
一、选择题(每题3分,共30分)
1.四边形不具有稳定性,当四边形形状改变时,发生变化的是(
)
A.四边形的边长
B.四边形的周长
C.四边形的某些角的大小
D.四边形的内角和
2.一个多边形的每个内角均为120°,则这个多边形是(
)
A.四边形
B.五边形
C.六边形
D.七边形
3.若一个多边形每一个内角都是135?,则这个多边形的边数是
(
)
A.6
B.8
C.10
D.12
4.将一个n边形变成(n+1)边形,内角和将( )
A.减少180°
B.增加90°
C.增加180°
D.增加360°
5.阳光中学阅览室在装修过程中,准备用边长相等的正方形和正三角形两种地砖镶嵌地面,在每个顶点的周围正方形、正三角形地砖的块数可以分别是(
)
A.2,2
B.2,3
C.1,2
D.2,1
6.若一个三角形的两边长分别为5和8,则第三边长可能是( )
A.14
B.10
C.3
D.2
7.将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是(???
).
A.45°
B.60°
C.75°
D.85°
8.已知a、b、c是△ABC的三条边长,化简|a+b-c|-|c-a-b|的结果为(
)
A.2a+2b-2c
B.2a+2b
C.2c
D.0
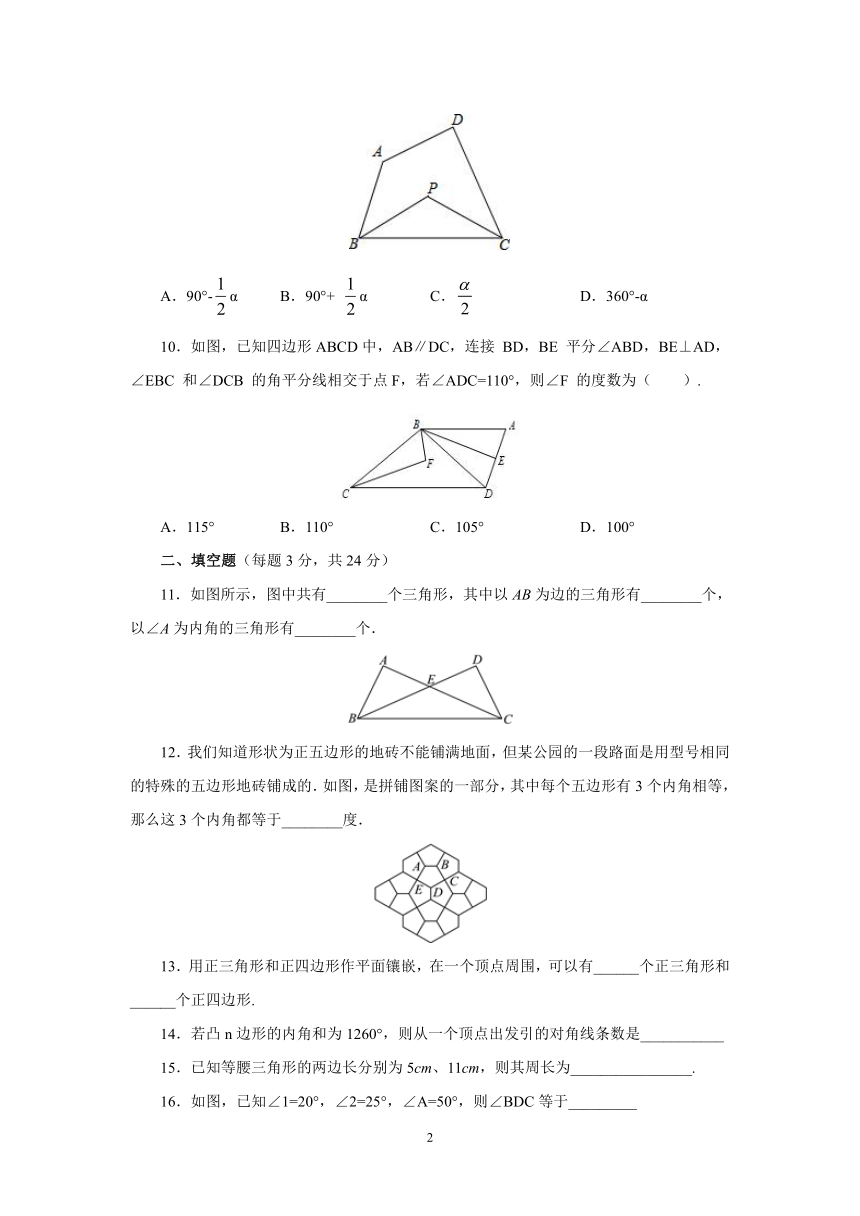
9.如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=( )
A.90°-α
B.90°+
α
C.
D.360°-α
10.如图,已知四边形ABCD中,AB∥DC,连接
BD,BE
平分∠ABD,BE⊥AD,∠EBC
和∠DCB
的角平分线相交于点F,若∠ADC=110°,则∠F
的度数为(
).
A.115°
B.110°
C.105°
D.100°
二、填空题(每题3分,共24分)
11.如图所示,图中共有________个三角形,其中以AB为边的三角形有________个,以∠A为内角的三角形有________个.
12.我们知道形状为正五边形的地砖不能铺满地面,但某公园的一段路面是用型号相同的特殊的五边形地砖铺成的.如图,是拼铺图案的一部分,其中每个五边形有3个内角相等,那么这3个内角都等于________度.
13.用正三角形和正四边形作平面镶嵌,在一个顶点周围,可以有______个正三角形和______个正四边形.
14.若凸n边形的内角和为1260°,则从一个顶点出发引的对角线条数是___________
15.已知等腰三角形的两边长分别为5cm、11cm,则其周长为________________.
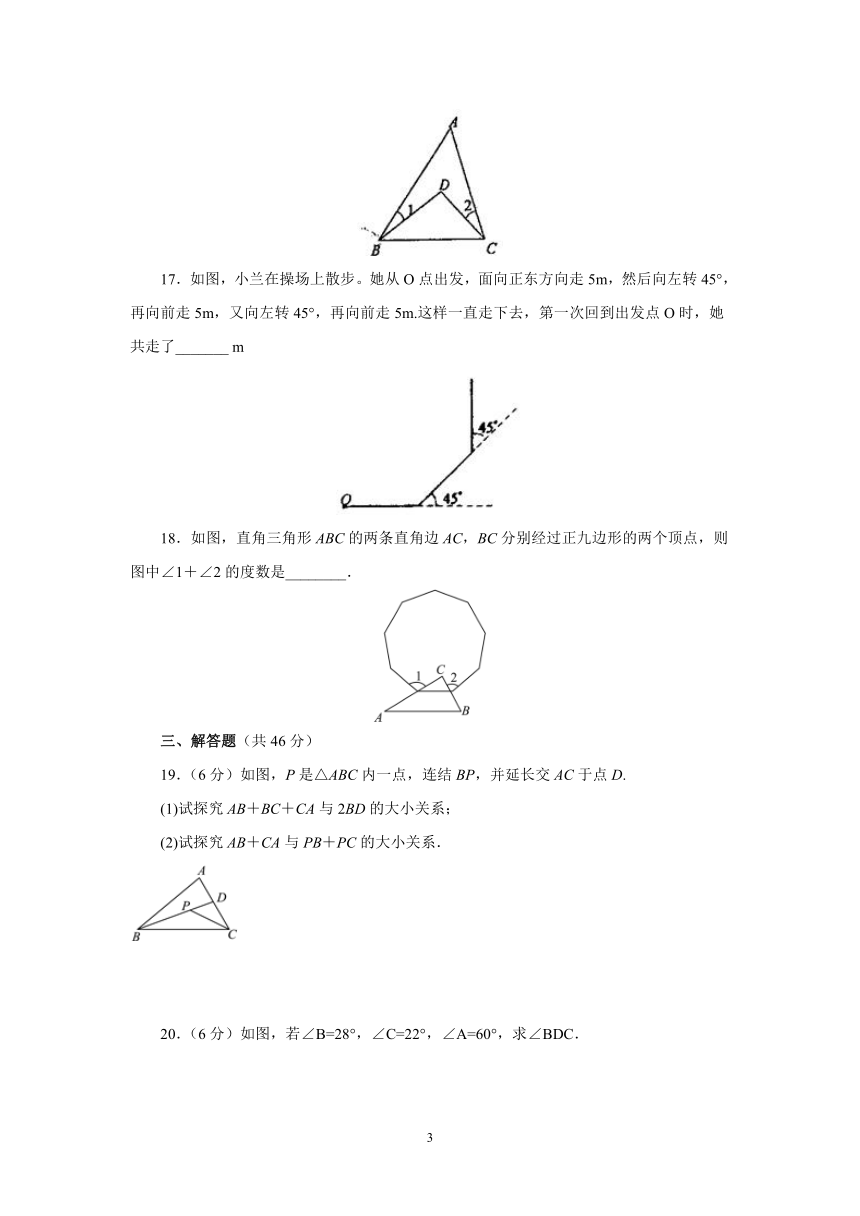
16.如图,已知∠1=20°,∠2=25°,∠A=50°,则∠BDC等于_________
17.如图,小兰在操场上散步。她从O点出发,面向正东方向走5m,然后向左转45°,再向前走5m,又向左转45°,再向前走5m.这样一直走下去,第一次回到出发点O时,她共走了_______
m
18.如图,直角三角形ABC的两条直角边AC,BC分别经过正九边形的两个顶点,则图中∠1+∠2的度数是________.
三、解答题(共46分)
19.(6分)如图,P是△ABC内一点,连结BP,并延长交AC于点D.
(1)试探究AB+BC+CA与2BD的大小关系;
(2)试探究AB+CA与PB+PC的大小关系.
20.(6分)如图,若∠B=28°,∠C=22°,∠A=60°,求∠BDC.
21.(6分)如图,以五边形的五个顶点为圆心画图,半径均为2cm,求图中阴影部分的面积之和.(x取3.14)
22.(6分)如图,△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=152°,求∠A的度数.
23.(6分)(1)如图①所示,∠1+∠2与∠B+∠C有什么关系?为什么?
(2)如图②若把△ABC纸片沿DE点折叠当点A落在四边形BCED内部时,则∠A与∠α+∠β之间有一种数量关系始终保持不变,请写出这个规律并说明理由.
24.(8分)已知:如图,在四边形ABCD中,∠D=90°,∠ABC=∠BCD,点E在直线BC上,点F在直线CD上,且∠AEB=∠CEF.
(1)如图20①,若AE平分∠BAD,求证:EF⊥AE;
(2)如图20②,若AE平分四边形ABCD的外角,其余条件不变,则(1)中的结论是否仍然成立?并说明理由.
25.(8分)如图①,△ABC中,∠ABC与∠ACB的平分线交于点I.根据下列条件,求∠BIC的
度数。
(1)若∠ABC=60°,∠ACB=70°,则∠BIC=
(2)若∠ABC+∠ACB=130°,则∠BIC=
(3)若∠A=50°,则∠BIC=
(4)若∠A=110°,则∠BIC=
(5)从上述计算中,我们能发现已知∠A,求∠BIC的公式是:∠BIC=
.
(6)如图②,BP,CP分别是∠ABC与∠ACB的外角平分线,交于点P.
若已知∠A,则求∠BPC的公式是:∠BPC=
参考答案
1.C
2.C
3.B
4.C
5.B
6.B
7.C
8.D
9.C
10.D
11.5
2
2
12.120
13.3,2
14.6
15.27cm
16.95
17.40
18.190°
19.(1)AB+BC+CA>2BD;(2)AB+CA>PB+PC.
20.∠BDC=110°.
21.18.84cm2
22.∠A=56°.
23.(1)∠1+∠2=∠B+∠C;(2)规律:α+β=2∠A.理由略
24.(1)
略;(2)
EF⊥AE仍成立,理由略.
25.(1)115°;(2)115°;(3)115°(4)145°(5)90°+∠A:(6)90°-∠A.
满分:100分,限时:60分钟
一、选择题(每题3分,共30分)
1.四边形不具有稳定性,当四边形形状改变时,发生变化的是(
)
A.四边形的边长
B.四边形的周长
C.四边形的某些角的大小
D.四边形的内角和
2.一个多边形的每个内角均为120°,则这个多边形是(
)
A.四边形
B.五边形
C.六边形
D.七边形
3.若一个多边形每一个内角都是135?,则这个多边形的边数是
(
)
A.6
B.8
C.10
D.12
4.将一个n边形变成(n+1)边形,内角和将( )
A.减少180°
B.增加90°
C.增加180°
D.增加360°
5.阳光中学阅览室在装修过程中,准备用边长相等的正方形和正三角形两种地砖镶嵌地面,在每个顶点的周围正方形、正三角形地砖的块数可以分别是(
)
A.2,2
B.2,3
C.1,2
D.2,1
6.若一个三角形的两边长分别为5和8,则第三边长可能是( )
A.14
B.10
C.3
D.2
7.将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是(???
).
A.45°
B.60°
C.75°
D.85°
8.已知a、b、c是△ABC的三条边长,化简|a+b-c|-|c-a-b|的结果为(
)
A.2a+2b-2c
B.2a+2b
C.2c
D.0
9.如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=( )
A.90°-α
B.90°+
α
C.
D.360°-α
10.如图,已知四边形ABCD中,AB∥DC,连接
BD,BE
平分∠ABD,BE⊥AD,∠EBC
和∠DCB
的角平分线相交于点F,若∠ADC=110°,则∠F
的度数为(
).
A.115°
B.110°
C.105°
D.100°
二、填空题(每题3分,共24分)
11.如图所示,图中共有________个三角形,其中以AB为边的三角形有________个,以∠A为内角的三角形有________个.
12.我们知道形状为正五边形的地砖不能铺满地面,但某公园的一段路面是用型号相同的特殊的五边形地砖铺成的.如图,是拼铺图案的一部分,其中每个五边形有3个内角相等,那么这3个内角都等于________度.
13.用正三角形和正四边形作平面镶嵌,在一个顶点周围,可以有______个正三角形和______个正四边形.
14.若凸n边形的内角和为1260°,则从一个顶点出发引的对角线条数是___________
15.已知等腰三角形的两边长分别为5cm、11cm,则其周长为________________.
16.如图,已知∠1=20°,∠2=25°,∠A=50°,则∠BDC等于_________
17.如图,小兰在操场上散步。她从O点出发,面向正东方向走5m,然后向左转45°,再向前走5m,又向左转45°,再向前走5m.这样一直走下去,第一次回到出发点O时,她共走了_______
m
18.如图,直角三角形ABC的两条直角边AC,BC分别经过正九边形的两个顶点,则图中∠1+∠2的度数是________.
三、解答题(共46分)
19.(6分)如图,P是△ABC内一点,连结BP,并延长交AC于点D.
(1)试探究AB+BC+CA与2BD的大小关系;
(2)试探究AB+CA与PB+PC的大小关系.
20.(6分)如图,若∠B=28°,∠C=22°,∠A=60°,求∠BDC.
21.(6分)如图,以五边形的五个顶点为圆心画图,半径均为2cm,求图中阴影部分的面积之和.(x取3.14)
22.(6分)如图,△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=152°,求∠A的度数.
23.(6分)(1)如图①所示,∠1+∠2与∠B+∠C有什么关系?为什么?
(2)如图②若把△ABC纸片沿DE点折叠当点A落在四边形BCED内部时,则∠A与∠α+∠β之间有一种数量关系始终保持不变,请写出这个规律并说明理由.
24.(8分)已知:如图,在四边形ABCD中,∠D=90°,∠ABC=∠BCD,点E在直线BC上,点F在直线CD上,且∠AEB=∠CEF.
(1)如图20①,若AE平分∠BAD,求证:EF⊥AE;
(2)如图20②,若AE平分四边形ABCD的外角,其余条件不变,则(1)中的结论是否仍然成立?并说明理由.
25.(8分)如图①,△ABC中,∠ABC与∠ACB的平分线交于点I.根据下列条件,求∠BIC的
度数。
(1)若∠ABC=60°,∠ACB=70°,则∠BIC=
(2)若∠ABC+∠ACB=130°,则∠BIC=
(3)若∠A=50°,则∠BIC=
(4)若∠A=110°,则∠BIC=
(5)从上述计算中,我们能发现已知∠A,求∠BIC的公式是:∠BIC=
.
(6)如图②,BP,CP分别是∠ABC与∠ACB的外角平分线,交于点P.
若已知∠A,则求∠BPC的公式是:∠BPC=
参考答案
1.C
2.C
3.B
4.C
5.B
6.B
7.C
8.D
9.C
10.D
11.5
2
2
12.120
13.3,2
14.6
15.27cm
16.95
17.40
18.190°
19.(1)AB+BC+CA>2BD;(2)AB+CA>PB+PC.
20.∠BDC=110°.
21.18.84cm2
22.∠A=56°.
23.(1)∠1+∠2=∠B+∠C;(2)规律:α+β=2∠A.理由略
24.(1)
略;(2)
EF⊥AE仍成立,理由略.
25.(1)115°;(2)115°;(3)115°(4)145°(5)90°+∠A:(6)90°-∠A.
