平行四边形的性质
图片预览





文档简介
(共21张PPT)
教学目标:
1、通过认识平行四边形的形象,学习平行四边形的 概念。
2、经历探索平行四边形的性质的过程。
3、能利用平行四边形的定义和性质解决有关问题。
4、在活动中发展学生的探究意识和合作交流的习惯。
大家知道什么样的四边形叫平行四形吗?
定义:
记作:
几何语言:
∴四边形ABCD是平行四边形.
ABCD
在四边形ABCD中,
读作:平行四边形ABCD
平行四边形中,相邻的边、角分别简称为
反之:
∴ AB∥CD,AD∥BC
A
B
D
C
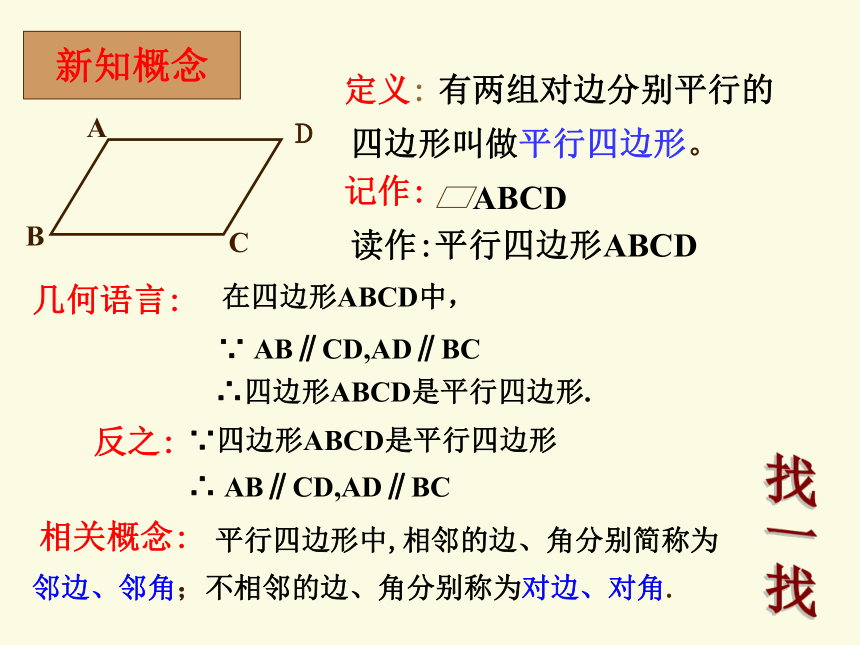
有两组对边分别平行的
四边形叫做平行四边形。
新知概念
∵ AB∥CD,AD∥BC
∵四边形ABCD是平行四边形
相关概念:
邻边、邻角;不相邻的边、角分别称为对边、对角.
A
B
C
D
O
O
A
B
C
D
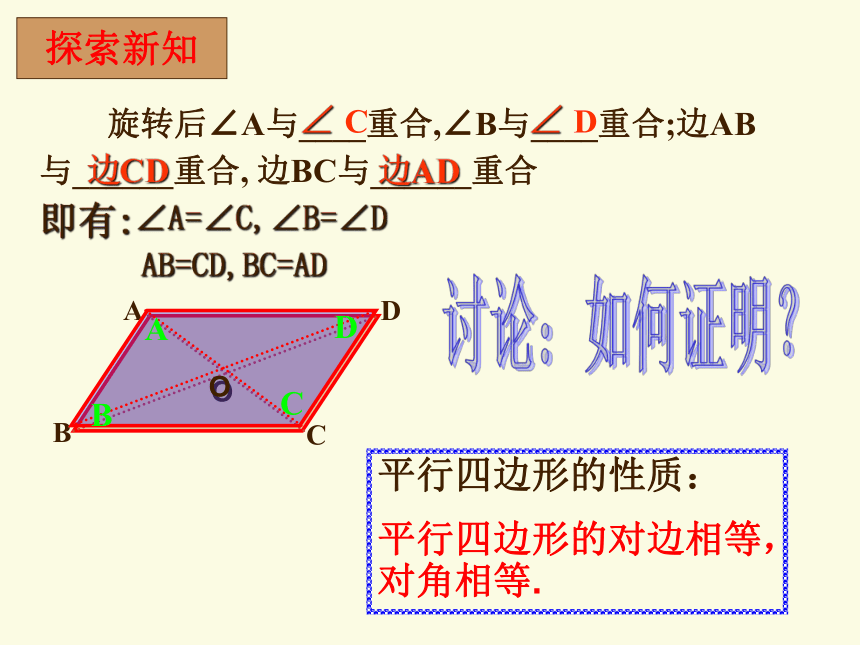
旋转后∠A与____重合,∠B与____重合;边AB
与______重合, 边BC与______重合
∠ C
∠ D
边CD
边AD
平行四边形的性质:
平行四边形的对边相等,对角相等.
探索新知
即有:
∠A=∠C,∠B=∠D
AB=CD,BC=AD
已知: ABCD(如图)
求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB
即∠BAD=∠DCB
证明:连结AC
∵AB∥CD,AD∥BC(平行四边形的对边平行)
∴∠1=∠2,∠3=∠4
∠1=∠2,AC=CA,∠3=∠4
∴ ABC≌ CDA(ASA)
∴AB=CD,BC=DA,∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在 ABC和 CDA中
A
B
C
D
1
2
3
4
平行四边形的邻角互补.
A
B
C
D
几何语言:
∵四边形ABCD是平行四边形
∴ AB∥CD,AD∥BC
平行四边形的对边平行.
平行四边形的对边相等.
∵四边形ABCD是平行四边形
∴ AB=CD,BC=DA
平行四边形的对角相等.
∵四边形ABCD是平行四边形
∴ ∠A=∠C,∠B=∠D
∵四边形ABCD是平行四边形
∴ ∠A+∠B=180°, ∠B+∠C=180°,
1.填空:
如图, ABCD, 则AB//_____,
AD//_____, AB=____, BC=_____,
∠A=_____, ∠B =_____。
∠A+____________ =180°。
CD
BC
CD
AD
∠C
∠D
∠B ( ∠D )
2.如图:在 ABCD中,根据已知你能得到哪
些结论?为什么
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
例题教学:
例1 如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
解:
∵四边形ABCD是平行四边形
∵AB=8m
8m
训练1
在 ABCD中,
⑴
∠A=40°,
A
B
C
D
则∠C= ____, ∠B= ______.
40°
140°
在 ABCD中,
⑵
若∠A+∠C= 80°,
则四个内角的度数为: _____________________.
40°
、140°
、40°
、140°
在 ABCD中,
⑶
已知∠B-∠C= 80°,
求它的四个内角的度数.
解:
在 ABCD中,
∵AB∥CD
∴∠B+∠C= 180°
又∵∠B-∠C= 80°,
解得:∠B= 130°, ∠C=50°
∴∠D= 130°, ∠A=50°
训练2
在 ABCD中,
⑴
A
B
C
D
AB=8, BC=4, 则CD= ___,
8
四边形的周长是_____.
24
已知 ABCD的周长等
⑵
于24, 则AB+BC= ___ ,又AB=8,则AD= ___.
12
4
在 ABCD中,
⑶
已知其周长为40cm,且,边AB
比边BC长2cm,求四边形各边的长.
解:
在 ABCD中,
AB=CD, AD=BC
∵AB+BC+CD+AD=40
∴AB+BC=20
又∵AB-BC=2
解得: AB=11
解得: BC=9
∴ CD=11,AD=9.
1.平行四边形ABCD中,若在AD上取一点E,
CB上取一点F,且AE=CF,试测量比较BE ,DF的大小并说明理由。
A
B
D
C
能力挑战
F
E
证明:
∵四边形ABCD是平行四边形
∴ AB=CD, ∠A=∠C
在 ABC和 CDA中
∵ AB=CD
∠A=∠C
AE=CF
∴ ABC≌ CDA(SAS)
∴ BE=DF
2、在 ABCD 中, DB=DC, ∠C=70°,AE⊥BD于E,求∠DAE和 ∠BAE的度数
70°
解∵四边形ABCD是平行四边形
∴ ∠DAB=∠C= 70°
∵ DB=DC
∴ ∠CBD=∠C=70 °
∵ DA∥BC
∴ ∠ADB=∠CBD= 70 °
A
B
C
D
E
∵ AE⊥BD
∴ ∠DEA=90°
∴ ∠DAE=20°
∴ ∠BAE=50°
能力挑战
ABCD
② 角
① 边
对边平行且相等
对角相等
邻角互补
知识点(一):定义及表示方法
知识点(二):性质
1. 课本84页练习1、2、3
2. 练习册78页第一课时
教学目标:
1、通过认识平行四边形的形象,学习平行四边形的 概念。
2、经历探索平行四边形的性质的过程。
3、能利用平行四边形的定义和性质解决有关问题。
4、在活动中发展学生的探究意识和合作交流的习惯。
大家知道什么样的四边形叫平行四形吗?
定义:
记作:
几何语言:
∴四边形ABCD是平行四边形.
ABCD
在四边形ABCD中,
读作:平行四边形ABCD
平行四边形中,相邻的边、角分别简称为
反之:
∴ AB∥CD,AD∥BC
A
B
D
C
有两组对边分别平行的
四边形叫做平行四边形。
新知概念
∵ AB∥CD,AD∥BC
∵四边形ABCD是平行四边形
相关概念:
邻边、邻角;不相邻的边、角分别称为对边、对角.
A
B
C
D
O
O
A
B
C
D
旋转后∠A与____重合,∠B与____重合;边AB
与______重合, 边BC与______重合
∠ C
∠ D
边CD
边AD
平行四边形的性质:
平行四边形的对边相等,对角相等.
探索新知
即有:
∠A=∠C,∠B=∠D
AB=CD,BC=AD
已知: ABCD(如图)
求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB
即∠BAD=∠DCB
证明:连结AC
∵AB∥CD,AD∥BC(平行四边形的对边平行)
∴∠1=∠2,∠3=∠4
∠1=∠2,AC=CA,∠3=∠4
∴ ABC≌ CDA(ASA)
∴AB=CD,BC=DA,∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在 ABC和 CDA中
A
B
C
D
1
2
3
4
平行四边形的邻角互补.
A
B
C
D
几何语言:
∵四边形ABCD是平行四边形
∴ AB∥CD,AD∥BC
平行四边形的对边平行.
平行四边形的对边相等.
∵四边形ABCD是平行四边形
∴ AB=CD,BC=DA
平行四边形的对角相等.
∵四边形ABCD是平行四边形
∴ ∠A=∠C,∠B=∠D
∵四边形ABCD是平行四边形
∴ ∠A+∠B=180°, ∠B+∠C=180°,
1.填空:
如图, ABCD, 则AB//_____,
AD//_____, AB=____, BC=_____,
∠A=_____, ∠B =_____。
∠A+____________ =180°。
CD
BC
CD
AD
∠C
∠D
∠B ( ∠D )
2.如图:在 ABCD中,根据已知你能得到哪
些结论?为什么
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
例题教学:
例1 如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
解:
∵四边形ABCD是平行四边形
∵AB=8m
8m
训练1
在 ABCD中,
⑴
∠A=40°,
A
B
C
D
则∠C= ____, ∠B= ______.
40°
140°
在 ABCD中,
⑵
若∠A+∠C= 80°,
则四个内角的度数为: _____________________.
40°
、140°
、40°
、140°
在 ABCD中,
⑶
已知∠B-∠C= 80°,
求它的四个内角的度数.
解:
在 ABCD中,
∵AB∥CD
∴∠B+∠C= 180°
又∵∠B-∠C= 80°,
解得:∠B= 130°, ∠C=50°
∴∠D= 130°, ∠A=50°
训练2
在 ABCD中,
⑴
A
B
C
D
AB=8, BC=4, 则CD= ___,
8
四边形的周长是_____.
24
已知 ABCD的周长等
⑵
于24, 则AB+BC= ___ ,又AB=8,则AD= ___.
12
4
在 ABCD中,
⑶
已知其周长为40cm,且,边AB
比边BC长2cm,求四边形各边的长.
解:
在 ABCD中,
AB=CD, AD=BC
∵AB+BC+CD+AD=40
∴AB+BC=20
又∵AB-BC=2
解得: AB=11
解得: BC=9
∴ CD=11,AD=9.
1.平行四边形ABCD中,若在AD上取一点E,
CB上取一点F,且AE=CF,试测量比较BE ,DF的大小并说明理由。
A
B
D
C
能力挑战
F
E
证明:
∵四边形ABCD是平行四边形
∴ AB=CD, ∠A=∠C
在 ABC和 CDA中
∵ AB=CD
∠A=∠C
AE=CF
∴ ABC≌ CDA(SAS)
∴ BE=DF
2、在 ABCD 中, DB=DC, ∠C=70°,AE⊥BD于E,求∠DAE和 ∠BAE的度数
70°
解∵四边形ABCD是平行四边形
∴ ∠DAB=∠C= 70°
∵ DB=DC
∴ ∠CBD=∠C=70 °
∵ DA∥BC
∴ ∠ADB=∠CBD= 70 °
A
B
C
D
E
∵ AE⊥BD
∴ ∠DEA=90°
∴ ∠DAE=20°
∴ ∠BAE=50°
能力挑战
ABCD
② 角
① 边
对边平行且相等
对角相等
邻角互补
知识点(一):定义及表示方法
知识点(二):性质
1. 课本84页练习1、2、3
2. 练习册78页第一课时
