7.4课题学习_镶嵌课件
文档属性
| 名称 | 7.4课题学习_镶嵌课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 275.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-26 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
7.4 课题学习 镶嵌
镶嵌: 用形状相同或不同的平面封闭图形把一块 地既无缝隙又不重叠地全部覆盖,在几何里
叫做平面镶嵌。
如果让你设计几种地板图案,你会怎么做?
问题1:如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面?
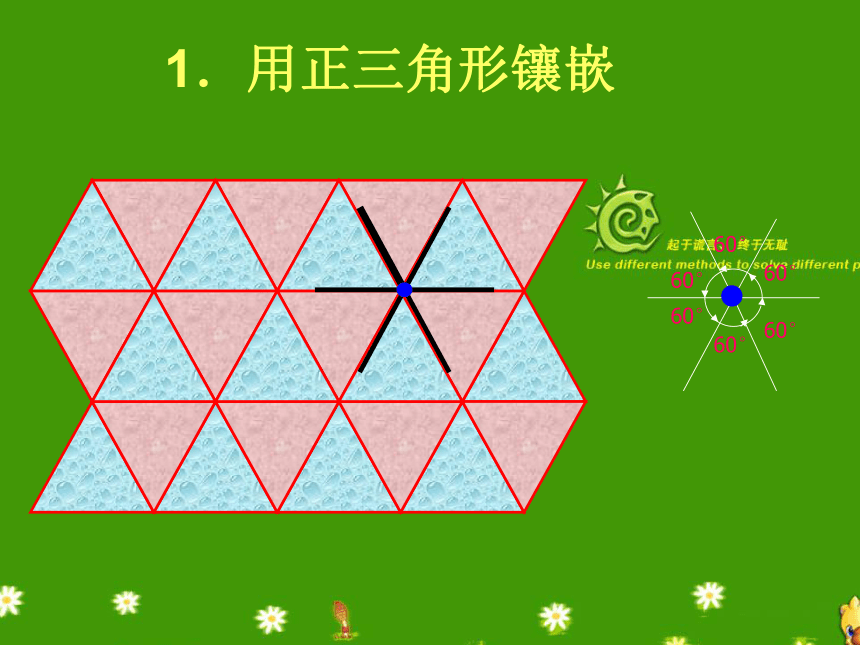
1.用正三角形镶嵌
60°
60°
60°
60°
60°
60°
(2) 正方形的平面镶嵌
90°
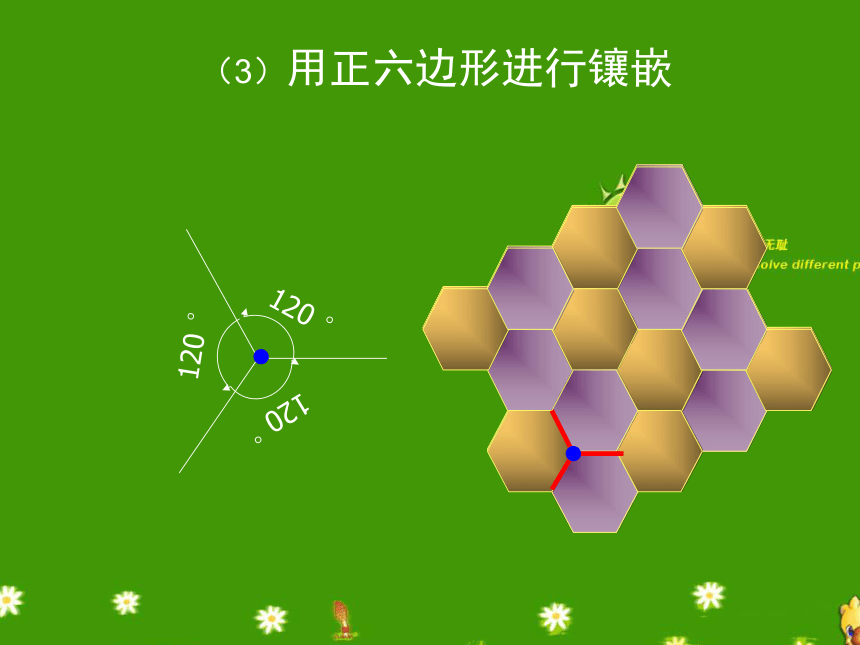
120 °
120 °
120 °
(3)用正六边形进行镶嵌
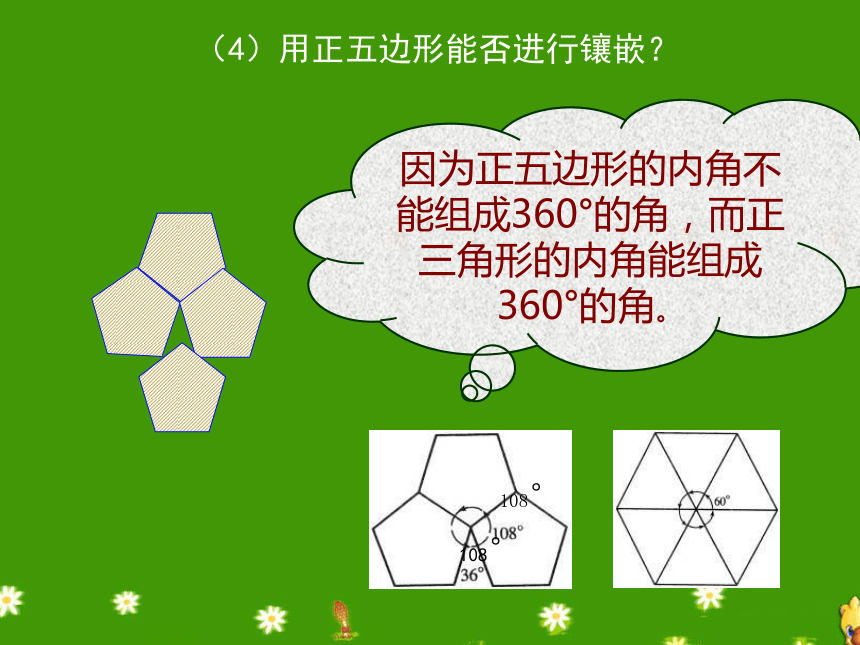
因为正五边形的内角不能组成360°的角,而正三角形的内角能组成360°的角。
(4)用正五边形能否进行镶嵌?
108°
108°
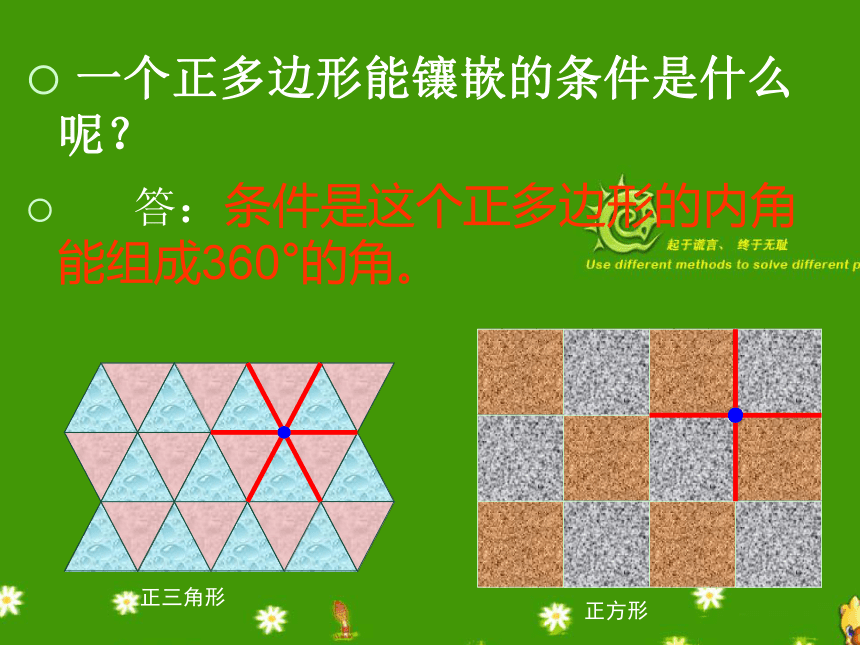
一个正多边形能镶嵌的条件是什么呢?
答:条件是这个正多边形的内角能组成360°的角。
正三角形
正方形
问题1:如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面?
答:正三角形、正方形、正六边形
理由:这些正多边形的内角能组成360°
的角
①
②
1.正方形和正三角形
问题2 :如果允许用几种正多边形组合起来镶嵌(讨论顶点与顶点重合的情况),由哪几种正多边形组合起来能镶嵌成一个平面?
120°
120°
60°
60°
图案(Ⅰ)
每个顶点处正三角形2个,正六边形2个。
图案(Ⅱ)
60°
60°
120°
60°
60°
每个顶点处正六边形1个,正三角形4个.
正十二边形与正三角形的平面镶嵌
正十二边形与正方形、正五边形的平面镶嵌
正八边形与正方形的平面镶嵌
小结
一种正多边形或几种正多边形组合能否镶嵌的条件是:在每个顶点处的内角能否组成360°的角。
练习题
1.能够用一种正多边形铺满地面的是____。 A 正五边形 B 正六边形
C 正七边形 D 正八边形
2.如果用正三角形进行镶嵌,那么在每个顶 点的周围有____个正三角形。
3.如果用正三角形和正六边形进行镶嵌,那 么在每个顶点的周围有____ 个正三角形和____个正六边形 或 ____个正三角形和____ 个正六边形
思考题
1.形状相同的任意三角形能否进行镶嵌?自己动手做一做。
2.形状相同的任意四边形呢?
7.4 课题学习 镶嵌
镶嵌: 用形状相同或不同的平面封闭图形把一块 地既无缝隙又不重叠地全部覆盖,在几何里
叫做平面镶嵌。
如果让你设计几种地板图案,你会怎么做?
问题1:如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面?
1.用正三角形镶嵌
60°
60°
60°
60°
60°
60°
(2) 正方形的平面镶嵌
90°
120 °
120 °
120 °
(3)用正六边形进行镶嵌
因为正五边形的内角不能组成360°的角,而正三角形的内角能组成360°的角。
(4)用正五边形能否进行镶嵌?
108°
108°
一个正多边形能镶嵌的条件是什么呢?
答:条件是这个正多边形的内角能组成360°的角。
正三角形
正方形
问题1:如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面?
答:正三角形、正方形、正六边形
理由:这些正多边形的内角能组成360°
的角
①
②
1.正方形和正三角形
问题2 :如果允许用几种正多边形组合起来镶嵌(讨论顶点与顶点重合的情况),由哪几种正多边形组合起来能镶嵌成一个平面?
120°
120°
60°
60°
图案(Ⅰ)
每个顶点处正三角形2个,正六边形2个。
图案(Ⅱ)
60°
60°
120°
60°
60°
每个顶点处正六边形1个,正三角形4个.
正十二边形与正三角形的平面镶嵌
正十二边形与正方形、正五边形的平面镶嵌
正八边形与正方形的平面镶嵌
小结
一种正多边形或几种正多边形组合能否镶嵌的条件是:在每个顶点处的内角能否组成360°的角。
练习题
1.能够用一种正多边形铺满地面的是____。 A 正五边形 B 正六边形
C 正七边形 D 正八边形
2.如果用正三角形进行镶嵌,那么在每个顶 点的周围有____个正三角形。
3.如果用正三角形和正六边形进行镶嵌,那 么在每个顶点的周围有____ 个正三角形和____个正六边形 或 ____个正三角形和____ 个正六边形
思考题
1.形状相同的任意三角形能否进行镶嵌?自己动手做一做。
2.形状相同的任意四边形呢?
