1、3、3函数的最值与导数

(共13张PPT)
授课班级：高二（7）班
主讲人：
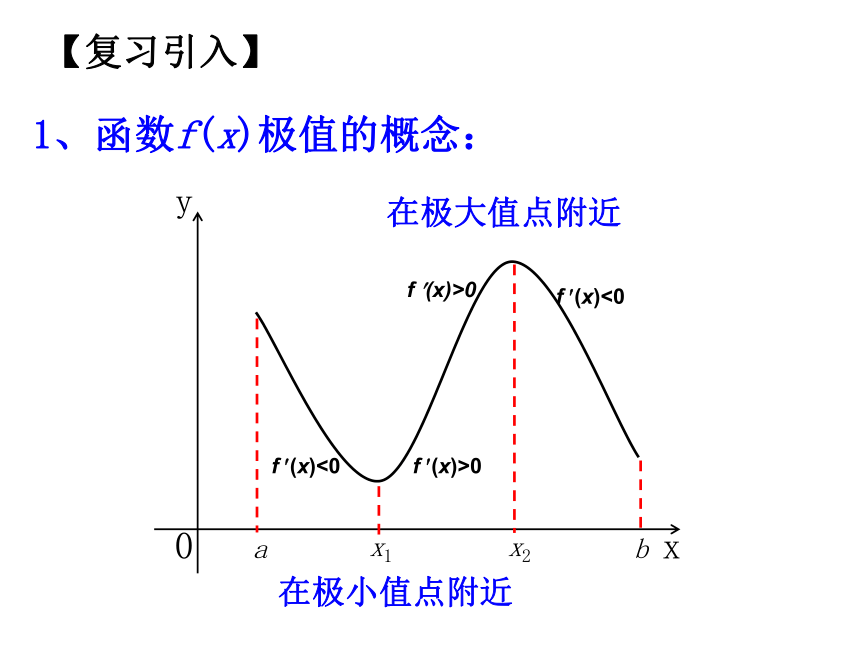
【复习引入】
f (x)<0
f (x)>0
f (x)>0
f (x)<0
在极大值点附近
0
x
y
在极小值点附近
x1
x2
a
b
1、函数f(x)极值的概念：
(1) 确定函数的定义域 ；
2、求可导函数f(x)的极值点和极值的步骤：
(2) 求出导数f (x)；
令f (x)=0，解方程； 令f (x)>0，解不等式；令f (x)<0，解不等式；
列表：用方程f (x)=0的根从小到大顺次将 定义域划分为若干个开区间，考察每个部分区间内f (x)的符号，判断f(x）的单调性从而确定极值点;
(5）结论，写出极值。
x3
x2
a
b
x1
x
O
y
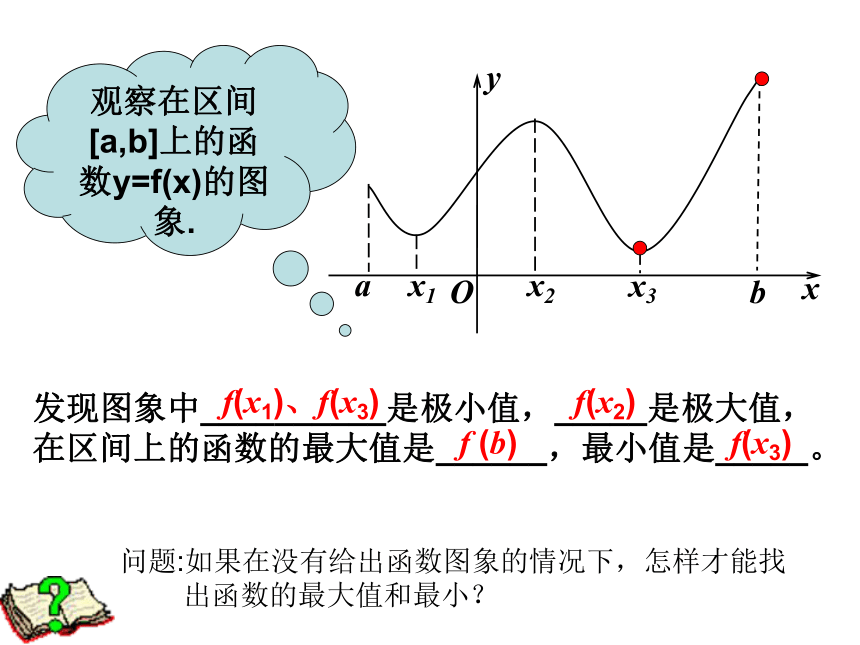
发现图象中__________是极小值，_____是极大值，在区间上的函数的最大值是______，最小值是_____。
f(x1)、f(x3)
f(x2)
f (b)
f(x3)
观察在区间[a,b]上的函数y=f(x)的图象.
问题:如果在没有给出函数图象的情况下，怎样才能找
出函数的最大值和最小？
解： =x2-4=(x-2)(x+2)
令 =0
得x=2,或x=-2
分2种情况讨论：
(1)当 >0, 即 x>2 或x<-2 ;
(2)当 <0, 即 -2当x变化时， ,f(x)的变化情况如下表；
因此，当x=2 时，f(x)有极小值，并且极小值为 f(2)=
x
f(x)
又 f(0)=4,f(3)=1
(0,2)
2
(2,3)
-
0
+
单调递减↘
单调递增↗
又x∈[0,3] ∴2又x∈[0,3] ∴0设函数f(x)在[a,b]上有定义,一般地，求函数f(x)在[a,b]上的最大值与最小值的步骤如下：
①求函数y=f(x)在(a，b)内的极值
(极大值与极小值);
②将函数y=f(x)的各极值与端点处的函数值
f(a)、f(b)作比较，其中最大的一个为最
大值，最小的一个为最小值。
练一练
注意
（1）函数的最值概念是全局性的，是对整个定义
域区间上的函数值的比较；而函数的极值是
函数的局部性质，反映的是函数在某一点附
近的大小情况。
（4）闭区间上函数的最大值（最小值）是唯一的，
而极值是可以有若干个的。
（3）函数的最大值要大于等于最小值，而函数的
极大值和极小值之间没有确定的大小关系。
（2）函数的最值可在端点处取得，也可以在极值
点处取得，但是函数的极值只能在区间内取得。
函数的最值与极值之间的区别与联系
小 结:
1、一般地，求函数f(x)在[a,b]上的最大值与最小值的步骤如下：
①求函数y=f(x)在(a，b)内的极值 (极大值与极小值);
②将函数y=f(x)的各极值与端点处的函数值f(a)、f(b)
作比较，其中最大的一个为最大值，最小的一个为
最小值。
2、函数的最值与极值间区别与联系
注意
（1）函数的最值概念是全局性的，是对整个定义
域区间上的函数值的比较；而函数的极值是
函数的局部性质，反映的是函数在某一点附
近的大小情况。
（4）闭区间上函数的最大值（最小值）是唯一的，
而极值是可以有若干个的。
（3）函数的最大值要大于等于最小值，而函数的
极大值和极小值之间没有确定的大小关系。
（2）函数的最值可在端点处取得，也可以在极值
点处取得，但是函数的极值只能在区间内取得。
函数的最值与极值之间的区别与联系
作 业
P32 习题 A、6