演绎推理
图片预览




文档简介
(共16张PPT)
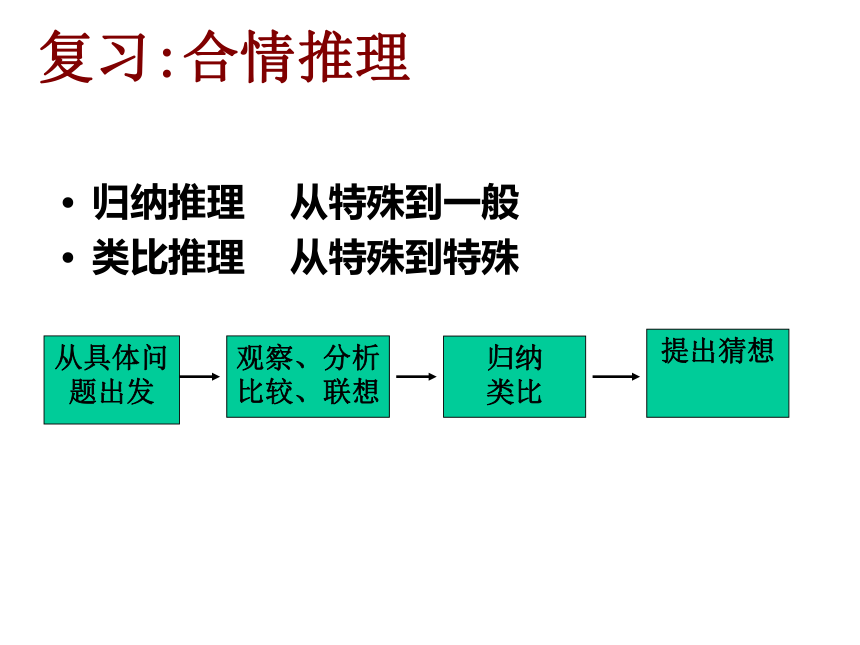
复习:合情推理
归纳推理 从特殊到一般
类比推理 从特殊到特殊
从具体问题出发
观察、分析
比较、联想
提出猜想
归纳
类比
观察与思考
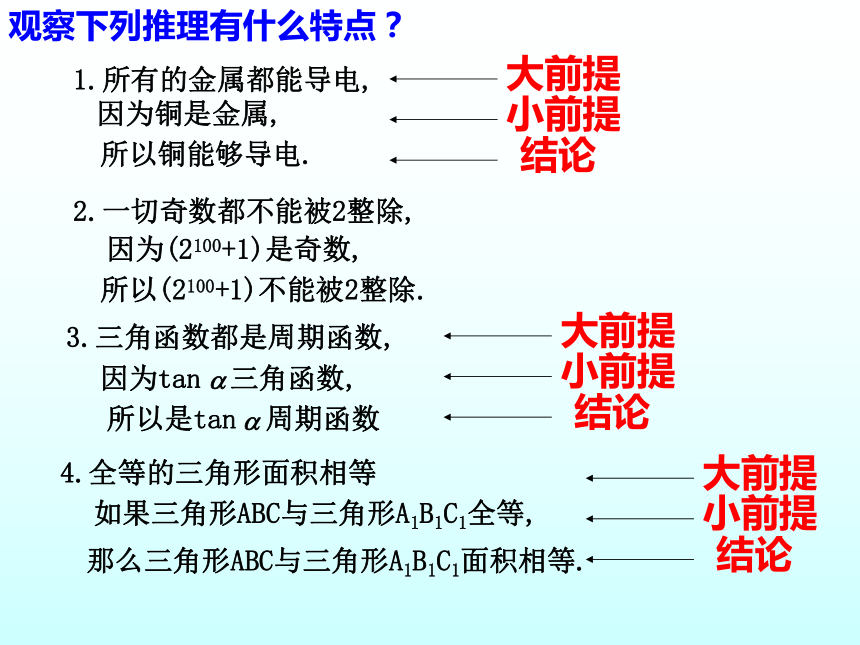
1.所有的金属都能导电,
2.一切奇数都不能被2整除,
3.三角函数都是周期函数,
铜能够导电.
铜是金属,
(2100+1)不能被2整除.
(2100+1)是奇数,
tan 周期函数
tan 三角函数,
是合情推理吗?
1.所有的金属都能导电,
2.一切奇数都不能被2整除,
3.三角函数都是周期函数,
4.全等的三角形面积相等
所以铜能够导电.
因为铜是金属,
所以(2100+1)不能被2整除.
因为(2100+1)是奇数,
因为tan 三角函数,
那么三角形ABC与三角形A1B1C1面积相等.
如果三角形ABC与三角形A1B1C1全等,
大前提
小前提
结论
大前提
小前提
结论
观察下列推理有什么特点?
所以是tan 周期函数
大前提
小前提
结论
从一般性的原理出发,推出某个特殊情况下的结论,这种推理称为演绎推理.
一、演绎推理的定义:
二、演绎推理的模式:
“三段论”是演绎推理的一般模式;
M……P(M是P)
S……M (S是M)
S……P (S是P)
大前提---已知的一般原理;
小前提---所研究的特殊对象;
结论---据一般原理,对特
殊对象做出的判断.
M
S
P
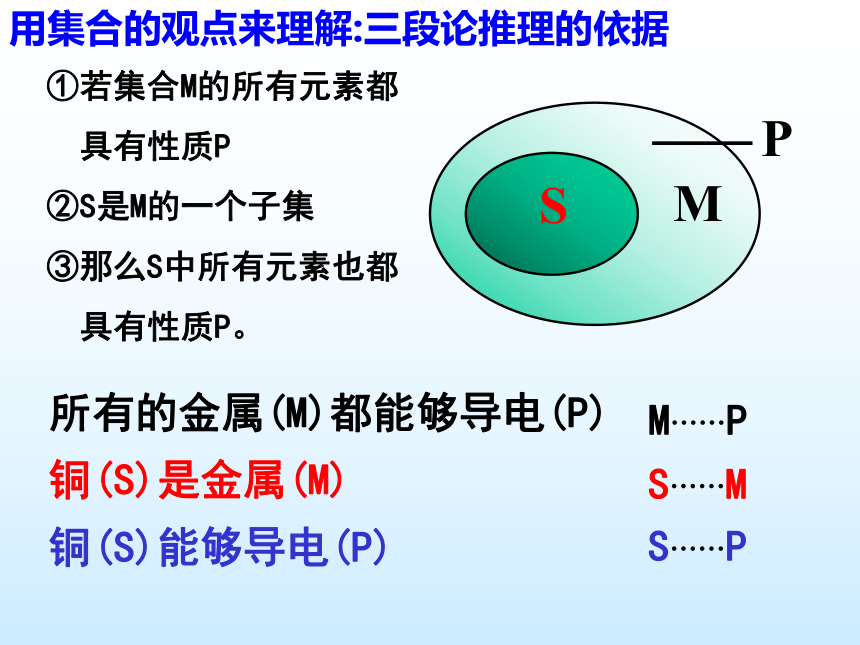
①若集合M的所有元素都
具有性质P
②S是M的一个子集
③那么S中所有元素也都
具有性质P。
所有的金属(M)都能够导电(P)
铜(S)是金属(M)
铜(S)能够导电(P)
M……P
S……M
S……P
用集合的观点来理解:三段论推理的依据
大前提
小前提
结论
所有金属都能导电 铜是金属
太阳系大行星以椭圆轨道绕太阳运行 冥王星是太阳系的大行星
奇数都不能被2整除 2007是奇数
2007不能被2整除
冥王星以椭圆形轨道绕太阳运行
铜能导电
注 演绎推理有时可用列表的形式表示,如:
例6、在锐角三角形ABC中,AD⊥BC, BE⊥AC,D,E是垂足,用演绎推理“三段论”格式证AB的中点M到D,E的距离相等.
A
D
E
C
M
B
(1)因为有一个内角是只直角的三角形是直角三角形,
在△ABC中,AD⊥BC,即∠ADB=900
所以△ABD是直角三角形
同理△ABE是直角三角形
(2)因为直角三角形斜边上的中线等于斜边的一半,
M是Rt△ABD斜边AB的中点,DM是斜边上的中线
所以 DM= AB
同理 EM= AB
所以 DM = EM
大前提
小前提
结论
大前提
小前提
结论
证明:
例7、证明函数f(x)=-x2+2x在(-∞,1]上是增函数.
满足对于任意x1,x2∈D,若x1任取x1,x2 ∈(-∞,1] 且x1f(x1)-f(x2)=(-x12+2x1)-(x22+2x2)
=(x2-x1)(x1+x2-2) 因为x10
因为x1,x2≤1所以x1+x2-2<0
因此f(x1)-f(x2)<0,即f(x1)所以函数f(x)=-x2+2x在(-∞,1]上是增函数.
大前提
小前提
结论
证明:
在证明过程中注明三段论
(1)因为指数函数 是增函数,
而 是指数函数,
所以 是增函数。
错因:大前提是错误的,所以结论是错误的。
思考:演绎推理的结论一定正确吗?
三、演绎推理的特点:
1.演绎推理的前提是一般性原理,演绎所得的的结论是蕴含于前提之中的个别、特殊事实,结论完全蕴含于前提之中,因此演绎推理是由一般到特殊的推理;
2、在演绎推理中,前提于结论之间存在着必然的联系,只要前提和推理形式是正确的,结论必定正确。因此演绎推理是数学中严格的证明工具。
3、在演绎推理是一种收敛性的思维方法,它较少创造性,但却具有条理清晰、令人信服的论证作用,有助于科学论证和系统化。
四、合情推理与演绎推理的区别
区别 推理
形式
推理结论
联系
合情推理
归纳推理
类比推理
由部分到整体、个
别到一般的推理。
由特殊到特殊
的推理。
结论不一定正确,有待进一
步证明。
演绎推理
由一般到特殊的
推理。
在大前提、小前提
和推理形式都正确
的前提下,得到的
结论一定正确。
合情推理的结论需要演绎推理的验证,而演绎
推理的方向和思路一般是通过合情推理获得的。
1、下面说法正确的有( )
(1)演绎推理是由一般到特殊的推理;
(2)演绎推理得到的结论一定是正确的;
(3)演绎推理一般模式是“三段论”形式;
(4)演绎推理的结论的正误与大前提、小前提和推理形式有关。
A、1个 B、2个 C、3个 D、4个
C
补充练习
2、用三段论的形式写出下列演绎推理。
(1)三角形内角和180°,等边三角形内
角和是180°。
(1)分析:省略了小前提:“等边三角形是三角形”。
(2) 是有理数。
(2)分析:省略了大前提:“所有的循环小数都是有理数。”
小前提: 是循环小数。
解:
三角形内角和180°,
所以等边三角形内角和是180°。
等边三角形是三角形。
3、指出下列推理中的错误,并分析产生错误的原因;
(1)整数是自然数,
-3是整数,
-3是自然数;
(2)无理数是无限小数,
是无限小数,
是无理数.
大前提 错误
演绎推理
概念
一般形式——三段论
证明问题
合情推理与演绎推理的联系与区别
(难点)
(重点)
(重点)
四、小结
复习:合情推理
归纳推理 从特殊到一般
类比推理 从特殊到特殊
从具体问题出发
观察、分析
比较、联想
提出猜想
归纳
类比
观察与思考
1.所有的金属都能导电,
2.一切奇数都不能被2整除,
3.三角函数都是周期函数,
铜能够导电.
铜是金属,
(2100+1)不能被2整除.
(2100+1)是奇数,
tan 周期函数
tan 三角函数,
是合情推理吗?
1.所有的金属都能导电,
2.一切奇数都不能被2整除,
3.三角函数都是周期函数,
4.全等的三角形面积相等
所以铜能够导电.
因为铜是金属,
所以(2100+1)不能被2整除.
因为(2100+1)是奇数,
因为tan 三角函数,
那么三角形ABC与三角形A1B1C1面积相等.
如果三角形ABC与三角形A1B1C1全等,
大前提
小前提
结论
大前提
小前提
结论
观察下列推理有什么特点?
所以是tan 周期函数
大前提
小前提
结论
从一般性的原理出发,推出某个特殊情况下的结论,这种推理称为演绎推理.
一、演绎推理的定义:
二、演绎推理的模式:
“三段论”是演绎推理的一般模式;
M……P(M是P)
S……M (S是M)
S……P (S是P)
大前提---已知的一般原理;
小前提---所研究的特殊对象;
结论---据一般原理,对特
殊对象做出的判断.
M
S
P
①若集合M的所有元素都
具有性质P
②S是M的一个子集
③那么S中所有元素也都
具有性质P。
所有的金属(M)都能够导电(P)
铜(S)是金属(M)
铜(S)能够导电(P)
M……P
S……M
S……P
用集合的观点来理解:三段论推理的依据
大前提
小前提
结论
所有金属都能导电 铜是金属
太阳系大行星以椭圆轨道绕太阳运行 冥王星是太阳系的大行星
奇数都不能被2整除 2007是奇数
2007不能被2整除
冥王星以椭圆形轨道绕太阳运行
铜能导电
注 演绎推理有时可用列表的形式表示,如:
例6、在锐角三角形ABC中,AD⊥BC, BE⊥AC,D,E是垂足,用演绎推理“三段论”格式证AB的中点M到D,E的距离相等.
A
D
E
C
M
B
(1)因为有一个内角是只直角的三角形是直角三角形,
在△ABC中,AD⊥BC,即∠ADB=900
所以△ABD是直角三角形
同理△ABE是直角三角形
(2)因为直角三角形斜边上的中线等于斜边的一半,
M是Rt△ABD斜边AB的中点,DM是斜边上的中线
所以 DM= AB
同理 EM= AB
所以 DM = EM
大前提
小前提
结论
大前提
小前提
结论
证明:
例7、证明函数f(x)=-x2+2x在(-∞,1]上是增函数.
满足对于任意x1,x2∈D,若x1
=(x2-x1)(x1+x2-2) 因为x1
因为x1,x2≤1所以x1+x2-2<0
因此f(x1)-f(x2)<0,即f(x1)
大前提
小前提
结论
证明:
在证明过程中注明三段论
(1)因为指数函数 是增函数,
而 是指数函数,
所以 是增函数。
错因:大前提是错误的,所以结论是错误的。
思考:演绎推理的结论一定正确吗?
三、演绎推理的特点:
1.演绎推理的前提是一般性原理,演绎所得的的结论是蕴含于前提之中的个别、特殊事实,结论完全蕴含于前提之中,因此演绎推理是由一般到特殊的推理;
2、在演绎推理中,前提于结论之间存在着必然的联系,只要前提和推理形式是正确的,结论必定正确。因此演绎推理是数学中严格的证明工具。
3、在演绎推理是一种收敛性的思维方法,它较少创造性,但却具有条理清晰、令人信服的论证作用,有助于科学论证和系统化。
四、合情推理与演绎推理的区别
区别 推理
形式
推理结论
联系
合情推理
归纳推理
类比推理
由部分到整体、个
别到一般的推理。
由特殊到特殊
的推理。
结论不一定正确,有待进一
步证明。
演绎推理
由一般到特殊的
推理。
在大前提、小前提
和推理形式都正确
的前提下,得到的
结论一定正确。
合情推理的结论需要演绎推理的验证,而演绎
推理的方向和思路一般是通过合情推理获得的。
1、下面说法正确的有( )
(1)演绎推理是由一般到特殊的推理;
(2)演绎推理得到的结论一定是正确的;
(3)演绎推理一般模式是“三段论”形式;
(4)演绎推理的结论的正误与大前提、小前提和推理形式有关。
A、1个 B、2个 C、3个 D、4个
C
补充练习
2、用三段论的形式写出下列演绎推理。
(1)三角形内角和180°,等边三角形内
角和是180°。
(1)分析:省略了小前提:“等边三角形是三角形”。
(2) 是有理数。
(2)分析:省略了大前提:“所有的循环小数都是有理数。”
小前提: 是循环小数。
解:
三角形内角和180°,
所以等边三角形内角和是180°。
等边三角形是三角形。
3、指出下列推理中的错误,并分析产生错误的原因;
(1)整数是自然数,
-3是整数,
-3是自然数;
(2)无理数是无限小数,
是无限小数,
是无理数.
大前提 错误
演绎推理
概念
一般形式——三段论
证明问题
合情推理与演绎推理的联系与区别
(难点)
(重点)
(重点)
四、小结
