3.1.1数系的扩充和复数的概念11
文档属性
| 名称 | 3.1.1数系的扩充和复数的概念11 |

|
|
| 格式 | zip | ||
| 文件大小 | 613.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-26 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
3.1数系的扩充和复数的概念
3.1.1数系的扩充和复数的概念
第三章
数系的扩充和复数的概念
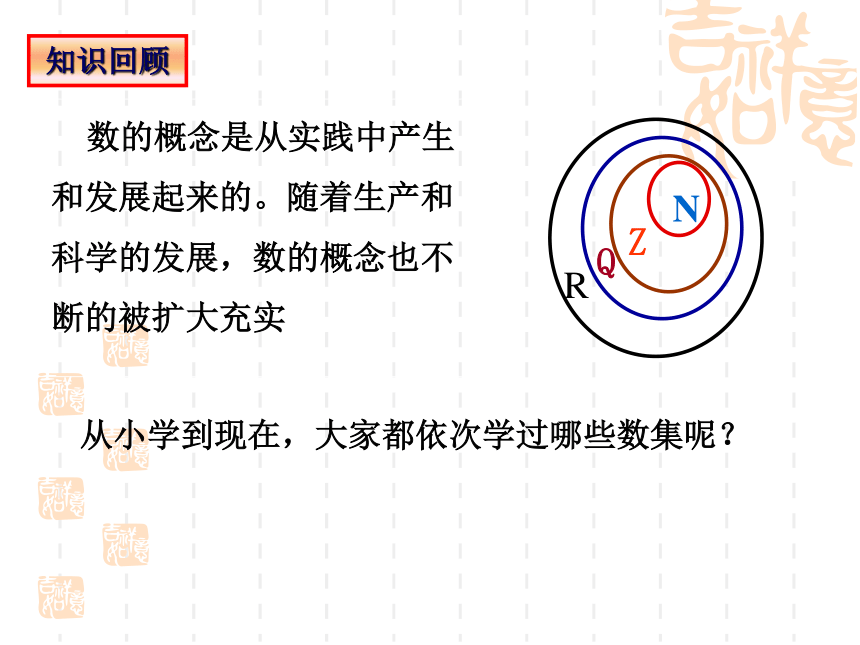
数的概念是从实践中产生和发展起来的。随着生产和科学的发展,数的概念也不断的被扩大充实
从小学到现在,大家都依次学过哪些数集呢?
知识回顾
N
Z
Q
R
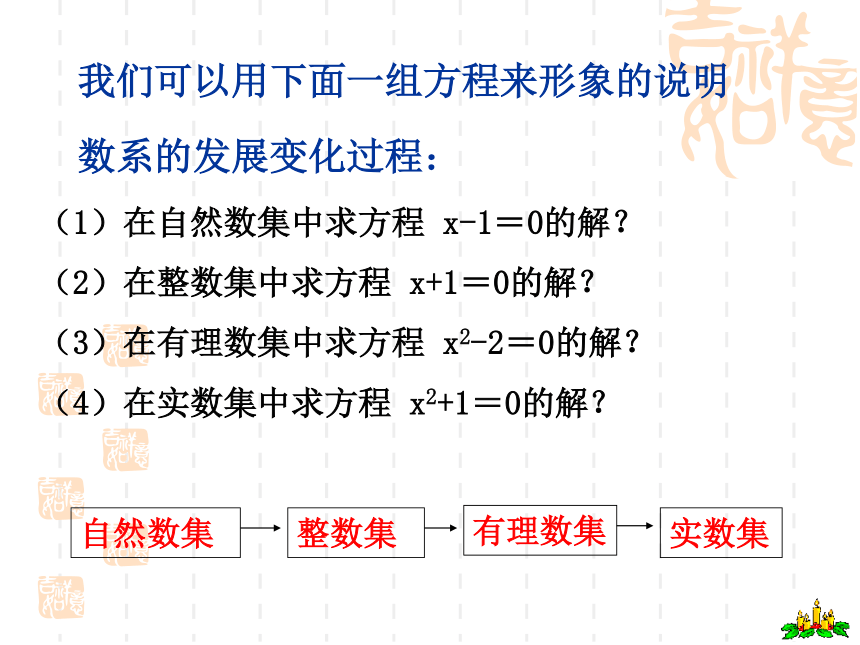
我们可以用下面一组方程来形象的说明
数系的发展变化过程:
(1)在自然数集中求方程 x-1=0的解?
(2)在整数集中求方程 x+1=0的解?
(3)在有理数集中求方程 x2-2=0的解?
(4)在实数集中求方程 x2+1=0的解?
自然数集
整数集
有理数集
实数集
知识引入
对于一元二次方程 没有实数根.
我们已经知道:
我们能否将实数集进行扩充,使得在新的数集中,该问题能得到圆满解决呢?
思考?
实际上,早在16世纪时期,数学家们就已经解决了这个矛盾,而且形成了一整套完整的理论。因为这个新数不是实数,就称为虚数单位,英文译名为imaginary number unit.所以,用“i”来表示这个新数。
引入一个新数:
引入的新数必须满足一定的条件,才能进行相关的运算,虚数单位i应满足什么条件呢?
新课讲解
引入一个数 i ,规定:
(1)它的平方等于-1 即i 2 1;
(2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算律(包括交换律、结合律和分配律)仍然成立。
由上述规定出现了
形如a+bi(a,b∈R)的数.
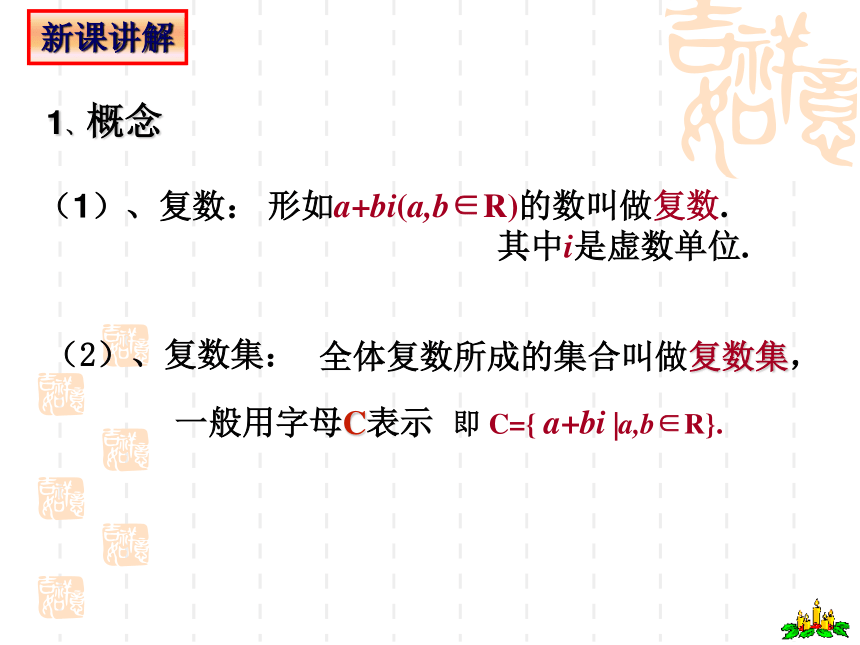
(1)、复数:
(2)、复数集:
新课讲解
1、概念
形如a+bi(a,b∈R)的数叫做复数.
其中i是虚数单位.
全体复数所成的集合叫做复数集,
一般用字母C表示
即 C={ a+bi |a,b∈R}.
实部
2、复数的代数形式:
通常用字母 z 表示,即
虚部
其中 称为虚数单位。
讲解新课
说出下列复数的实部和虚部
练一练
Z=0 + 0 i
复数集C和实数集R之间有什么关系?
讨论?
3.复数的分类:
í
ì
í
ì
0
0
b
a
且
非纯虚数
=
0
0
b
a
且
纯虚数
0
b
虚数
=
0
b
实数
虚数集
复数集
实数集
纯虚数集
4.规定:如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
注:
2) 一般来说,两个不全为实数的复数只能说相等或不相等,而不能比较大小.
1.说明下列数中,那些是实数,哪些是虚数,哪些是纯虚数.
0
0,
实数:
虚数:
纯虚数:
2、判断下列命题是否正确:
(1)若a、b为实数,则z=a+bi为虚数
(2)若b为实数,则z=bi必为纯虚数
(3)若a为实数,则z= a一定不是虚数
×
×
√
若b=0则
z为实数
若z=bi为纯虚数则
例1.实数 m 取什么数值时,复数z=m +1+(m-1)i是:
(1)实数? (2)虚数?(3)纯虚数?
解:复数z=m+1+(m-1)i 中,因为m∈R,所以m+1,m-1都是实数,它们分别是z的实部和虚部,
∴(1) 当m-1 =0,即m=1时,复数z是实数;
(2) 当m-1 ≠0,即 m≠1时,复数z是虚数;
(3)当 时,即m=-1时,z是纯虚数;
练习:当m为何实数时,复数
是(1)实数 (2)虚数 (3)纯虚数
例2.已知(2x-1)+i=y-(3-y)i,其中x, y∈R,求x, y值.
解:根据复数相等的意义,两个复数相等则实部等于实部 ,虚部等于虚部,得方程组,
解得 x= , y =4.
1.对于实数m,指出复数z的实部和虚部;
2.实数m为何值时,
(1)实数?
(2)虚数?
(3)零?
(4)纯虚数?
(5)负数?
知识拓展
3.1数系的扩充和复数的概念
3.1.1数系的扩充和复数的概念
第三章
数系的扩充和复数的概念
数的概念是从实践中产生和发展起来的。随着生产和科学的发展,数的概念也不断的被扩大充实
从小学到现在,大家都依次学过哪些数集呢?
知识回顾
N
Z
Q
R
我们可以用下面一组方程来形象的说明
数系的发展变化过程:
(1)在自然数集中求方程 x-1=0的解?
(2)在整数集中求方程 x+1=0的解?
(3)在有理数集中求方程 x2-2=0的解?
(4)在实数集中求方程 x2+1=0的解?
自然数集
整数集
有理数集
实数集
知识引入
对于一元二次方程 没有实数根.
我们已经知道:
我们能否将实数集进行扩充,使得在新的数集中,该问题能得到圆满解决呢?
思考?
实际上,早在16世纪时期,数学家们就已经解决了这个矛盾,而且形成了一整套完整的理论。因为这个新数不是实数,就称为虚数单位,英文译名为imaginary number unit.所以,用“i”来表示这个新数。
引入一个新数:
引入的新数必须满足一定的条件,才能进行相关的运算,虚数单位i应满足什么条件呢?
新课讲解
引入一个数 i ,规定:
(1)它的平方等于-1 即i 2 1;
(2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算律(包括交换律、结合律和分配律)仍然成立。
由上述规定出现了
形如a+bi(a,b∈R)的数.
(1)、复数:
(2)、复数集:
新课讲解
1、概念
形如a+bi(a,b∈R)的数叫做复数.
其中i是虚数单位.
全体复数所成的集合叫做复数集,
一般用字母C表示
即 C={ a+bi |a,b∈R}.
实部
2、复数的代数形式:
通常用字母 z 表示,即
虚部
其中 称为虚数单位。
讲解新课
说出下列复数的实部和虚部
练一练
Z=0 + 0 i
复数集C和实数集R之间有什么关系?
讨论?
3.复数的分类:
í
ì
í
ì
0
0
b
a
且
非纯虚数
=
0
0
b
a
且
纯虚数
0
b
虚数
=
0
b
实数
虚数集
复数集
实数集
纯虚数集
4.规定:如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
注:
2) 一般来说,两个不全为实数的复数只能说相等或不相等,而不能比较大小.
1.说明下列数中,那些是实数,哪些是虚数,哪些是纯虚数.
0
0,
实数:
虚数:
纯虚数:
2、判断下列命题是否正确:
(1)若a、b为实数,则z=a+bi为虚数
(2)若b为实数,则z=bi必为纯虚数
(3)若a为实数,则z= a一定不是虚数
×
×
√
若b=0则
z为实数
若z=bi为纯虚数则
例1.实数 m 取什么数值时,复数z=m +1+(m-1)i是:
(1)实数? (2)虚数?(3)纯虚数?
解:复数z=m+1+(m-1)i 中,因为m∈R,所以m+1,m-1都是实数,它们分别是z的实部和虚部,
∴(1) 当m-1 =0,即m=1时,复数z是实数;
(2) 当m-1 ≠0,即 m≠1时,复数z是虚数;
(3)当 时,即m=-1时,z是纯虚数;
练习:当m为何实数时,复数
是(1)实数 (2)虚数 (3)纯虚数
例2.已知(2x-1)+i=y-(3-y)i,其中x, y∈R,求x, y值.
解:根据复数相等的意义,两个复数相等则实部等于实部 ,虚部等于虚部,得方程组,
解得 x= , y =4.
1.对于实数m,指出复数z的实部和虚部;
2.实数m为何值时,
(1)实数?
(2)虚数?
(3)零?
(4)纯虚数?
(5)负数?
知识拓展
