高中数学回归分析_课件苏教版选修1-2
文档属性
| 名称 | 高中数学回归分析_课件苏教版选修1-2 |

|
|
| 格式 | zip | ||
| 文件大小 | 316.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-26 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
回归分析
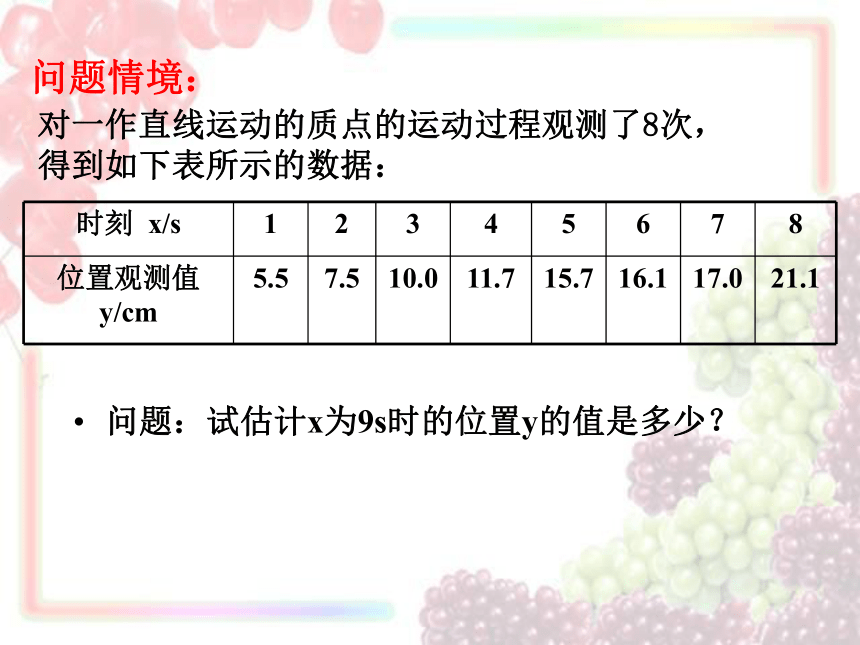
对一作直线运动的质点的运动过程观测了8次,得到如下表所示的数据:
问题情境:
时刻 x/s 1 2 3 4 5 6 7 8
位置观测值 y/cm 5.5 7.5 10.0 11.7 15.7 16.1 17.0 21.1
问题:试估计x为9s时的位置y的值是多少?
0
2
4
6
8
10
5
10
15
20
25
●
●
●
●
●
●
●
●
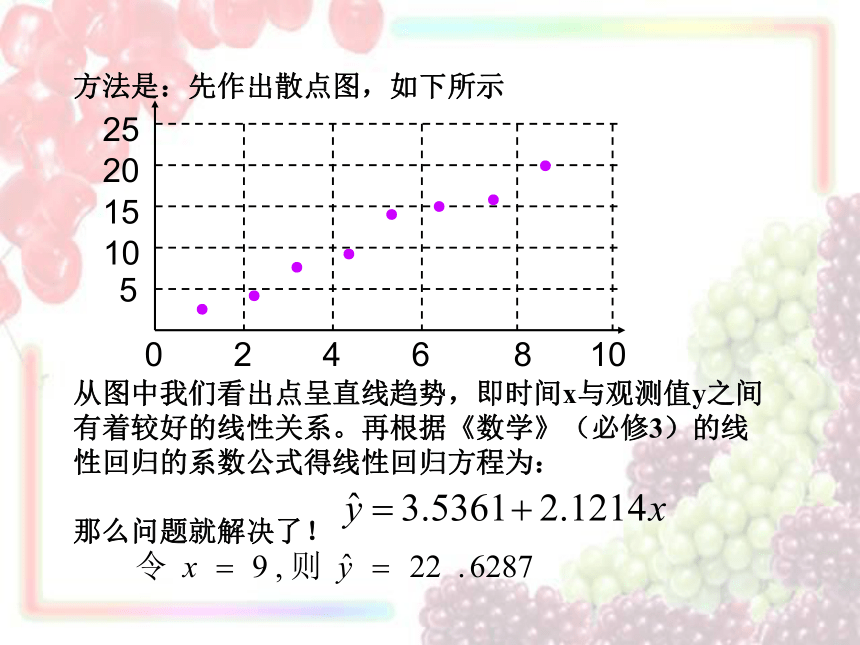
方法是:先作出散点图,如下所示
从图中我们看出点呈直线趋势,即时间x与观测值y之间有着较好的线性关系。再根据《数学》(必修3)的线性回归的系数公式得线性回归方程为:
那么问题就解决了!
学生活动:
这个结果是否一定很准确?为什么?
结果不准确,而是存在一些误差,其原因有:①所用的确定型函数不恰当②忽略了某些因素的影响③存在观测误差
注:两个相互联系的变量之间的关系大体有两种:一是确定性函数关系,另一个是非确定性关系(如相关关系)
建构数学:
用
表示上述两个变量x与y关系,也称为线性回归模型。
其中
是确定性函数关系, 表示随机误差 。
对于一个问题来说,如果用
这样的模型表示两个变量的关系,那么
(1)这个模型合理吗?
(2)如果模型合理,又如何求出其中的a与b的值?
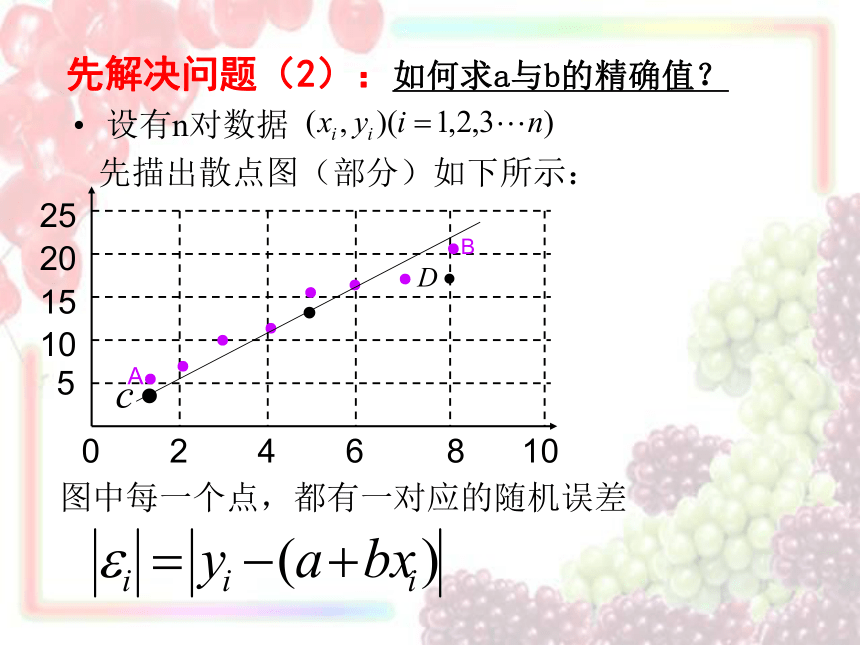
先解决问题(2):如何求a与b的精确值?
设有n对数据
先描出散点图(部分)如下所示:
0
2
4
6
8
10
5
10
15
20
25
A●
●
●
●
●
●
●
●B
图中每一个点,都有一对应的随机误差
我们希望总误差最小,即下式值最小
而此时求出的a与b值可作为较精确的值,
通常记为
计算公式为:
(1)
此处为最小二乘法(见《数学》必修3)
也可以化为
称为线性回归方程,对应的直线为回归直线, 为回归截距, 为回归系数, 为回归值。
数学应用1:
例1:下表给出了我国从1949年到1999年的人口数据资料,根据表中数据估计我国2004年的人口数。
年份(x) 1949 1954 1959 1964 1969 1974 1979 1984 1989 1994 1999
人口数/百万(y) 542 603 672 705 807 909 975 1035 1107 1177 1246
求回归方程步骤:
(1)作散点图(有样本点是否呈直线趋势来判断两个变量是否线性相关)
(2)根据公式求回归系数 和回归截距
(3)写出回归方程,根据需要进行预测估计
简解:作出散点图发现点在一条直线附近,可以用
来表示变量x与y关系,根据公式(1)算得
则线性回归方程为
从而估计出2004年的人口数。
再解决问题(1):检验模型是否合理?
对随机抽取的n对数据
样本相关系数r的计算公式为
(2)
称为对两个变量的相关性检验
相关系数r的性质:
(1)
(2) 越接近于1,x与y的线性相关
程度越强;
(3) 越接近于0,x与y的线性相关程度越弱;
对r进行显著性检验,步骤如下:
(1)提出统计假设 :变量x, y不具有线性
相关关系
(2)如果以95%的把握做判断,通过课本93页的附录1查出一个r的临界值
(其中1-0.95=0.05称为检验水平)
(3)计算样本相关系数r
(4)做出统计判断:
若 则否定假设 ,表明有95%的
把握认为变量x, y之间具有线性相关关系;
若 则不拒绝假设,即没有充分理由
认为变量x, y具有线性相关关系
对于刚才讲的例题1,可以这样检验:
(1)提出统计假设 :变量x, y不具有线性相关关系
(2)由0.05与 在课本93页查得
(3)根据公式(2)计算得线性相关系数为r =0.998
(4)因为|r| =0.998>0.602,所以有95%的把握认为变量
x, y具有线性相关关系,即所求出的线性方程是有意义的
例2:随机抽取8对母女的身高数据,试根据这些数据探讨y与x之间的关系。
母亲身高x/cm 154 157 158 159 160 161 162 163
女儿身高y/cm 155 156 159 162 161 164 165 166
数学应用2:
简解:作出散点图发现点在一条直线附近,
∵
几个值都可以算出来(通过计算器计算)
∴
又∵
∴认为x与y具有线性关系
又由公式(1)得
则回归方程为
提醒:
在用公式(2)计算样本相关系数r时,需要根据
公式特点先求出
回顾反思:
1.判断两个变量是否具有线性相关关系,可以通过散点图或者进行相关性检验判断。
2.对具有线性关系的两个变量,他们的回归方程通过公式(1)来求出,方程到底是否有意义还需要进行相关性检验(用到公式(2))来判断。
回归分析
对一作直线运动的质点的运动过程观测了8次,得到如下表所示的数据:
问题情境:
时刻 x/s 1 2 3 4 5 6 7 8
位置观测值 y/cm 5.5 7.5 10.0 11.7 15.7 16.1 17.0 21.1
问题:试估计x为9s时的位置y的值是多少?
0
2
4
6
8
10
5
10
15
20
25
●
●
●
●
●
●
●
●
方法是:先作出散点图,如下所示
从图中我们看出点呈直线趋势,即时间x与观测值y之间有着较好的线性关系。再根据《数学》(必修3)的线性回归的系数公式得线性回归方程为:
那么问题就解决了!
学生活动:
这个结果是否一定很准确?为什么?
结果不准确,而是存在一些误差,其原因有:①所用的确定型函数不恰当②忽略了某些因素的影响③存在观测误差
注:两个相互联系的变量之间的关系大体有两种:一是确定性函数关系,另一个是非确定性关系(如相关关系)
建构数学:
用
表示上述两个变量x与y关系,也称为线性回归模型。
其中
是确定性函数关系, 表示随机误差 。
对于一个问题来说,如果用
这样的模型表示两个变量的关系,那么
(1)这个模型合理吗?
(2)如果模型合理,又如何求出其中的a与b的值?
先解决问题(2):如何求a与b的精确值?
设有n对数据
先描出散点图(部分)如下所示:
0
2
4
6
8
10
5
10
15
20
25
A●
●
●
●
●
●
●
●B
图中每一个点,都有一对应的随机误差
我们希望总误差最小,即下式值最小
而此时求出的a与b值可作为较精确的值,
通常记为
计算公式为:
(1)
此处为最小二乘法(见《数学》必修3)
也可以化为
称为线性回归方程,对应的直线为回归直线, 为回归截距, 为回归系数, 为回归值。
数学应用1:
例1:下表给出了我国从1949年到1999年的人口数据资料,根据表中数据估计我国2004年的人口数。
年份(x) 1949 1954 1959 1964 1969 1974 1979 1984 1989 1994 1999
人口数/百万(y) 542 603 672 705 807 909 975 1035 1107 1177 1246
求回归方程步骤:
(1)作散点图(有样本点是否呈直线趋势来判断两个变量是否线性相关)
(2)根据公式求回归系数 和回归截距
(3)写出回归方程,根据需要进行预测估计
简解:作出散点图发现点在一条直线附近,可以用
来表示变量x与y关系,根据公式(1)算得
则线性回归方程为
从而估计出2004年的人口数。
再解决问题(1):检验模型是否合理?
对随机抽取的n对数据
样本相关系数r的计算公式为
(2)
称为对两个变量的相关性检验
相关系数r的性质:
(1)
(2) 越接近于1,x与y的线性相关
程度越强;
(3) 越接近于0,x与y的线性相关程度越弱;
对r进行显著性检验,步骤如下:
(1)提出统计假设 :变量x, y不具有线性
相关关系
(2)如果以95%的把握做判断,通过课本93页的附录1查出一个r的临界值
(其中1-0.95=0.05称为检验水平)
(3)计算样本相关系数r
(4)做出统计判断:
若 则否定假设 ,表明有95%的
把握认为变量x, y之间具有线性相关关系;
若 则不拒绝假设,即没有充分理由
认为变量x, y具有线性相关关系
对于刚才讲的例题1,可以这样检验:
(1)提出统计假设 :变量x, y不具有线性相关关系
(2)由0.05与 在课本93页查得
(3)根据公式(2)计算得线性相关系数为r =0.998
(4)因为|r| =0.998>0.602,所以有95%的把握认为变量
x, y具有线性相关关系,即所求出的线性方程是有意义的
例2:随机抽取8对母女的身高数据,试根据这些数据探讨y与x之间的关系。
母亲身高x/cm 154 157 158 159 160 161 162 163
女儿身高y/cm 155 156 159 162 161 164 165 166
数学应用2:
简解:作出散点图发现点在一条直线附近,
∵
几个值都可以算出来(通过计算器计算)
∴
又∵
∴认为x与y具有线性关系
又由公式(1)得
则回归方程为
提醒:
在用公式(2)计算样本相关系数r时,需要根据
公式特点先求出
回顾反思:
1.判断两个变量是否具有线性相关关系,可以通过散点图或者进行相关性检验判断。
2.对具有线性关系的两个变量,他们的回归方程通过公式(1)来求出,方程到底是否有意义还需要进行相关性检验(用到公式(2))来判断。
