双曲线的简单性质
图片预览




文档简介
(共16张PPT)
双曲线的简单性质(1)
双曲线的标准方程的推导:
双曲线的标准方程:
(焦点在x轴上)
(焦点在y轴上)
其中
x
y
x
y
o
o
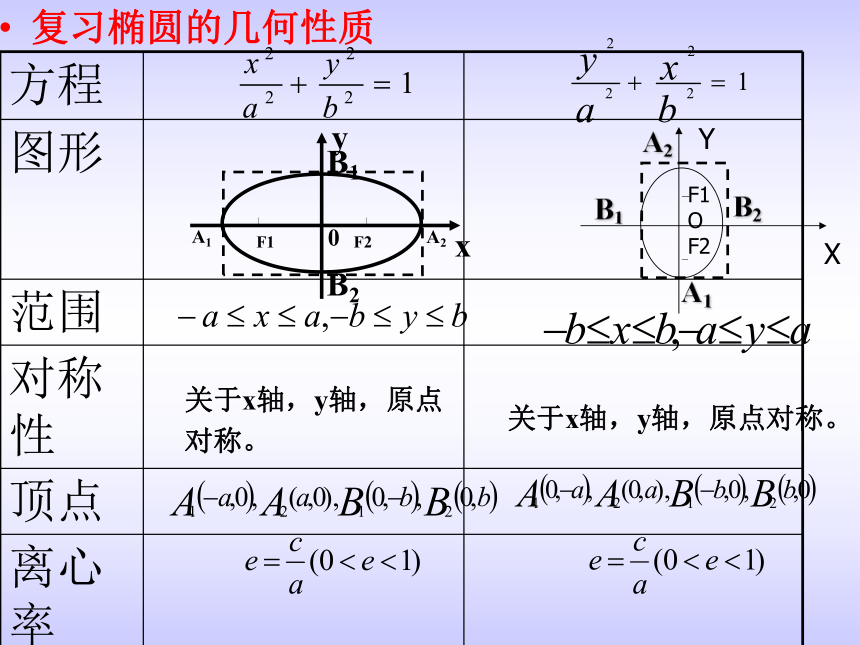
方程
图形
范围
对称性
顶点
离心率
x
y
B1
B2
A1
A2
∣ ∣
F1 F2
Y
X
F1
O
F2
_
_
A2
A1
B1
B2
0
关于x轴,y轴,原点
对称。
关于x轴,y轴,原点对称。
复习椭圆的几何性质
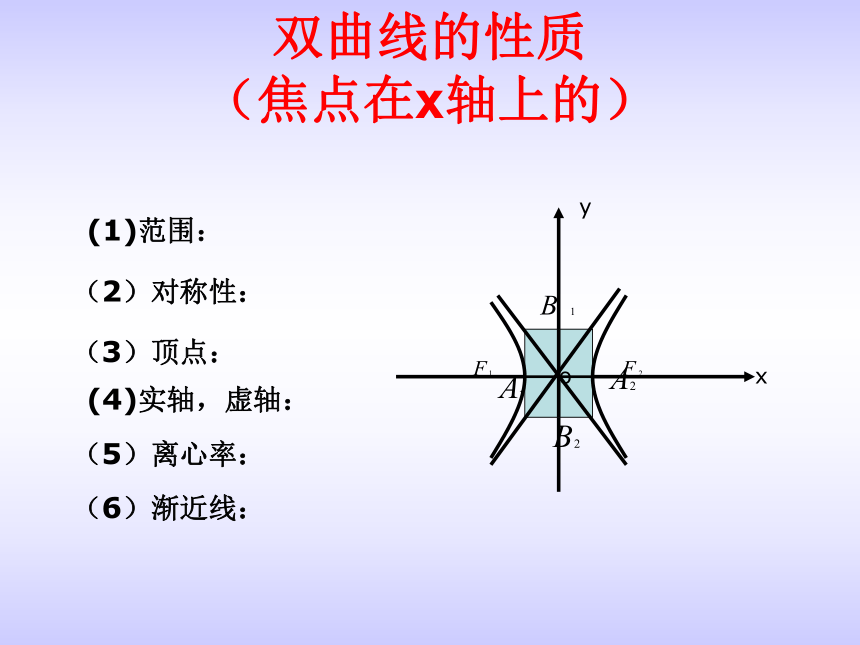
双曲线的性质
(焦点在x轴上的)
x
y
o
(1)范围:
(2)对称性:
(3)顶点:
(4)实轴,虚轴:
(5)离心率:
(6)渐近线:
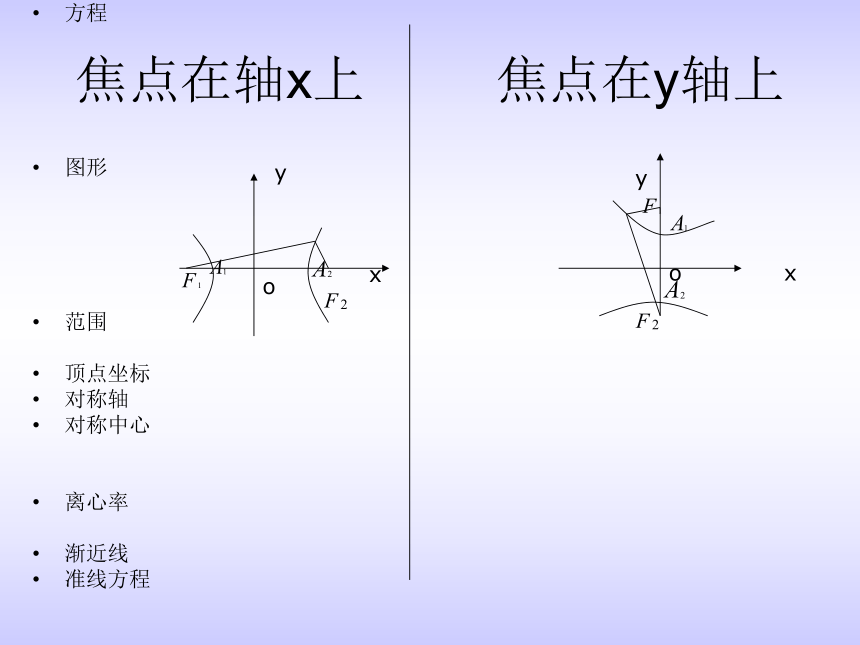
焦点在轴x上 焦点在y轴上
方程
图形
范围
顶点坐标
对称轴
对称中心
离心率
渐近线
准线方程
x
y
o
x
y
o
顶点坐标(-a,0) (a,0) (0,a) (0,-a)
对称轴:x=0,y=0
对称中心 (0,0)
离心率
渐近线
准线方程
例1:求双曲线 的实半轴长虚半轴长,焦点坐标,离心率,渐近线方程。
解:把方程化为标准方程
由此可知,实半轴长a=4,虚半轴长b=3.
C=5
焦点的坐标是(0,5)(0,-5)
离心率e=
渐近线方程为
1 求下列双曲线的实轴和虚轴的长,顶点和焦点坐标,离心率,渐近线方程。
(1)
(2)
(3)
(4)
当渐近线的方程为 时,
双曲线的标准方程一定是
吗?
如果不是,举出一个反例。
2 提出问题
答:不一定是。
例2 双曲线型自然通风塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面,它的最小半径为12m,上口半径为13m,下口半径为25m,高55m.选择适当的坐标系,求出此双曲线的方程(精确到1m)
x
y
o
A
B
C
13
12
25
(13,y)
(25,y-55)
例3:点M(x,y)与定点F(C,0)的距离和它到定直线L: 的距离的比是常数 (c>a>0) ,求点M的轨迹。
F
F
0
x
y
M
L
(c,0)
解:设d是点M到直线L的距离。
双曲线的第二定义:
平面内的点到一个定点的距离和它到定直线的距离的比,是一个大于1的常数e的点的轨迹,是双曲线。其中定点是双曲线的焦点,定直线叫做双曲线的准线,常数e是双曲线的离心率。
M
练习1:求以椭圆 的焦点为顶点,而以椭圆的顶点为焦点的双曲线方程。
解:椭圆的焦点为F( )F,( ),顶点为( )( )( )( )双曲线是是以F,F,为顶点,以 , 为
焦点的双曲线。
X
Y
练习2:等轴双曲线的一个焦点是(-6,0),求它的标准方程和渐近线方程。
解:
渐近线方程:
练习1:双曲线虚轴的一个端点为M,两个焦点
,则双曲线的离心率为多少?
练习2:求中心在原点,对称轴为坐标轴,经过点P(1,3)且离心率为 的双曲线标准方程。
练习3:已知点A(3,2),F(2,0),在双曲线 上求一点P,使 的值最小。
练习4 :已知双曲线的渐近线方程为 两条准线间
的距离为 ,求双曲线的标准方程。
双曲线的简单性质(1)
双曲线的标准方程的推导:
双曲线的标准方程:
(焦点在x轴上)
(焦点在y轴上)
其中
x
y
x
y
o
o
方程
图形
范围
对称性
顶点
离心率
x
y
B1
B2
A1
A2
∣ ∣
F1 F2
Y
X
F1
O
F2
_
_
A2
A1
B1
B2
0
关于x轴,y轴,原点
对称。
关于x轴,y轴,原点对称。
复习椭圆的几何性质
双曲线的性质
(焦点在x轴上的)
x
y
o
(1)范围:
(2)对称性:
(3)顶点:
(4)实轴,虚轴:
(5)离心率:
(6)渐近线:
焦点在轴x上 焦点在y轴上
方程
图形
范围
顶点坐标
对称轴
对称中心
离心率
渐近线
准线方程
x
y
o
x
y
o
顶点坐标(-a,0) (a,0) (0,a) (0,-a)
对称轴:x=0,y=0
对称中心 (0,0)
离心率
渐近线
准线方程
例1:求双曲线 的实半轴长虚半轴长,焦点坐标,离心率,渐近线方程。
解:把方程化为标准方程
由此可知,实半轴长a=4,虚半轴长b=3.
C=5
焦点的坐标是(0,5)(0,-5)
离心率e=
渐近线方程为
1 求下列双曲线的实轴和虚轴的长,顶点和焦点坐标,离心率,渐近线方程。
(1)
(2)
(3)
(4)
当渐近线的方程为 时,
双曲线的标准方程一定是
吗?
如果不是,举出一个反例。
2 提出问题
答:不一定是。
例2 双曲线型自然通风塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面,它的最小半径为12m,上口半径为13m,下口半径为25m,高55m.选择适当的坐标系,求出此双曲线的方程(精确到1m)
x
y
o
A
B
C
13
12
25
(13,y)
(25,y-55)
例3:点M(x,y)与定点F(C,0)的距离和它到定直线L: 的距离的比是常数 (c>a>0) ,求点M的轨迹。
F
F
0
x
y
M
L
(c,0)
解:设d是点M到直线L的距离。
双曲线的第二定义:
平面内的点到一个定点的距离和它到定直线的距离的比,是一个大于1的常数e的点的轨迹,是双曲线。其中定点是双曲线的焦点,定直线叫做双曲线的准线,常数e是双曲线的离心率。
M
练习1:求以椭圆 的焦点为顶点,而以椭圆的顶点为焦点的双曲线方程。
解:椭圆的焦点为F( )F,( ),顶点为( )( )( )( )双曲线是是以F,F,为顶点,以 , 为
焦点的双曲线。
X
Y
练习2:等轴双曲线的一个焦点是(-6,0),求它的标准方程和渐近线方程。
解:
渐近线方程:
练习1:双曲线虚轴的一个端点为M,两个焦点
,则双曲线的离心率为多少?
练习2:求中心在原点,对称轴为坐标轴,经过点P(1,3)且离心率为 的双曲线标准方程。
练习3:已知点A(3,2),F(2,0),在双曲线 上求一点P,使 的值最小。
练习4 :已知双曲线的渐近线方程为 两条准线间
的距离为 ,求双曲线的标准方程。
