直线与双曲线的位置关系
图片预览



文档简介
(共15张PPT)
直线与双曲线的位置关系
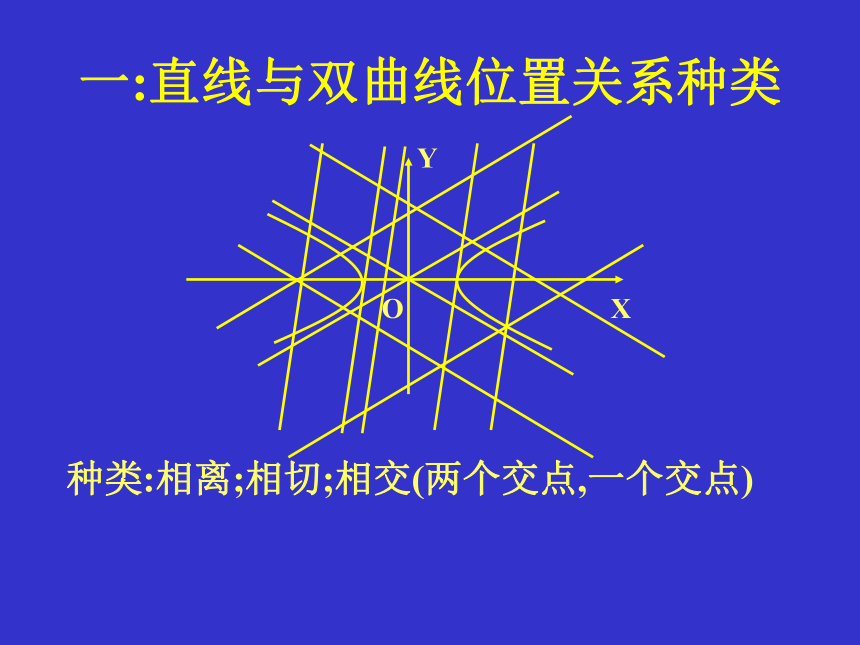
一:直线与双曲线位置关系种类
X
Y
O
种类:相离;相切;相交(两个交点,一个交点)
X
Y
O
X
Y
O
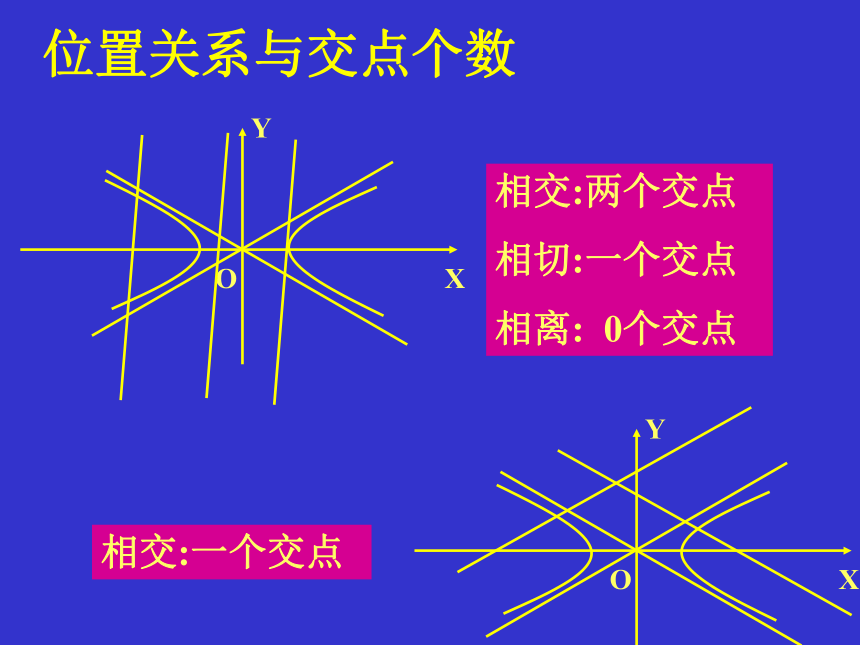
相交:两个交点
相切:一个交点
相离: 0个交点
相交:一个交点
位置关系与交点个数
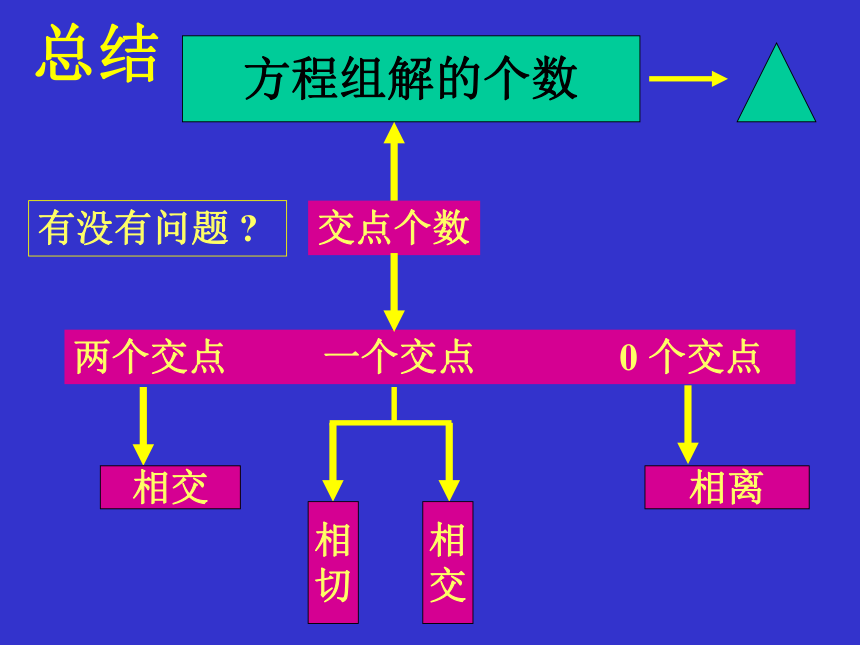
总结
两个交点 一个交点 0 个交点
相交
相
切
相
交
相离
交点个数
方程组解的个数
有没有问题
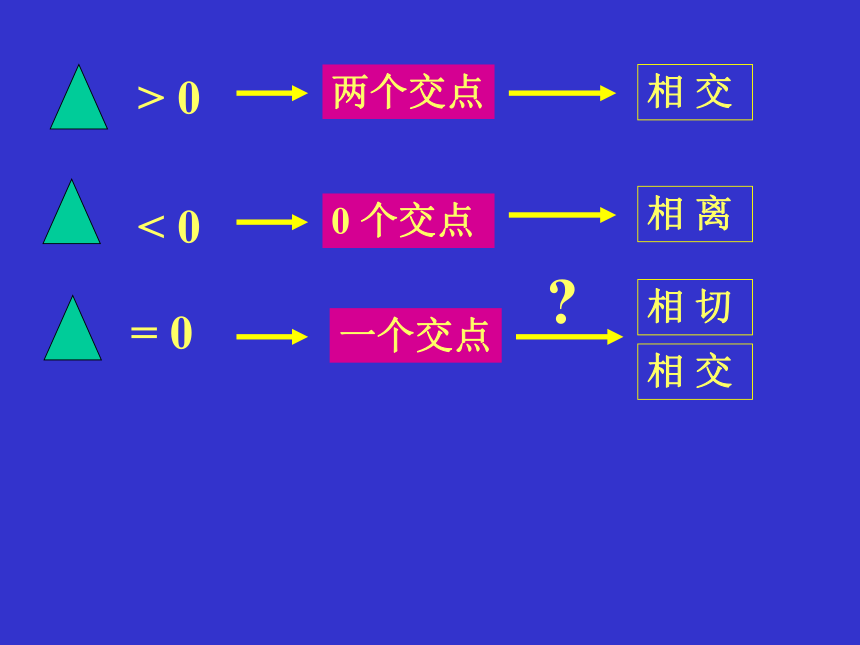
= 0
一个交点
相 切
相 交
> 0
< 0
0 个交点
两个交点
相 离
相 交
[1] 0 个交点和两个交点的情况都正常,
那么 ,依然可以用判别式判断位置关系
[2]一个交点却包括了两种位置关系:
相切和相交 ( 特殊的相交 ) , 那么是否意味着判别式等于零时 , 即可能相切也可能相交
实践是检验真理的唯一标准 !
请判断下列直线与双曲线之间的位置关系
[1]
[2]
相 切
相 交
回顾一下:判别式情况如何
一般情况的研究
显然,这条直线与双曲线的渐进线是平行的,也就是相交.把直线方程代入双曲线方程,看看判别式如何
根本就没有判别式 !
当直线与双曲线的渐进线平行时 , 把直线方程代入双曲线方程 , 得到的是一次方程 , 根本得不到一元二次方程 , 当然也就没有所谓的判别式了 。
结论:判别式依然可以判断直线与双曲线的位置关系 !
判断直线与双曲线位置关系的操作程序
把直线方程代入双曲线方程
得到一元一次方程
得到一元二次方程
直线与双曲线的
渐进线平行
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
判断下列直线与双曲线的位置关系
相交(一个交点)
相离
例题: 如果直线y=kx-1与双曲线x2-y2=4
没有公共点,求k的取值范围。
分析:因为直线与双曲线没有交点,所以它们方程组成的方程组无解,即消去一个未知数后得到的一元二次方程的判别式△<0
即此方程无解
变式一: 如果直线y=kx-1与双曲线x2-y2=4
有两个公共点,求k的取值范围。
变式二: 如果直线y=kx-1与双曲线x2-y2=4
有一个公共点,求k的值。
直线与双曲线的位置关系
一:直线与双曲线位置关系种类
X
Y
O
种类:相离;相切;相交(两个交点,一个交点)
X
Y
O
X
Y
O
相交:两个交点
相切:一个交点
相离: 0个交点
相交:一个交点
位置关系与交点个数
总结
两个交点 一个交点 0 个交点
相交
相
切
相
交
相离
交点个数
方程组解的个数
有没有问题
= 0
一个交点
相 切
相 交
> 0
< 0
0 个交点
两个交点
相 离
相 交
[1] 0 个交点和两个交点的情况都正常,
那么 ,依然可以用判别式判断位置关系
[2]一个交点却包括了两种位置关系:
相切和相交 ( 特殊的相交 ) , 那么是否意味着判别式等于零时 , 即可能相切也可能相交
实践是检验真理的唯一标准 !
请判断下列直线与双曲线之间的位置关系
[1]
[2]
相 切
相 交
回顾一下:判别式情况如何
一般情况的研究
显然,这条直线与双曲线的渐进线是平行的,也就是相交.把直线方程代入双曲线方程,看看判别式如何
根本就没有判别式 !
当直线与双曲线的渐进线平行时 , 把直线方程代入双曲线方程 , 得到的是一次方程 , 根本得不到一元二次方程 , 当然也就没有所谓的判别式了 。
结论:判别式依然可以判断直线与双曲线的位置关系 !
判断直线与双曲线位置关系的操作程序
把直线方程代入双曲线方程
得到一元一次方程
得到一元二次方程
直线与双曲线的
渐进线平行
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
判断下列直线与双曲线的位置关系
相交(一个交点)
相离
例题: 如果直线y=kx-1与双曲线x2-y2=4
没有公共点,求k的取值范围。
分析:因为直线与双曲线没有交点,所以它们方程组成的方程组无解,即消去一个未知数后得到的一元二次方程的判别式△<0
即此方程无解
变式一: 如果直线y=kx-1与双曲线x2-y2=4
有两个公共点,求k的取值范围。
变式二: 如果直线y=kx-1与双曲线x2-y2=4
有一个公共点,求k的值。
