高中数学 1.3.1空间几何体的表面积课件 新人教A版必修2
文档属性
| 名称 | 高中数学 1.3.1空间几何体的表面积课件 新人教A版必修2 |

|
|
| 格式 | zip | ||
| 文件大小 | 268.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-26 00:00:00 | ||
图片预览

文档简介
(共22张PPT)
1.3.1空间几何体的表面积
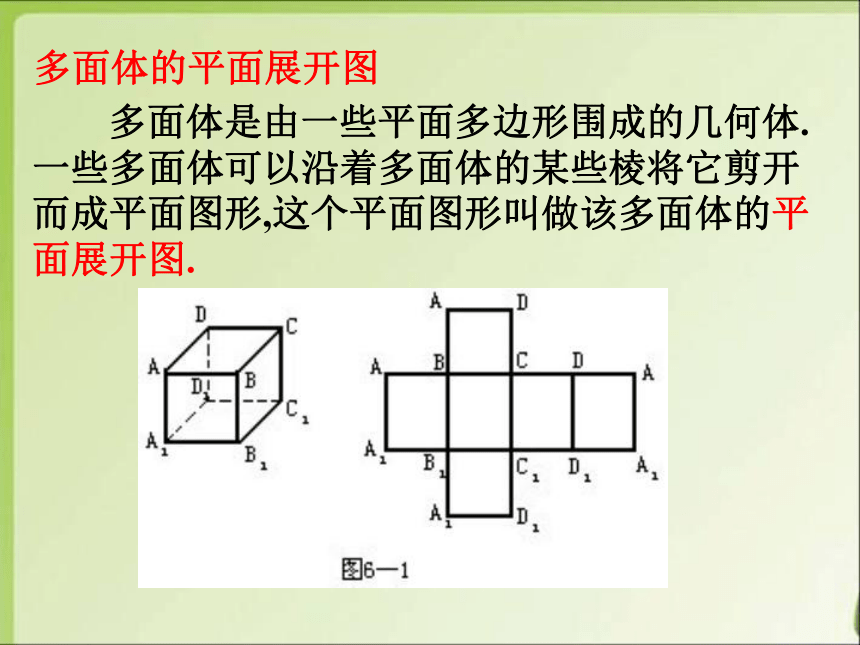
多面体的平面展开图
多面体是由一些平面多边形围成的几何体.一些多面体可以沿着多面体的某些棱将它剪开而成平面图形,这个平面图形叫做该多面体的平面展开图.
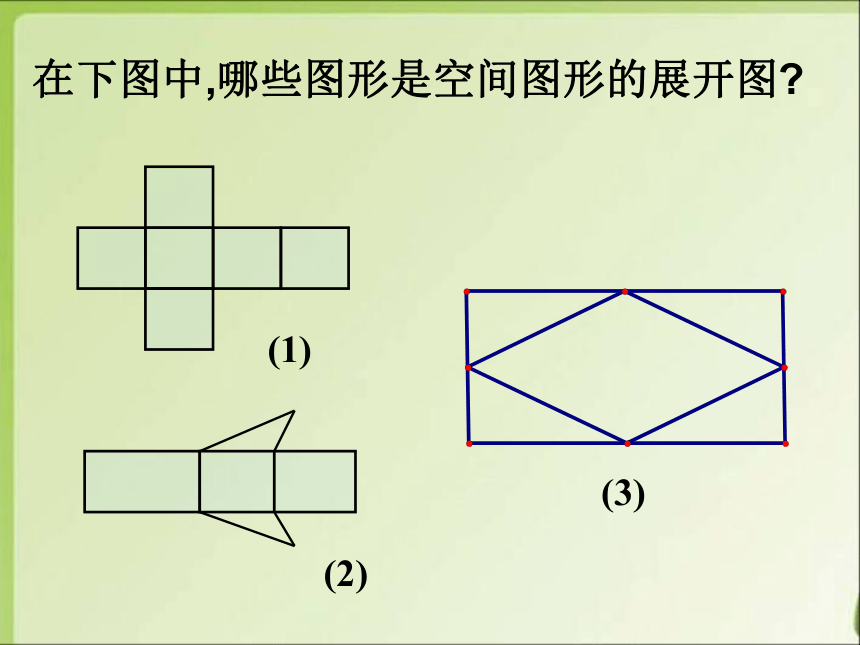
在下图中,哪些图形是空间图形的展开图
(1)
(2)
(3)
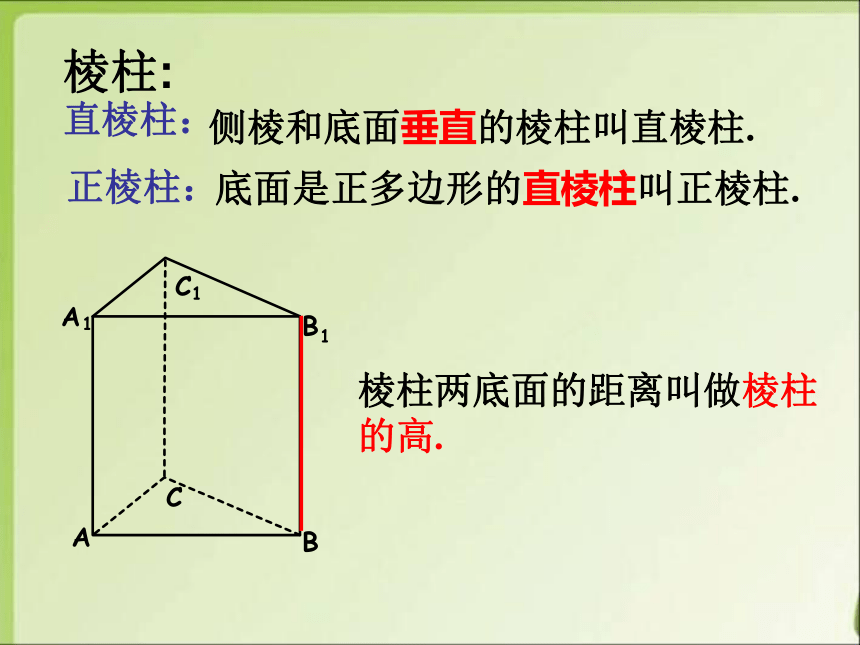
直棱柱:
正棱柱:
侧棱和底面垂直的棱柱叫直棱柱.
底面是正多边形的直棱柱叫正棱柱.
棱柱:
棱柱两底面的距离叫做棱柱的高.
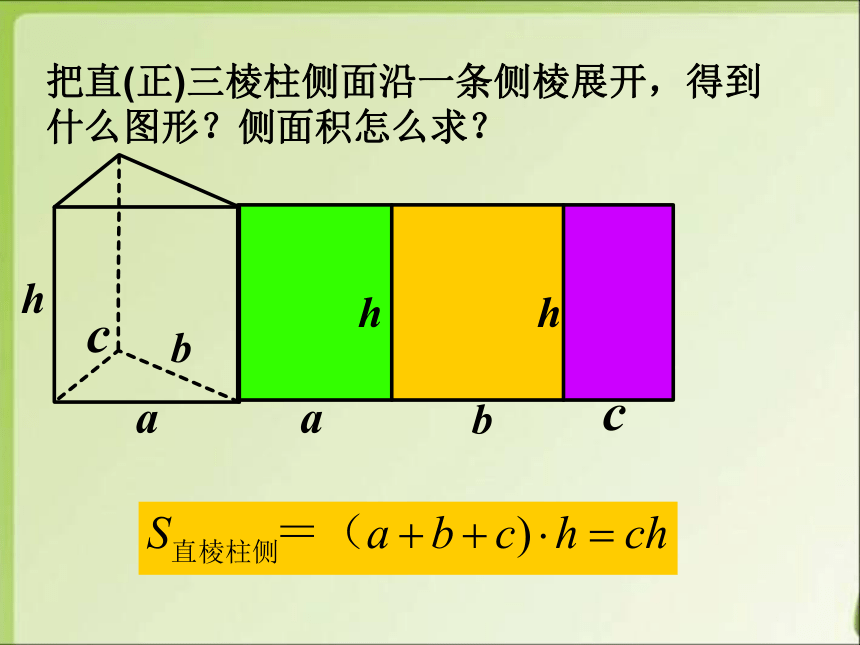
把直(正)三棱柱侧面沿一条侧棱展开,得到什么图形?侧面积怎么求?
C
O
B
A
P
D
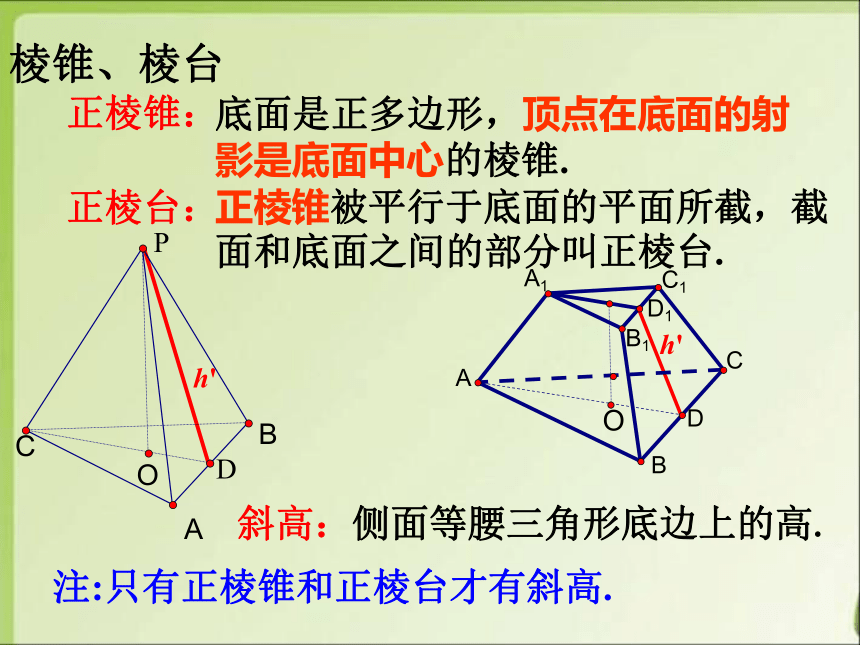
棱锥、棱台
正棱锥:
正棱台:
底面是正多边形,顶点在底面的射影是底面中心的棱锥.
正棱锥被平行于底面的平面所截,截面和底面之间的部分叫正棱台.
斜高:侧面等腰三角形底边上的高.
h'
h'
注:只有正棱锥和正棱台才有斜高.
C1
D1
A1
O
D
B
A
C
B1
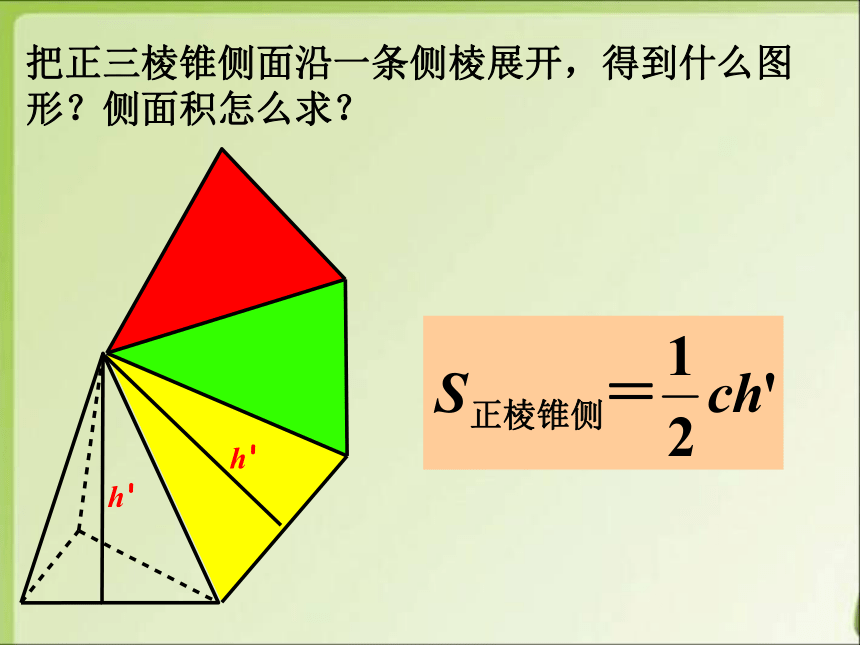
把正三棱锥侧面沿一条侧棱展开,得到什么图形?侧面积怎么求?
h'
h'
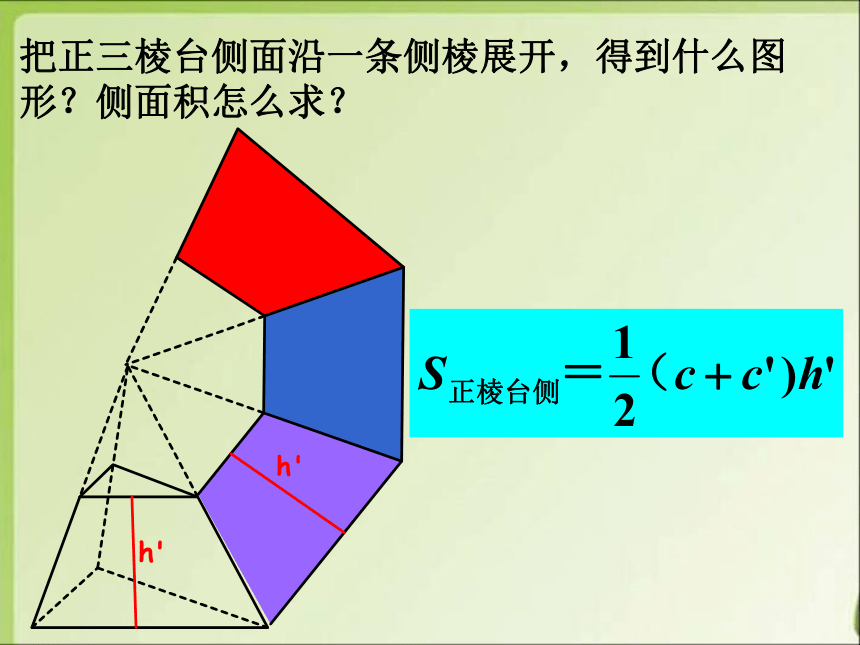
把正三棱台侧面沿一条侧棱展开,得到什么图形?侧面积怎么求?
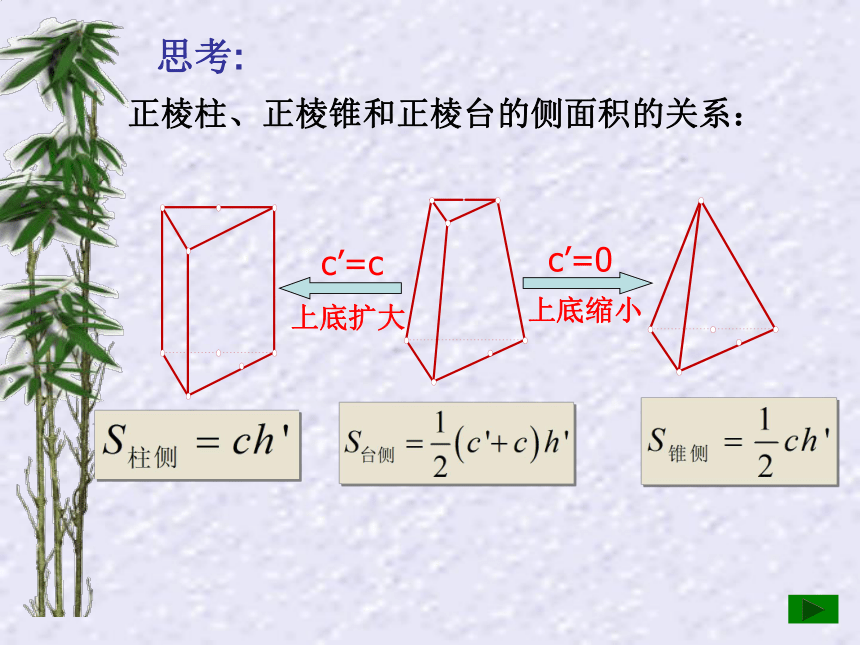
正棱柱、正棱锥和正棱台的侧面积的关系:
思考:
c’=c
上底扩大
c’=0
上底缩小
宽=
矩形
把圆柱的侧面沿着一条母线展开,得到什么图形 展开的图形与原图有什么关系?
扇形
把圆锥的侧面沿着一条母线展开,得到什么图形 展开的图形与原图有什么关系?
c
扇环
把圆台的侧面沿着一条母线展开,得到什么图形 展开的图形与原图有什么关系?
圆柱、圆锥、圆台的侧面积公式间的联系与区别
思考:
O
O’
O
O
r1=r2
上底扩大
r1=0
上底缩小
例1 设计一个正四棱锥形冷水塔塔顶,高是0.85m,底面的边长是1.5m,制造这种塔顶需要多少平方米的铁板?(保留两位有效数字)
解:如图,S表示塔的顶点,O表示底面中心,则SO是高,设SE是斜高。
在Rt△SOE中,由勾股定理得
SE=
E
S
O
数学运用
例2 有一根长为5cm,底面半径为1cm的圆柱形铁管,用一段铁丝在铁管上缠绕4圈,并使铁丝的两个端点落在圆柱的同一母线的两端,则铁丝的最短长度为多少厘米?(精确到0.1cm)
数学运用
分析: 可以把圆柱沿这条母线展开,将问题转化为平面几何的问题.
随堂练习:
1、已知正四棱柱的底面边长是3,侧面的对角线长是 ,求这个正四棱柱的侧面积。
2、求底面边长为2,高为1的正三棱锥的全面积。
3、下列图形中,不是正方体的展开图的是( )
A B C D
72
C
随堂练习:
4.如图,E,F分别为正方形ABCD的边BC,CD的中点,沿图中虚线折起来,它能围成怎样的几何体
A
F
E
C
D
B
5.用半径为r的半圆形铁皮卷成一个圆锥筒, 那么这个圆锥筒的高是多少 6.一个正三棱台的两个底面的边长分别等于8cm和18cm,侧棱长等于13cm,求它的侧面积.
三棱锥
468cm2
1、弄清楚柱、锥、台的侧面展开图的形状是关键;
S圆柱=2πrl
S圆锥=πrl
S圆台=π(r1+r2)l
r1=0
r1=r2
小结:
2、对应的侧面积公式
C’=C
C’=0
1.一个正三棱柱的底面是边长为5的正三角形,侧棱长为4,求其侧面积.
2.正四棱锥底面边长为6 ,高是4,中截面把棱锥截成一个小棱锥和一个棱台,求棱台的侧面积.
作业:
3.圆台的上、下底半径分别是10cm和20cm,它的侧面展开图的扇环的圆心角是1800,那么圆台的表面积是多少?(结果中保留π)
将立方体纸盒沿某些棱剪开,
并使六个面连在一起,然后铺平。
你能画出铺平后的图形吗?
(看谁画最多)
在长宽高分别是5米,4米,3米的长方体房间里,一只蚂蚁要从长方体的顶点A沿表面爬行到顶点C,怎样爬行路线最短?最短路程是多少
A
C
B
思考题
1.3.1空间几何体的表面积
多面体的平面展开图
多面体是由一些平面多边形围成的几何体.一些多面体可以沿着多面体的某些棱将它剪开而成平面图形,这个平面图形叫做该多面体的平面展开图.
在下图中,哪些图形是空间图形的展开图
(1)
(2)
(3)
直棱柱:
正棱柱:
侧棱和底面垂直的棱柱叫直棱柱.
底面是正多边形的直棱柱叫正棱柱.
棱柱:
棱柱两底面的距离叫做棱柱的高.
把直(正)三棱柱侧面沿一条侧棱展开,得到什么图形?侧面积怎么求?
C
O
B
A
P
D
棱锥、棱台
正棱锥:
正棱台:
底面是正多边形,顶点在底面的射影是底面中心的棱锥.
正棱锥被平行于底面的平面所截,截面和底面之间的部分叫正棱台.
斜高:侧面等腰三角形底边上的高.
h'
h'
注:只有正棱锥和正棱台才有斜高.
C1
D1
A1
O
D
B
A
C
B1
把正三棱锥侧面沿一条侧棱展开,得到什么图形?侧面积怎么求?
h'
h'
把正三棱台侧面沿一条侧棱展开,得到什么图形?侧面积怎么求?
正棱柱、正棱锥和正棱台的侧面积的关系:
思考:
c’=c
上底扩大
c’=0
上底缩小
宽=
矩形
把圆柱的侧面沿着一条母线展开,得到什么图形 展开的图形与原图有什么关系?
扇形
把圆锥的侧面沿着一条母线展开,得到什么图形 展开的图形与原图有什么关系?
c
扇环
把圆台的侧面沿着一条母线展开,得到什么图形 展开的图形与原图有什么关系?
圆柱、圆锥、圆台的侧面积公式间的联系与区别
思考:
O
O’
O
O
r1=r2
上底扩大
r1=0
上底缩小
例1 设计一个正四棱锥形冷水塔塔顶,高是0.85m,底面的边长是1.5m,制造这种塔顶需要多少平方米的铁板?(保留两位有效数字)
解:如图,S表示塔的顶点,O表示底面中心,则SO是高,设SE是斜高。
在Rt△SOE中,由勾股定理得
SE=
E
S
O
数学运用
例2 有一根长为5cm,底面半径为1cm的圆柱形铁管,用一段铁丝在铁管上缠绕4圈,并使铁丝的两个端点落在圆柱的同一母线的两端,则铁丝的最短长度为多少厘米?(精确到0.1cm)
数学运用
分析: 可以把圆柱沿这条母线展开,将问题转化为平面几何的问题.
随堂练习:
1、已知正四棱柱的底面边长是3,侧面的对角线长是 ,求这个正四棱柱的侧面积。
2、求底面边长为2,高为1的正三棱锥的全面积。
3、下列图形中,不是正方体的展开图的是( )
A B C D
72
C
随堂练习:
4.如图,E,F分别为正方形ABCD的边BC,CD的中点,沿图中虚线折起来,它能围成怎样的几何体
A
F
E
C
D
B
5.用半径为r的半圆形铁皮卷成一个圆锥筒, 那么这个圆锥筒的高是多少 6.一个正三棱台的两个底面的边长分别等于8cm和18cm,侧棱长等于13cm,求它的侧面积.
三棱锥
468cm2
1、弄清楚柱、锥、台的侧面展开图的形状是关键;
S圆柱=2πrl
S圆锥=πrl
S圆台=π(r1+r2)l
r1=0
r1=r2
小结:
2、对应的侧面积公式
C’=C
C’=0
1.一个正三棱柱的底面是边长为5的正三角形,侧棱长为4,求其侧面积.
2.正四棱锥底面边长为6 ,高是4,中截面把棱锥截成一个小棱锥和一个棱台,求棱台的侧面积.
作业:
3.圆台的上、下底半径分别是10cm和20cm,它的侧面展开图的扇环的圆心角是1800,那么圆台的表面积是多少?(结果中保留π)
将立方体纸盒沿某些棱剪开,
并使六个面连在一起,然后铺平。
你能画出铺平后的图形吗?
(看谁画最多)
在长宽高分别是5米,4米,3米的长方体房间里,一只蚂蚁要从长方体的顶点A沿表面爬行到顶点C,怎样爬行路线最短?最短路程是多少
A
C
B
思考题
