2012年中考数学专题:数学猜想与规律发现(附完整答案)
文档属性
| 名称 | 2012年中考数学专题:数学猜想与规律发现(附完整答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 259.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-26 00:00:00 | ||
图片预览


文档简介
中考数学专题复习:数学猜想与规律发现
归纳与猜想问题指的是给出一定条件(可以是有规律的算式、图形或图表),让学生认真分析,仔细观察,综合归纳,大胆猜想,得出结论,进而加以验证的数学探索题。其解题思维过程是:从特殊情况入手→探索发现规律→综合归纳→猜想得出结论→验证结论,这类问题有利于培养学生思维的深刻性和创造性。
一、知识网络图
二、基础知识整理
猜想规律型的问题难度相对为中等题,经常以填空等形式出现,解题时要善于从所提供的数字或图形信息中,寻找其共同之处,这个存在于个例中的共性,就是规律。其中蕴含着“特殊——一般——特殊”的常用模式,体现了总结归纳的数学思想,这也正是人类认识新生事物的一般过程。
相对而言,猜想结论型问题的难度较大些,具体题目往往是直观猜想与科学论证、具体
应用的结合,解题的方法也更为灵活多样:计算、验证、类比、比较、测量、绘图、移动等等,都能用到。由于猜想本身就是一种重要的数学方法,也是人们探索发现新知的重要手段,非常有利于培养创造性思维能力,所以备受命题专家的青睐,逐步成为中考的又一热点。
典型例题分析
1.(烟台09)如图,细心观察图形,认真分析各式,然后解答问题:
()2+1=2 S1= eq \f(,2)
()2+1=3 S2= eq \f(,2)
()2+1=4 S3= eq \f(,2)
⑴请用含有n(n是正整数)的等式表示上述变化规律;
⑵推算出OA10的长;
⑶求出S12+S22+S32+…+S102的值.
解:⑴()2+1=n+1,Sn= eq \f(,2);
⑵∵OA1=,OA2=,OA3=,…,∴OA10=;
⑶S12+S22+S32+…+S102=(1+2+3+…+10)=.
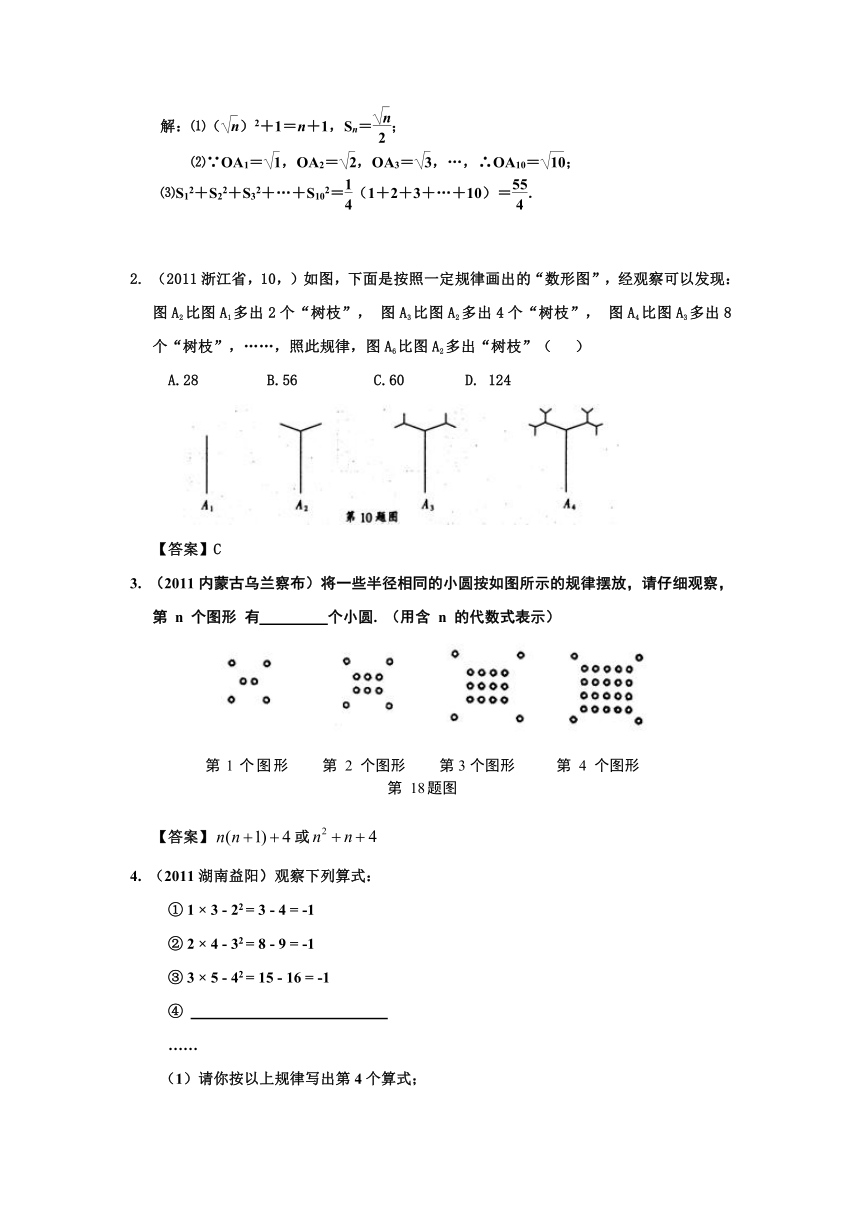
2. (2011浙江省,10,)如图,下面是按照一定规律画出的“数形图”,经观察可以发现:图A2比图A1多出2个“树枝”, 图A3比图A2多出4个“树枝”, 图A4比图A3多出8个“树枝”,……,照此规律,图A6比图A2多出“树枝”( )
A.28 B.56 C.60 D. 124
【答案】C
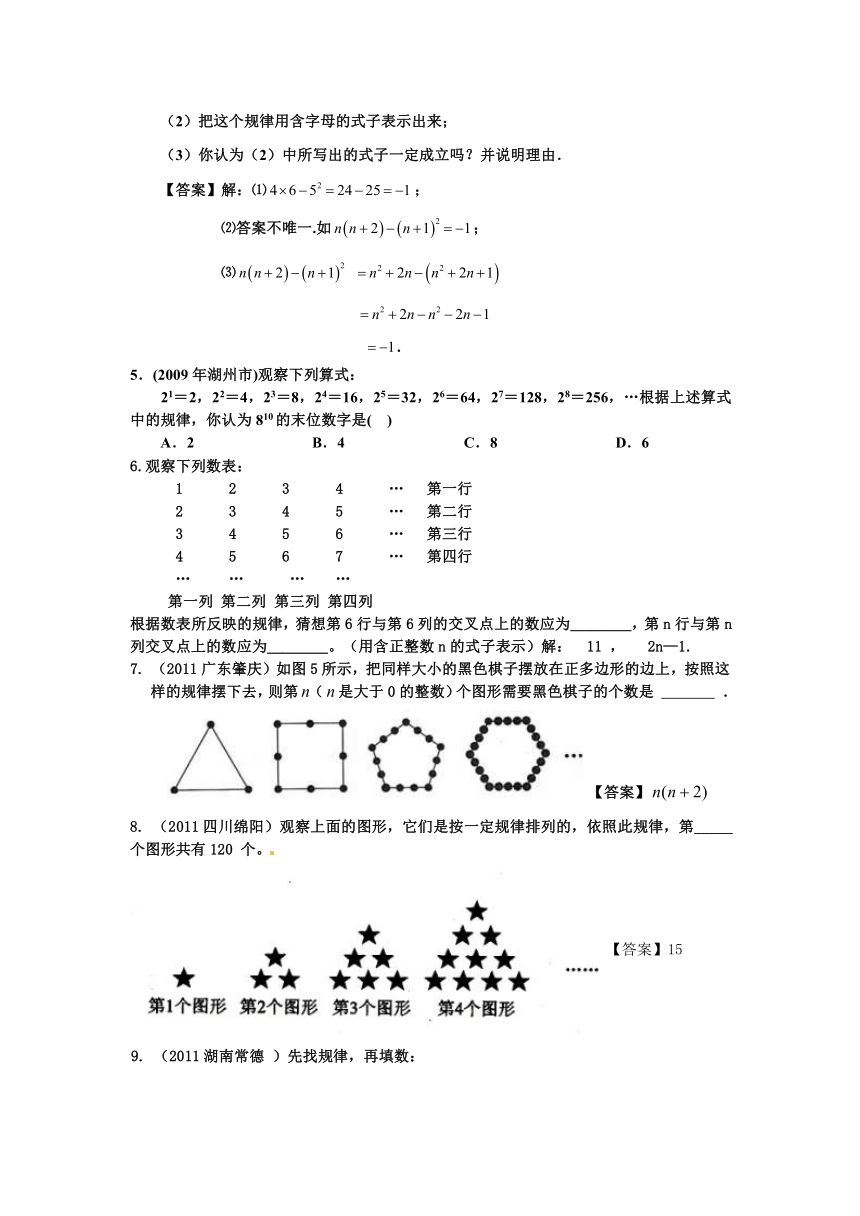
3. (2011内蒙古乌兰察布)将一些半径相同的小圆按如图所示的规律摆放,请仔细观察,第 n 个图形 有 个小圆. (用含 n 的代数式表示)
【答案】或
4. (2011湖南益阳)观察下列算式:
① 1 × 3 - 22 = 3 - 4 = -1
② 2 × 4 - 32 = 8 - 9 = -1
③ 3 × 5 - 42 = 15 - 16 = -1
④
……
(1)请你按以上规律写出第4个算式;
(2)把这个规律用含字母的式子表示出来;
(3)你认为(2)中所写出的式子一定成立吗?并说明理由.
【答案】解:⑴;
⑵答案不唯一.如;
⑶
.
5.(2009年湖州市)观察下列算式:
21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…根据上述算式中的规律,你认为810的末位数字是( )
A.2 B.4 C.8 D.6
6.观察下列数表:
1 2 3 4 … 第一行
2 3 4 5 … 第二行
3 4 5 6 … 第三行
4 5 6 7 … 第四行
… … … …
第一列 第二列 第三列 第四列
根据数表所反映的规律,猜想第6行与第6列的交叉点上的数应为____,第n行与第n列交叉点上的数应为____。(用含正整数n的式子表示)解: 11 , 2n—1.
7. (2011广东肇庆)如图5所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第(是大于0的整数)个图形需要黑色棋子的个数是 .
【答案】
8. (2011四川绵阳)观察上面的图形,它们是按一定规律排列的,依照此规律,第_____个图形共有120 个。
【答案】15
9. (2011湖南常德 )先找规律,再填数:
【答案】
10.(2011年浙江省杭州市模拟)如图,,过上到点的距离分别为的点作的垂线与相交,得到并标出一组黑色梯形,它们的面积分别为.观察图中的规律,求出第10个黑色梯形的面积( )
A.32 B.54 C.76 D.86
11.(2011年浙江杭州七模)图①是一块边长为1,周长记为P1的正三角形纸板,沿图①的底边剪去一块边长为的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪如图掉正三角形纸板边长的)后,得图③,④,…,记第n(n≥3) 块纸板的周长为Pn,则Pn-Pn-1的值为( )
A. B.
C. D.
答案:C
12.(2011年黄冈中考调研六)瑞士的一位中学教师巴尔末从光谱数据,,,,中,成功地发现了其规律,从而得到了巴尔末公式,继而打开了光谱奥妙的大门.请你根据这个规律写出第9个数 答案
13.(2011年浙江杭州三模)如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(―1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点P第100次跳动至点P100的坐标是 。
答案:(26,50)
14.(茂名2011模拟)一串有趣的图案按一定的规律排列(如图):
按此规律在右边的圆中画出的第2011个图案: 。答案:
15.(2011年广东省澄海实验学校模拟)根据图中箭头的指向的规律,从2007到2008再到2009,箭头的方向是以下图示中的( )
…
答案:C
16.(2011深圳模拟)如图,△ABC中,∠ACB=90°,∠B=30°,AC=1,过点C作CD1⊥AB于D1,过点D1作D1D2⊥BC于D2,过点D2作D2D3⊥AB于D3,这样继续作下去,线段DnDn+1(n为整数)等于( )
A、 B、 C、 D、
答案:D
17.(2011年重庆江津区七校联考一模)观察下列各式:……请你将猜想到的规律用含自然数n(n≥1)的代数式表示出来是_________ _.答案:
18. (2011杭州上城区一模)如图是与杨辉三角有类似性质的三角形数垒,
是相邻两行的前四个数(如图所示),
那么当a=8时, , .
答案:9,37
19.(2011年黄冈浠水模拟)下面是用棋子摆成的“上”字:
第一个“上”字 第二个“上”字 第三个“上”字
如果按照以上规律继续摆下去,那么通过观察,可以发现:第n个“上”字需用 棋子.答案:
20.(2011年北京四中3模)如下图,第(1)个多边形由正三角形“扩展”而来,边数记为a3,第(2)个多边形由正方形“扩展”而来,边数记为a4,……以此类推,由正n边形“扩展”而来的多边形的边数记为an(n≥3),则a6= ,当时,则n= 。
答案:42;100
21.(2010重庆)有两个完全重合的矩形,将其中一个始终保持不动,另一个矩形绕其对称中心O按逆时针方向进行旋转,每次均旋转45°,第1次旋转后得到图①,第2次旋转后得到图②,……,则第10次旋转后得到的图形与图①~④中相同的是( )
A. 图① B. 图② C. 图③ D. 图④
【分析】规律的归纳:通过观察图形可以看到每转动4次后便可重合,即4次一个循环,10÷4=2…2,所以应和图②相同.
【解答】B
22.(2010年山东青岛中考题)如图1,是用棋子摆成的图案,摆第1个图案需要7枚棋子,摆第2个图案需要19枚棋子,摆第3个图案需要37枚棋子,按照这样的方式摆下去,则摆第6个图案需要 枚棋子,摆第n个图案需要 枚棋子.
23. (2011山东济宁)观察下面的变形规律:
=1-; =-;=-;……
解答下面的问题:
(1)若n为正整数,请你猜想= ;
(2)证明你猜想的结论;
(3)求和:+++…+ .
【答案】(1) (2)证明:-=-==.
(3)原式=1-+-+-+…+-
=.
深圳中考近5年真题与模拟
1.(09深圳高级中学)观察下列各式:0,x,x2,2x3,3x4,5x5,8x6,…….试按此规律写出的第8个式子是_______。
2.(07年深圳中考)邓老师设计了一个计算程序,输入和输出的数据如下表:
输入数据 1 2 3 4 5 6 …
输出数据 …
那么,当输入数据是时,输出的数据是 .
3.(深圳中考09)已知依据上述规律,则 .
4.(深圳中考2010)观察下列算式,用你所发现的规律得出22010的末位数字是
21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…,
A.2 B.4 C.6 D.8
5.(深圳中考2011)如图6,这是由边长为1的等边三角形摆出的一系列图形,按这种方式摆下去,则第n个图形的周长是=______________________。
(1) (2) (3) (4) ……
图6
6.(深圳中考2011十校联考)如图6,,过上到点的距离分别为的点作的垂线与相交,得到并标出一组黑色梯形,它们的面积分别为.观察图中的规律,
求出第10个黑色梯形的面积 .
7.(08深圳中考)观察表一,寻找规律.表二、表三分别是从表一中截取的
一部分,其中a+b的值为_____________.
1 2 3 4 …
2 4 6 8 …
3 6 9 12 …
4 8 12 16 …
… … … … …
20 24
25 b
12
15
a
8.(2010年深圳宝安)用灰白两色正方形瓷砖铺设地面,第6个图案中灰色瓷砖块数为_____.
猜想性问题
猜想规律型
猜想结论型
猜想数式规律
猜想图形规律
猜想数值结果
猜想数量关系
猜想变化情况
A6
…
A5
1
1
A4
1
A3
A2
1
A1
1
O
S1
S2
S3
S4
S5
第1个图形
第 2 个图形
第3个图形
第 4 个图形
第 18题图
(第11题图)
…
① ② ③
……
9
0
1
2
5
6
10
8
7
4
3
D
C
A
B
16题图
(第18题)
…
图1
……
0
1
3
5
7
9
11
13
S1
S2
S3
S4
图6
表一 表二 表三
第1个图案
第2个图案
第3个图案
(第8题)
归纳与猜想问题指的是给出一定条件(可以是有规律的算式、图形或图表),让学生认真分析,仔细观察,综合归纳,大胆猜想,得出结论,进而加以验证的数学探索题。其解题思维过程是:从特殊情况入手→探索发现规律→综合归纳→猜想得出结论→验证结论,这类问题有利于培养学生思维的深刻性和创造性。
一、知识网络图
二、基础知识整理
猜想规律型的问题难度相对为中等题,经常以填空等形式出现,解题时要善于从所提供的数字或图形信息中,寻找其共同之处,这个存在于个例中的共性,就是规律。其中蕴含着“特殊——一般——特殊”的常用模式,体现了总结归纳的数学思想,这也正是人类认识新生事物的一般过程。
相对而言,猜想结论型问题的难度较大些,具体题目往往是直观猜想与科学论证、具体
应用的结合,解题的方法也更为灵活多样:计算、验证、类比、比较、测量、绘图、移动等等,都能用到。由于猜想本身就是一种重要的数学方法,也是人们探索发现新知的重要手段,非常有利于培养创造性思维能力,所以备受命题专家的青睐,逐步成为中考的又一热点。
典型例题分析
1.(烟台09)如图,细心观察图形,认真分析各式,然后解答问题:
()2+1=2 S1= eq \f(,2)
()2+1=3 S2= eq \f(,2)
()2+1=4 S3= eq \f(,2)
⑴请用含有n(n是正整数)的等式表示上述变化规律;
⑵推算出OA10的长;
⑶求出S12+S22+S32+…+S102的值.
解:⑴()2+1=n+1,Sn= eq \f(,2);
⑵∵OA1=,OA2=,OA3=,…,∴OA10=;
⑶S12+S22+S32+…+S102=(1+2+3+…+10)=.
2. (2011浙江省,10,)如图,下面是按照一定规律画出的“数形图”,经观察可以发现:图A2比图A1多出2个“树枝”, 图A3比图A2多出4个“树枝”, 图A4比图A3多出8个“树枝”,……,照此规律,图A6比图A2多出“树枝”( )
A.28 B.56 C.60 D. 124
【答案】C
3. (2011内蒙古乌兰察布)将一些半径相同的小圆按如图所示的规律摆放,请仔细观察,第 n 个图形 有 个小圆. (用含 n 的代数式表示)
【答案】或
4. (2011湖南益阳)观察下列算式:
① 1 × 3 - 22 = 3 - 4 = -1
② 2 × 4 - 32 = 8 - 9 = -1
③ 3 × 5 - 42 = 15 - 16 = -1
④
……
(1)请你按以上规律写出第4个算式;
(2)把这个规律用含字母的式子表示出来;
(3)你认为(2)中所写出的式子一定成立吗?并说明理由.
【答案】解:⑴;
⑵答案不唯一.如;
⑶
.
5.(2009年湖州市)观察下列算式:
21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…根据上述算式中的规律,你认为810的末位数字是( )
A.2 B.4 C.8 D.6
6.观察下列数表:
1 2 3 4 … 第一行
2 3 4 5 … 第二行
3 4 5 6 … 第三行
4 5 6 7 … 第四行
… … … …
第一列 第二列 第三列 第四列
根据数表所反映的规律,猜想第6行与第6列的交叉点上的数应为____,第n行与第n列交叉点上的数应为____。(用含正整数n的式子表示)解: 11 , 2n—1.
7. (2011广东肇庆)如图5所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第(是大于0的整数)个图形需要黑色棋子的个数是 .
【答案】
8. (2011四川绵阳)观察上面的图形,它们是按一定规律排列的,依照此规律,第_____个图形共有120 个。
【答案】15
9. (2011湖南常德 )先找规律,再填数:
【答案】
10.(2011年浙江省杭州市模拟)如图,,过上到点的距离分别为的点作的垂线与相交,得到并标出一组黑色梯形,它们的面积分别为.观察图中的规律,求出第10个黑色梯形的面积( )
A.32 B.54 C.76 D.86
11.(2011年浙江杭州七模)图①是一块边长为1,周长记为P1的正三角形纸板,沿图①的底边剪去一块边长为的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪如图掉正三角形纸板边长的)后,得图③,④,…,记第n(n≥3) 块纸板的周长为Pn,则Pn-Pn-1的值为( )
A. B.
C. D.
答案:C
12.(2011年黄冈中考调研六)瑞士的一位中学教师巴尔末从光谱数据,,,,中,成功地发现了其规律,从而得到了巴尔末公式,继而打开了光谱奥妙的大门.请你根据这个规律写出第9个数 答案
13.(2011年浙江杭州三模)如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(―1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点P第100次跳动至点P100的坐标是 。
答案:(26,50)
14.(茂名2011模拟)一串有趣的图案按一定的规律排列(如图):
按此规律在右边的圆中画出的第2011个图案: 。答案:
15.(2011年广东省澄海实验学校模拟)根据图中箭头的指向的规律,从2007到2008再到2009,箭头的方向是以下图示中的( )
…
答案:C
16.(2011深圳模拟)如图,△ABC中,∠ACB=90°,∠B=30°,AC=1,过点C作CD1⊥AB于D1,过点D1作D1D2⊥BC于D2,过点D2作D2D3⊥AB于D3,这样继续作下去,线段DnDn+1(n为整数)等于( )
A、 B、 C、 D、
答案:D
17.(2011年重庆江津区七校联考一模)观察下列各式:……请你将猜想到的规律用含自然数n(n≥1)的代数式表示出来是_________ _.答案:
18. (2011杭州上城区一模)如图是与杨辉三角有类似性质的三角形数垒,
是相邻两行的前四个数(如图所示),
那么当a=8时, , .
答案:9,37
19.(2011年黄冈浠水模拟)下面是用棋子摆成的“上”字:
第一个“上”字 第二个“上”字 第三个“上”字
如果按照以上规律继续摆下去,那么通过观察,可以发现:第n个“上”字需用 棋子.答案:
20.(2011年北京四中3模)如下图,第(1)个多边形由正三角形“扩展”而来,边数记为a3,第(2)个多边形由正方形“扩展”而来,边数记为a4,……以此类推,由正n边形“扩展”而来的多边形的边数记为an(n≥3),则a6= ,当时,则n= 。
答案:42;100
21.(2010重庆)有两个完全重合的矩形,将其中一个始终保持不动,另一个矩形绕其对称中心O按逆时针方向进行旋转,每次均旋转45°,第1次旋转后得到图①,第2次旋转后得到图②,……,则第10次旋转后得到的图形与图①~④中相同的是( )
A. 图① B. 图② C. 图③ D. 图④
【分析】规律的归纳:通过观察图形可以看到每转动4次后便可重合,即4次一个循环,10÷4=2…2,所以应和图②相同.
【解答】B
22.(2010年山东青岛中考题)如图1,是用棋子摆成的图案,摆第1个图案需要7枚棋子,摆第2个图案需要19枚棋子,摆第3个图案需要37枚棋子,按照这样的方式摆下去,则摆第6个图案需要 枚棋子,摆第n个图案需要 枚棋子.
23. (2011山东济宁)观察下面的变形规律:
=1-; =-;=-;……
解答下面的问题:
(1)若n为正整数,请你猜想= ;
(2)证明你猜想的结论;
(3)求和:+++…+ .
【答案】(1) (2)证明:-=-==.
(3)原式=1-+-+-+…+-
=.
深圳中考近5年真题与模拟
1.(09深圳高级中学)观察下列各式:0,x,x2,2x3,3x4,5x5,8x6,…….试按此规律写出的第8个式子是_______。
2.(07年深圳中考)邓老师设计了一个计算程序,输入和输出的数据如下表:
输入数据 1 2 3 4 5 6 …
输出数据 …
那么,当输入数据是时,输出的数据是 .
3.(深圳中考09)已知依据上述规律,则 .
4.(深圳中考2010)观察下列算式,用你所发现的规律得出22010的末位数字是
21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…,
A.2 B.4 C.6 D.8
5.(深圳中考2011)如图6,这是由边长为1的等边三角形摆出的一系列图形,按这种方式摆下去,则第n个图形的周长是=______________________。
(1) (2) (3) (4) ……
图6
6.(深圳中考2011十校联考)如图6,,过上到点的距离分别为的点作的垂线与相交,得到并标出一组黑色梯形,它们的面积分别为.观察图中的规律,
求出第10个黑色梯形的面积 .
7.(08深圳中考)观察表一,寻找规律.表二、表三分别是从表一中截取的
一部分,其中a+b的值为_____________.
1 2 3 4 …
2 4 6 8 …
3 6 9 12 …
4 8 12 16 …
… … … … …
20 24
25 b
12
15
a
8.(2010年深圳宝安)用灰白两色正方形瓷砖铺设地面,第6个图案中灰色瓷砖块数为_____.
猜想性问题
猜想规律型
猜想结论型
猜想数式规律
猜想图形规律
猜想数值结果
猜想数量关系
猜想变化情况
A6
…
A5
1
1
A4
1
A3
A2
1
A1
1
O
S1
S2
S3
S4
S5
第1个图形
第 2 个图形
第3个图形
第 4 个图形
第 18题图
(第11题图)
…
① ② ③
……
9
0
1
2
5
6
10
8
7
4
3
D
C
A
B
16题图
(第18题)
…
图1
……
0
1
3
5
7
9
11
13
S1
S2
S3
S4
图6
表一 表二 表三
第1个图案
第2个图案
第3个图案
(第8题)
同课章节目录
