2012年中考数学专题:函数、一次函数、反比例函数
文档属性
| 名称 | 2012年中考数学专题:函数、一次函数、反比例函数 |

|
|
| 格式 | zip | ||
| 文件大小 | 415.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-26 00:00:00 | ||
图片预览




文档简介
2012中考数学专题复习:函数、一次函数、反比例函数综合
【知识分析回顾】
1.函数定义:在某一变化过程中,存在两个变量x,y,变量x在某一范围内取每一个确定的值,y都有唯一确定的值与之对应,则称y是x的____ _,其中x为_______量。
2.函数自变量的取值范围:指使函数本身有意义并且符合实际情况的_____ __的取值范围。
3.函数的表示法(三种):
(1)关系式法:用代数方法表示两个变量之间的关系,如y=(x≥),从方程角度上讲,函数实质上就是一个______ _;
(2)图象法:如心电路图,则表示两个变量时间和心跳次数之间的函数关系;
(3)列表法:用表格方式表示两个变量之间的关系,如你的成绩通知单表,表示的是你的科目与成绩两个变量的关系;
(4)以上三种函数表示法之间的关系:
函数的解析式(二元方程)列表法得到点的坐标(二元方程的无数个解)顺次连结各点得到函数图象,根据函数图象可研究这一函数的有关性质,以便应用。
4.平面直角坐标系 (1)各象限内点的坐标的特点 (2)坐标轴上点的坐标的特点
(3)关于坐标轴、原点对称的点的坐标的特点
5.运动是绝对的,静止是相对的,世间上任何事物都是发展变化的.而函数就是研究两个变量之间的关系,正因为是变化的,又是数形结合,所以掌握本章知识较难,同学们在复习时要始终抓着方程(方程的解) 点的坐标 函数图象与性质这个网,综合几何代数知识,用数形结合法来解题。
6.正比例函数的定义、图象和性质:
(1)定义:形如y=kx (k为常数,k≠0)的函数叫做正比例函数。
(2)图象:一条经过原点的直线。
(3)性质: 当k>0时,y随x的增大而 ;当k<0时,y随x的增大而 。
7.一次函数的定义、图象和性质:
(1)定义:形如y=kx+b(k,b为常数,k≠0)的函数叫做一次函数
(2)图象: y=kx+b的图象是一条 ,因为两点确定一条直线,所以在画图象时,任取你喜欢的两个点,过这两点即可画出直线。
(3)性质:k的符号看直线通过一、三或二、四象限而定,b的符号看直线在y轴上的截距而定。当k>0时,y随x的增大而 ;当k<0时,y随x的增大而 。
8.反比例函数:
(1)定义:形如y=(k为常数,k≠0)叫做反比例函数。自变量x≠0,函数与x轴、y轴无交点。
(2)图象:双曲线,在用描点法画反比例函数y=的图象时,应注意自变量x的取值不能为0,应从1或-1开始对称取点.
(3)性质:当k>0时,图象位于________象限,在每一个象限内,y随x的增大而________:
当k<0时,图象位于________象限,在每一个象限内,y随x的增大而________。
(4)两支曲线无限接近与坐标轴但永远不会与坐标轴相交。
9. 反比例函数的图象和性质
k的符号 k>0 k<0
图像的大致位置
经过象限 第 象限 第 象限
性质 在每一象限内,y随x的增大而 在每一象限内,y随x的增大而
10.的几何含义:反比例函数y= (k≠0)中比例系数k的几何意义,即过双曲线y= (k≠0)上任意一点P作x轴、y轴垂线,设垂足分别为A、B,则所得矩形OAPB的面积=
【典型例题分析】
1. (2010湖北孝感,7,3分)一艘轮船在长江航线上往返于甲、乙两地.若轮船在静水中的速度不变,轮船先从甲地顺水航行到乙地,停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用的时间为t(小时),航行的路程为s(千米),则s与t的函数图象大致是( )
【答案】B
2.(2010年浙江省东阳县)汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程看作时间的函数,其图像可能是( )
A B C D
3.已知一次函数的图像经过原点,则k的值为 ( )
(A)1; (B)-1; (C)0; (D).
4. (2011广东清远,9,3分)一次函数的图象大致是( )
【答案】A
5. (2011广东广州市)当实数x的取值使得有意义时,函数y=4x+1中y的取值范围是( ).
A.y≥-7 B.y≥9 C.y>9 D.y≤9 【答案】B
6. (2011山东日照,9,4分)在平面直角坐标系中,已知直线y=-x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )
(A)(0,) (B)(0,) (C)(0,3) (D)(0,4)
【答案】B
7.(2010深圳).升旗时,旗子的高度h(米)与时间t(分)的函数图像大致为( )
8. (2011贵州遵义 )若一次函数的函数值随的增大而减小,则的取值范围是
A. B. C. D. 【答案】D
9. (2011山东泰安,13 ,3分)已知一次函数y=mx+n-2的图像如图所示,则m、n的取值范围是( )
A.m>0,n<2 B. m>0,n>2
C. m<0,n<2 D. m<0,n>2
【答案】D
10. ( 2011重庆江津, 4,4分)直线y=x-1的图像经过象限是( )
A.第一、二、三象限 B.第一、二、四象限
C.第二、三、四象限 D.第一、三、四象限
11. (2011浙江杭州 )一个矩形被直线分成面积为x,y的两部分,则y与x之间的函数关系只可能是
【答案】A
12. (2011浙江省,9,3分)如图,在平面直角坐标系中,线段AB的端点坐标为A(-2,4),B(4,2),直线y=kx-2与线段AB有交点,则k的值不可能是( )
A.-5 B.-2 C.3 D. 5
13. (2011江西 )已知一次函数y=x+b的图像经过一、二、三象限,则b的值可以是( ).
A.-2 B.-1 C.0 D.2 【答案】D
14. (2011江苏苏州,10,3分)如图,已知A点坐标为(5,0),直线y=x+b(b>0)与
y轴交于点B,连接AB,∠α=75°,则b的值为( )
A.3 B. C.4 D.
【答案】B
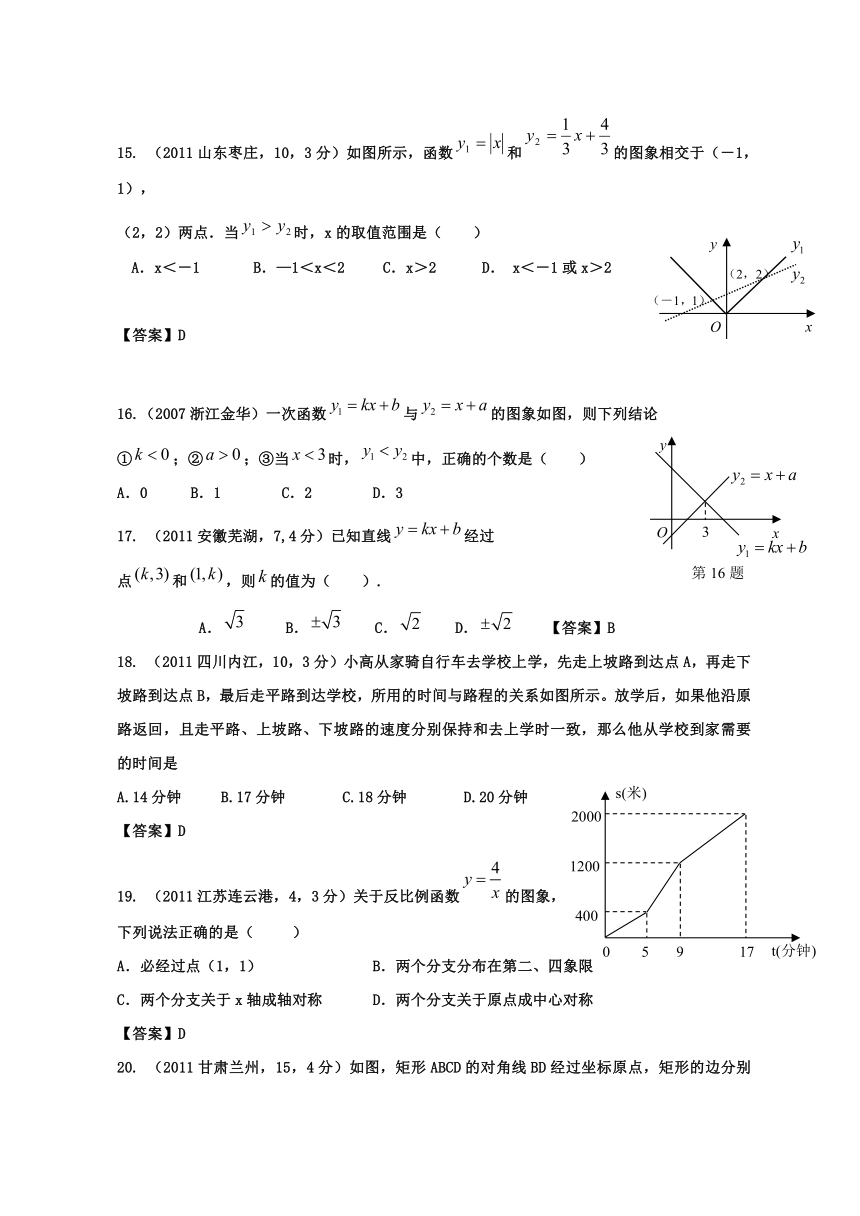
15. (2011山东枣庄,10,3分)如图所示,函数和的图象相交于(-1,1),
(2,2)两点.当时,x的取值范围是( )
A.x<-1 B.—1<x<2 C.x>2 D. x<-1或x>2
【答案】D
16.(2007浙江金华)一次函数与的图象如图,则下列结论
①;②;③当时,中,正确的个数是( )
A.0 B.1 C.2 D.3
17. (2011安徽芜湖,7,4分)已知直线经过
点和,则的值为( ).
A. B. C. D. 【答案】B
18. (2011四川内江,10,3分)小高从家骑自行车去学校上学,先走上坡路到达点A,再走下坡路到达点B,最后走平路到达学校,所用的时间与路程的关系如图所示。放学后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上学时一致,那么他从学校到家需要的时间是
A.14分钟 B.17分钟 C.18分钟 D.20分钟
【答案】D
19. (2011江苏连云港,4,3分)关于反比例函数的图象,
下列说法正确的是( )
A.必经过点(1,1) B.两个分支分布在第二、四象限
C.两个分支关于x轴成轴对称 D.两个分支关于原点成中心对称
【答案】D
20. (2011甘肃兰州,15,4分)如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数的图象上。若点A的坐标为(-2,-2),则k的值为( )
A.1 B.-3 C.4 D.1或-3
【答案】D
21.(2010年山东省青岛市)函数与(a≠0)
在同一直角坐标系中的图象可能是( ).
A. B. C. D.
22.(2010年安徽省芜湖市)二次函数y=ax2+bx+c的图象如图所示,反比例函数y= 与正比例函数y=(b+c)x在同一坐标系中的大致图象可能是( )
A. B. C. D.
23.(2010年四川省眉山)如图,已知双曲线经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(,4),则△AOC的面积为( )
A.12 B.9 C.6 D.4
24.(2010年宁德市)反比例函数(x>0)的图象如图所示,随着x值的增大,y值( ).
A.减小 B.增大 C.不变 D.先减小后不变
【答案】A
25. (2010年兰州市) 已知点(-1,),(2,),(3,)在
反比例函数的图像上. 下列结论中正确的是( )
A. B. C. D.
26.(2009湖南岳阳)在下图中,反比例函数的图象大致是( )
27.(2009福建龙岩)函数与在同一坐标系内的图象可以是( )
28. (2011湖南怀化,5,3分)函数与函数在同一坐标系中的大致图像是( )
【答案】D
29.(2010深圳)如图2,点P(3a,a)是反比例函y=(k>0)与⊙O的
一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
A.y= B.y= C.y= D.y=
30.(2011深圳)如图7,△ABC的内心在y轴上,点C的坐标为(2,0),点B的坐标
为(0,2),直线AC的解析式为:,则tanA的值是_________。
31.(09深圳)如图,反比例函数的图象与直线的交点
为A,B,过点A作y轴的平行线与过点B作x轴的平
行线相交于点C,则的面积为( )
A.8 B.6 C.4 D.2
32.(08深圳).如图3,直线OA与反比例函数的图象在第一象限交于A点,AB⊥x轴于点B,△OAB的面积为2,则k=
33. (2011湖北黄石,3,3分)若双曲线y=的图象
经过第二、四象限,则k的取值范围是( )
A.k> B. k< C. k= D. 不存在 【答案】B
34. (2011山东威海,5,3分)下列各点中,在函数图象上的是( )
A.(-2,-4) B.(2,3) C.(-1,6) D.
【答案】C
35. (2011浙江台州)如图,反比例函数的图象与一次函数的图象交于点M,N,已点M的坐标为(1,3),点N的纵坐标为-1,根据图象信息可得关于x的方程=的解为( )
A. -3,1 B. -3,3 C. -1,1 D.3,-1
【答案】A
36. ( 2011重庆江津, 6,4分)已知如图,A是反比例函数的图像上的一点,
AB⊥x轴于点B,且△ABO的面积是3,则k的值是( )
A.3 B.-3 C.6 D.-6 【答案】C
37. (2011湖北黄冈,4,3分)如图:点A在双曲线上,AB⊥x
轴于B,且△AOB的面积S△AOB=2,则k=______.
38. (2011浙江衢州)在直角坐标系中,有如图所示的轴于点,斜边,反比例函数的图像经过的中点,且与交于点,则点的坐标为 . 【答案】
39. (2011广东株洲)如图,直线l过A、B两点,
A(,),B(,),则直线l的解析式为 .
【答案】y=x-1
40.(2011四川成都,21,4分)在平面直角坐标系中,点P(2,)在正比例函数的图象上,则点Q()位于第______象限. 【答案】四.
41. (2011湖南怀化,12,3分)一次函数y=-2x+3中,y的值随x值增大而___________.(填“增大”或“减小”) 【答案】减小
42. (2011山东日照,22,9分)某商业集团新进了40台空调机,60台电冰箱,计划调配给下属的甲、乙两个连锁店销售,其中70台给甲连锁店,30台给乙连锁店.两个连锁店销售这两种电器每台的利润(元)如下表:
空调机 电冰箱
甲连锁店 200 170
乙连锁店 160 150
设集团调配给甲连锁店x台空调机,集团卖出这100台电器的总利润为y(元).
(1)求y关于x的函数关系式,并求出x的取值范围;
(2)为了促销,集团决定仅对甲连锁店的空调机每台让利a元销售,其他的销售利润不变,并且让利后每台空调机的利润仍然高于甲连锁店销售的每台电冰箱的利润,问该集团应该如何设计调配方案,使总利润达到最大?
【答案】 (1)根据题意知,调配给甲连锁店电冰箱(70-x)台,
调配给乙连锁店空调机(40-x)台,电冰箱(x-10)台, 则y=200x+170(70-x)+160(40-x)+150(x-10),
即y=20x+16800.∵
∴10≤x≤40. ∴y=20x+168009 (10≤x≤40);
(2)按题意知:y=(200-a)x+170(70-x)+160(40-x)+150(x-10),
即y=(20-a)x+16800. ∵200-a>170,∴a<30.
当0<a<20时,x=40,即调配给甲连锁店空调机40台,电冰箱30台,乙连锁店空调0台,
电冰箱30台; 当a=20时,x的取值在10≤x≤40内的所有方案利润相同;
当20<a<30时,x=10,即调配给甲连锁店空调机10台,电冰箱60台,乙连锁店空调30台,电冰箱0台;
43. (2011湖北宜昌,19,7分)某市实施“限塑令”后,2008年大约减少塑料消耗约4万吨.调查分析结果显示,从2008年开始,五年内该市因实施“限塑令”而减少的塑料消耗量y(万吨)随着时间(年)逐年成直线上升,y与之间的关系如图所示.
(1)求y与之间的关系式;
(2)请你估计,该市2011年因实施“限塑令”而减少的塑料消耗量为多少
(第43题图)
【答案】解:(1)设y=kx+b. (1分)由题意,得2008k+b=4,(2分)2010k+b=6,(3分).
解得k=1(4分)b=-2004(5分)∴y=x-2004.(2)当x=2011时,y=2011-2004(6分)=7.(7分)∴该市2011年因“限塑令”而减少的塑料消耗量约为7万吨.
o
y
x
y
x
o
t
h
O
t
h
O
t
h
O
t
h
O
A
B
C
D
(-1,1)
(2,2)
x
y
O
x
y
O
3
第16题
400
0
5
9
17
1200
2000
s(米)
t(分钟)
x
y
O
A
B
C
D
y
x
O
y
x
O
x
y
O
x
O
y
x
y
O
第24题图
x
y
O
A.
x
y
O
B.
x
y
O
C.
x
y
O
D.
x
O
y
P
图2
A
B
C
30题
x
y
O
A
O
B
C
y
o
A
B
x
第36题图
A
B
O
x
y
第37题图
(第38题)
【知识分析回顾】
1.函数定义:在某一变化过程中,存在两个变量x,y,变量x在某一范围内取每一个确定的值,y都有唯一确定的值与之对应,则称y是x的____ _,其中x为_______量。
2.函数自变量的取值范围:指使函数本身有意义并且符合实际情况的_____ __的取值范围。
3.函数的表示法(三种):
(1)关系式法:用代数方法表示两个变量之间的关系,如y=(x≥),从方程角度上讲,函数实质上就是一个______ _;
(2)图象法:如心电路图,则表示两个变量时间和心跳次数之间的函数关系;
(3)列表法:用表格方式表示两个变量之间的关系,如你的成绩通知单表,表示的是你的科目与成绩两个变量的关系;
(4)以上三种函数表示法之间的关系:
函数的解析式(二元方程)列表法得到点的坐标(二元方程的无数个解)顺次连结各点得到函数图象,根据函数图象可研究这一函数的有关性质,以便应用。
4.平面直角坐标系 (1)各象限内点的坐标的特点 (2)坐标轴上点的坐标的特点
(3)关于坐标轴、原点对称的点的坐标的特点
5.运动是绝对的,静止是相对的,世间上任何事物都是发展变化的.而函数就是研究两个变量之间的关系,正因为是变化的,又是数形结合,所以掌握本章知识较难,同学们在复习时要始终抓着方程(方程的解) 点的坐标 函数图象与性质这个网,综合几何代数知识,用数形结合法来解题。
6.正比例函数的定义、图象和性质:
(1)定义:形如y=kx (k为常数,k≠0)的函数叫做正比例函数。
(2)图象:一条经过原点的直线。
(3)性质: 当k>0时,y随x的增大而 ;当k<0时,y随x的增大而 。
7.一次函数的定义、图象和性质:
(1)定义:形如y=kx+b(k,b为常数,k≠0)的函数叫做一次函数
(2)图象: y=kx+b的图象是一条 ,因为两点确定一条直线,所以在画图象时,任取你喜欢的两个点,过这两点即可画出直线。
(3)性质:k的符号看直线通过一、三或二、四象限而定,b的符号看直线在y轴上的截距而定。当k>0时,y随x的增大而 ;当k<0时,y随x的增大而 。
8.反比例函数:
(1)定义:形如y=(k为常数,k≠0)叫做反比例函数。自变量x≠0,函数与x轴、y轴无交点。
(2)图象:双曲线,在用描点法画反比例函数y=的图象时,应注意自变量x的取值不能为0,应从1或-1开始对称取点.
(3)性质:当k>0时,图象位于________象限,在每一个象限内,y随x的增大而________:
当k<0时,图象位于________象限,在每一个象限内,y随x的增大而________。
(4)两支曲线无限接近与坐标轴但永远不会与坐标轴相交。
9. 反比例函数的图象和性质
k的符号 k>0 k<0
图像的大致位置
经过象限 第 象限 第 象限
性质 在每一象限内,y随x的增大而 在每一象限内,y随x的增大而
10.的几何含义:反比例函数y= (k≠0)中比例系数k的几何意义,即过双曲线y= (k≠0)上任意一点P作x轴、y轴垂线,设垂足分别为A、B,则所得矩形OAPB的面积=
【典型例题分析】
1. (2010湖北孝感,7,3分)一艘轮船在长江航线上往返于甲、乙两地.若轮船在静水中的速度不变,轮船先从甲地顺水航行到乙地,停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用的时间为t(小时),航行的路程为s(千米),则s与t的函数图象大致是( )
【答案】B
2.(2010年浙江省东阳县)汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程看作时间的函数,其图像可能是( )
A B C D
3.已知一次函数的图像经过原点,则k的值为 ( )
(A)1; (B)-1; (C)0; (D).
4. (2011广东清远,9,3分)一次函数的图象大致是( )
【答案】A
5. (2011广东广州市)当实数x的取值使得有意义时,函数y=4x+1中y的取值范围是( ).
A.y≥-7 B.y≥9 C.y>9 D.y≤9 【答案】B
6. (2011山东日照,9,4分)在平面直角坐标系中,已知直线y=-x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )
(A)(0,) (B)(0,) (C)(0,3) (D)(0,4)
【答案】B
7.(2010深圳).升旗时,旗子的高度h(米)与时间t(分)的函数图像大致为( )
8. (2011贵州遵义 )若一次函数的函数值随的增大而减小,则的取值范围是
A. B. C. D. 【答案】D
9. (2011山东泰安,13 ,3分)已知一次函数y=mx+n-2的图像如图所示,则m、n的取值范围是( )
A.m>0,n<2 B. m>0,n>2
C. m<0,n<2 D. m<0,n>2
【答案】D
10. ( 2011重庆江津, 4,4分)直线y=x-1的图像经过象限是( )
A.第一、二、三象限 B.第一、二、四象限
C.第二、三、四象限 D.第一、三、四象限
11. (2011浙江杭州 )一个矩形被直线分成面积为x,y的两部分,则y与x之间的函数关系只可能是
【答案】A
12. (2011浙江省,9,3分)如图,在平面直角坐标系中,线段AB的端点坐标为A(-2,4),B(4,2),直线y=kx-2与线段AB有交点,则k的值不可能是( )
A.-5 B.-2 C.3 D. 5
13. (2011江西 )已知一次函数y=x+b的图像经过一、二、三象限,则b的值可以是( ).
A.-2 B.-1 C.0 D.2 【答案】D
14. (2011江苏苏州,10,3分)如图,已知A点坐标为(5,0),直线y=x+b(b>0)与
y轴交于点B,连接AB,∠α=75°,则b的值为( )
A.3 B. C.4 D.
【答案】B
15. (2011山东枣庄,10,3分)如图所示,函数和的图象相交于(-1,1),
(2,2)两点.当时,x的取值范围是( )
A.x<-1 B.—1<x<2 C.x>2 D. x<-1或x>2
【答案】D
16.(2007浙江金华)一次函数与的图象如图,则下列结论
①;②;③当时,中,正确的个数是( )
A.0 B.1 C.2 D.3
17. (2011安徽芜湖,7,4分)已知直线经过
点和,则的值为( ).
A. B. C. D. 【答案】B
18. (2011四川内江,10,3分)小高从家骑自行车去学校上学,先走上坡路到达点A,再走下坡路到达点B,最后走平路到达学校,所用的时间与路程的关系如图所示。放学后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上学时一致,那么他从学校到家需要的时间是
A.14分钟 B.17分钟 C.18分钟 D.20分钟
【答案】D
19. (2011江苏连云港,4,3分)关于反比例函数的图象,
下列说法正确的是( )
A.必经过点(1,1) B.两个分支分布在第二、四象限
C.两个分支关于x轴成轴对称 D.两个分支关于原点成中心对称
【答案】D
20. (2011甘肃兰州,15,4分)如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数的图象上。若点A的坐标为(-2,-2),则k的值为( )
A.1 B.-3 C.4 D.1或-3
【答案】D
21.(2010年山东省青岛市)函数与(a≠0)
在同一直角坐标系中的图象可能是( ).
A. B. C. D.
22.(2010年安徽省芜湖市)二次函数y=ax2+bx+c的图象如图所示,反比例函数y= 与正比例函数y=(b+c)x在同一坐标系中的大致图象可能是( )
A. B. C. D.
23.(2010年四川省眉山)如图,已知双曲线经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(,4),则△AOC的面积为( )
A.12 B.9 C.6 D.4
24.(2010年宁德市)反比例函数(x>0)的图象如图所示,随着x值的增大,y值( ).
A.减小 B.增大 C.不变 D.先减小后不变
【答案】A
25. (2010年兰州市) 已知点(-1,),(2,),(3,)在
反比例函数的图像上. 下列结论中正确的是( )
A. B. C. D.
26.(2009湖南岳阳)在下图中,反比例函数的图象大致是( )
27.(2009福建龙岩)函数与在同一坐标系内的图象可以是( )
28. (2011湖南怀化,5,3分)函数与函数在同一坐标系中的大致图像是( )
【答案】D
29.(2010深圳)如图2,点P(3a,a)是反比例函y=(k>0)与⊙O的
一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
A.y= B.y= C.y= D.y=
30.(2011深圳)如图7,△ABC的内心在y轴上,点C的坐标为(2,0),点B的坐标
为(0,2),直线AC的解析式为:,则tanA的值是_________。
31.(09深圳)如图,反比例函数的图象与直线的交点
为A,B,过点A作y轴的平行线与过点B作x轴的平
行线相交于点C,则的面积为( )
A.8 B.6 C.4 D.2
32.(08深圳).如图3,直线OA与反比例函数的图象在第一象限交于A点,AB⊥x轴于点B,△OAB的面积为2,则k=
33. (2011湖北黄石,3,3分)若双曲线y=的图象
经过第二、四象限,则k的取值范围是( )
A.k> B. k< C. k= D. 不存在 【答案】B
34. (2011山东威海,5,3分)下列各点中,在函数图象上的是( )
A.(-2,-4) B.(2,3) C.(-1,6) D.
【答案】C
35. (2011浙江台州)如图,反比例函数的图象与一次函数的图象交于点M,N,已点M的坐标为(1,3),点N的纵坐标为-1,根据图象信息可得关于x的方程=的解为( )
A. -3,1 B. -3,3 C. -1,1 D.3,-1
【答案】A
36. ( 2011重庆江津, 6,4分)已知如图,A是反比例函数的图像上的一点,
AB⊥x轴于点B,且△ABO的面积是3,则k的值是( )
A.3 B.-3 C.6 D.-6 【答案】C
37. (2011湖北黄冈,4,3分)如图:点A在双曲线上,AB⊥x
轴于B,且△AOB的面积S△AOB=2,则k=______.
38. (2011浙江衢州)在直角坐标系中,有如图所示的轴于点,斜边,反比例函数的图像经过的中点,且与交于点,则点的坐标为 . 【答案】
39. (2011广东株洲)如图,直线l过A、B两点,
A(,),B(,),则直线l的解析式为 .
【答案】y=x-1
40.(2011四川成都,21,4分)在平面直角坐标系中,点P(2,)在正比例函数的图象上,则点Q()位于第______象限. 【答案】四.
41. (2011湖南怀化,12,3分)一次函数y=-2x+3中,y的值随x值增大而___________.(填“增大”或“减小”) 【答案】减小
42. (2011山东日照,22,9分)某商业集团新进了40台空调机,60台电冰箱,计划调配给下属的甲、乙两个连锁店销售,其中70台给甲连锁店,30台给乙连锁店.两个连锁店销售这两种电器每台的利润(元)如下表:
空调机 电冰箱
甲连锁店 200 170
乙连锁店 160 150
设集团调配给甲连锁店x台空调机,集团卖出这100台电器的总利润为y(元).
(1)求y关于x的函数关系式,并求出x的取值范围;
(2)为了促销,集团决定仅对甲连锁店的空调机每台让利a元销售,其他的销售利润不变,并且让利后每台空调机的利润仍然高于甲连锁店销售的每台电冰箱的利润,问该集团应该如何设计调配方案,使总利润达到最大?
【答案】 (1)根据题意知,调配给甲连锁店电冰箱(70-x)台,
调配给乙连锁店空调机(40-x)台,电冰箱(x-10)台, 则y=200x+170(70-x)+160(40-x)+150(x-10),
即y=20x+16800.∵
∴10≤x≤40. ∴y=20x+168009 (10≤x≤40);
(2)按题意知:y=(200-a)x+170(70-x)+160(40-x)+150(x-10),
即y=(20-a)x+16800. ∵200-a>170,∴a<30.
当0<a<20时,x=40,即调配给甲连锁店空调机40台,电冰箱30台,乙连锁店空调0台,
电冰箱30台; 当a=20时,x的取值在10≤x≤40内的所有方案利润相同;
当20<a<30时,x=10,即调配给甲连锁店空调机10台,电冰箱60台,乙连锁店空调30台,电冰箱0台;
43. (2011湖北宜昌,19,7分)某市实施“限塑令”后,2008年大约减少塑料消耗约4万吨.调查分析结果显示,从2008年开始,五年内该市因实施“限塑令”而减少的塑料消耗量y(万吨)随着时间(年)逐年成直线上升,y与之间的关系如图所示.
(1)求y与之间的关系式;
(2)请你估计,该市2011年因实施“限塑令”而减少的塑料消耗量为多少
(第43题图)
【答案】解:(1)设y=kx+b. (1分)由题意,得2008k+b=4,(2分)2010k+b=6,(3分).
解得k=1(4分)b=-2004(5分)∴y=x-2004.(2)当x=2011时,y=2011-2004(6分)=7.(7分)∴该市2011年因“限塑令”而减少的塑料消耗量约为7万吨.
o
y
x
y
x
o
t
h
O
t
h
O
t
h
O
t
h
O
A
B
C
D
(-1,1)
(2,2)
x
y
O
x
y
O
3
第16题
400
0
5
9
17
1200
2000
s(米)
t(分钟)
x
y
O
A
B
C
D
y
x
O
y
x
O
x
y
O
x
O
y
x
y
O
第24题图
x
y
O
A.
x
y
O
B.
x
y
O
C.
x
y
O
D.
x
O
y
P
图2
A
B
C
30题
x
y
O
A
O
B
C
y
o
A
B
x
第36题图
A
B
O
x
y
第37题图
(第38题)
同课章节目录
