2020-2021学年山东省烟台市招远市七年级(下)期中数学试卷(五四学制)(word版无答案)
文档属性
| 名称 | 2020-2021学年山东省烟台市招远市七年级(下)期中数学试卷(五四学制)(word版无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 167.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-23 19:42:43 | ||
图片预览


文档简介
2020-2021学年山东省烟台市招远市七年级(下)期中数学试卷(五四学制)
一.选择题(本大题共12个小题,每小题3分,满分36分)
1.下列成语描述的事件为随机事件的是( )
A.缘木求鱼 B.水落石出 C.瓮中捉鳖 D.守株待兔
2.给出下列命题:
(1)三角形的一个外角一定大于它的一个内角
(2)若一个三角形的三个内角之比为1:3:4,它肯定是直角三角形
(3)三角形的最小内角不能大于60°
(4)三角形的一个外角等于和它不相邻的两个内角的和
其中真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
3.用加减法解方程组时,下列变形正确的是( )
A. B.
C. D.
4.下列说法正确的是( )
A.篮球队员在罚球线上投篮一次,则“投中”是随机事件
B.明天的降水概率为40%,则“明天下雨”是确定事件
C.任意抛掷一枚质地均匀的硬币10次,则“5次正面朝上”是必然事件
D.a是实数,则“|a|≥0”是不可能事件
5.如图,在证明“△ABC内角和等于180°”时,延长BC至D,过点C作CE∥AB,得到∠ABC=∠ECD,∠BAC=∠ACE,由于∠BCD=180°,可得到∠ABC+∠ACB+∠BAC=180°,这个证明方法体现的数学思想是( )
A.数形结合 B.特殊到一般 C.一般到特殊 D.转化
6.若方程组的解满足x+y=2021,则k等于( )
A.2019 B.2020 C.2021 D.2022
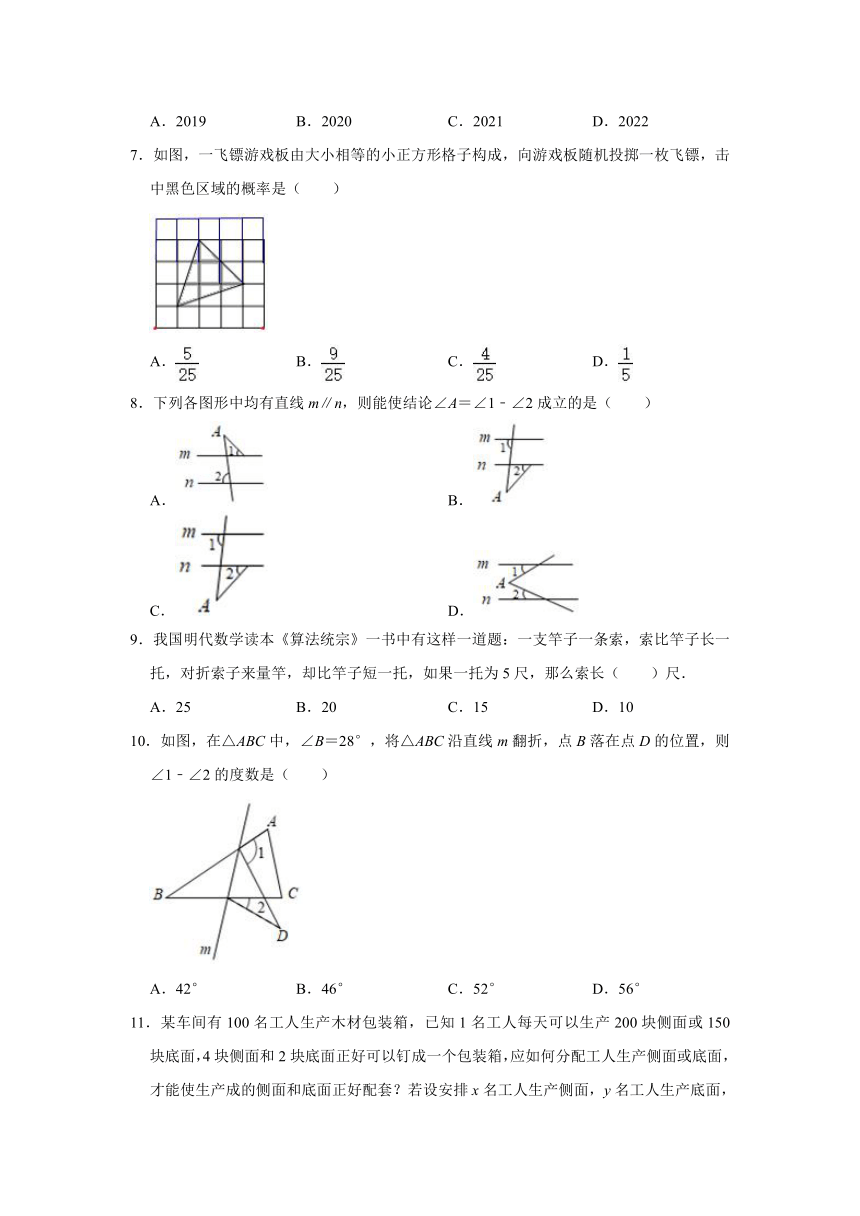
7.如图,一飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中黑色区域的概率是( )
A. B. C. D.
8.下列各图形中均有直线m∥n,则能使结论∠A=∠1﹣∠2成立的是( )
A. B.
C. D.
9.我国明代数学读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托,如果一托为5尺,那么索长( )尺.
A.25 B.20 C.15 D.10
10.如图,在△ABC中,∠B=28°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1﹣∠2的度数是( )
A.42° B.46° C.52° D.56°
11.某车间有100名工人生产木材包装箱,已知1名工人每天可以生产200块侧面或150块底面,4块侧面和2块底面正好可以钉成一个包装箱,应如何分配工人生产侧面或底面,才能使生产成的侧面和底面正好配套?若设安排x名工人生产侧面,y名工人生产底面,则可列方程组( )
A. B.
C. D.
12.如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°﹣∠ABD;④∠BDC=∠BAC.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(本大题共6个小题,每小题3分,满分18分)
13.小东认为:任意抛掷一个啤酒盖,啤酒盖落地后印有商标一面向上的可能性的大小是,你认为小东的想法 (“合理”或“不合理”)
14.如图,将一副三角板如图摆放,则图中∠1的度数是 度.
15.如图,在同一直角坐标系中作出一次函数y=k1x与y=k2x+b的图象,则二元一次方程组的解是 .
16.如图,直线l1∥l2,点A在l1上,以点A为圆心,适当长为半径画弧,分别交直线l1,l2于B,C两点;连接AC,BC.若∠ABC=65°,则∠1的大小为 .
17.定义一种新运算“※”,规定x※y=ax+by2,其中a、b为常数,且﹣1※1=0,2※1=3,则2※5= .
18.如图,△ABC与△CDE都是等边三角形,且∠EBD=75°,则∠AEB的度数是 .
三.解答题(第19、20、21题各8分,第22、23、24题各10分,第25题各12分)
19.解方程:
(1).
(2)
20.一次抽奖活动设置如下的翻奖牌,翻奖牌的正面、背面如下,如果你只能在9个数字中选中一个翻牌,请解决下面的问题:
(1)直接写出抽到“手机”奖品的可能性的大小;
(2)每个奖牌只能翻一次,翻过的奖牌不能再翻.若第一次没有抽到“手机”奖品,请求出第二次抽到“手机”奖品的可能性的大小;
(3)请你根据题意设计翻奖牌反面的奖品,包含(手机、微波炉、球拍、电影票,谢谢参与)使得最后抽到“球拍”的可能性大小是.
21.如图,△ABC中,CD⊥AB于点D,DE∥BC交AC于点E,EF⊥CD于点G,交BC于点F.
(1)求证:∠ADE=∠EFC;
(2)若∠ACB=78°,∠A=60°,求∠DCB的度数.
22.如图,过点A(0,2),B(3,0)的直线AB与直线CD:y=x﹣4交于D,C为直线CD与y轴的交点,求:
(1)直线AB对应的函数表达式;
(2)求S△ADC.
23.金都百货电器商场销售进价分别为120元、190元的A、B两种型号的电风扇,第一批货两周销售完毕,如下表所示是近二周的销售情况(进价、售价均保持不变,利润=销售收入﹣进货成本):
销售时段 销售数量 销售收入
A种型号 B种型号
第一周 5 7 2570
第二周 8 9 3540
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场再购进这两种型号的电风扇共120台,并且全部销售完,该商场能否实现这两批电风扇的总利润为8310元的目标?若能,请给出相应的采购方案:若不能,请说明理由.
24.三角形ABC中,D是AB上一点,DE∥BC交AC于点E,点F是线段DE延长线上一点,连接FC,∠BCF+∠ADE=180°.
(1)如图2,连接BE,若∠ABE=40°,∠ACF=60°,求∠BEC的度数;
(2)如图3,在(2)的条件下,点G是线段FC延长线上一点,若∠EBC:∠ECB=3:5,BE平分∠ABG,求∠CBG的度数.
25.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发,驶向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地时,求货车与甲地的距离;
(2)求线段CD对应的函数表达式;
(3)在轿车行进过程,轿车行驶多少时间,两车相距15千米.
一.选择题(本大题共12个小题,每小题3分,满分36分)
1.下列成语描述的事件为随机事件的是( )
A.缘木求鱼 B.水落石出 C.瓮中捉鳖 D.守株待兔
2.给出下列命题:
(1)三角形的一个外角一定大于它的一个内角
(2)若一个三角形的三个内角之比为1:3:4,它肯定是直角三角形
(3)三角形的最小内角不能大于60°
(4)三角形的一个外角等于和它不相邻的两个内角的和
其中真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
3.用加减法解方程组时,下列变形正确的是( )
A. B.
C. D.
4.下列说法正确的是( )
A.篮球队员在罚球线上投篮一次,则“投中”是随机事件
B.明天的降水概率为40%,则“明天下雨”是确定事件
C.任意抛掷一枚质地均匀的硬币10次,则“5次正面朝上”是必然事件
D.a是实数,则“|a|≥0”是不可能事件
5.如图,在证明“△ABC内角和等于180°”时,延长BC至D,过点C作CE∥AB,得到∠ABC=∠ECD,∠BAC=∠ACE,由于∠BCD=180°,可得到∠ABC+∠ACB+∠BAC=180°,这个证明方法体现的数学思想是( )
A.数形结合 B.特殊到一般 C.一般到特殊 D.转化
6.若方程组的解满足x+y=2021,则k等于( )
A.2019 B.2020 C.2021 D.2022
7.如图,一飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中黑色区域的概率是( )
A. B. C. D.
8.下列各图形中均有直线m∥n,则能使结论∠A=∠1﹣∠2成立的是( )
A. B.
C. D.
9.我国明代数学读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托,如果一托为5尺,那么索长( )尺.
A.25 B.20 C.15 D.10
10.如图,在△ABC中,∠B=28°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1﹣∠2的度数是( )
A.42° B.46° C.52° D.56°
11.某车间有100名工人生产木材包装箱,已知1名工人每天可以生产200块侧面或150块底面,4块侧面和2块底面正好可以钉成一个包装箱,应如何分配工人生产侧面或底面,才能使生产成的侧面和底面正好配套?若设安排x名工人生产侧面,y名工人生产底面,则可列方程组( )
A. B.
C. D.
12.如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°﹣∠ABD;④∠BDC=∠BAC.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(本大题共6个小题,每小题3分,满分18分)
13.小东认为:任意抛掷一个啤酒盖,啤酒盖落地后印有商标一面向上的可能性的大小是,你认为小东的想法 (“合理”或“不合理”)
14.如图,将一副三角板如图摆放,则图中∠1的度数是 度.
15.如图,在同一直角坐标系中作出一次函数y=k1x与y=k2x+b的图象,则二元一次方程组的解是 .
16.如图,直线l1∥l2,点A在l1上,以点A为圆心,适当长为半径画弧,分别交直线l1,l2于B,C两点;连接AC,BC.若∠ABC=65°,则∠1的大小为 .
17.定义一种新运算“※”,规定x※y=ax+by2,其中a、b为常数,且﹣1※1=0,2※1=3,则2※5= .
18.如图,△ABC与△CDE都是等边三角形,且∠EBD=75°,则∠AEB的度数是 .
三.解答题(第19、20、21题各8分,第22、23、24题各10分,第25题各12分)
19.解方程:
(1).
(2)
20.一次抽奖活动设置如下的翻奖牌,翻奖牌的正面、背面如下,如果你只能在9个数字中选中一个翻牌,请解决下面的问题:
(1)直接写出抽到“手机”奖品的可能性的大小;
(2)每个奖牌只能翻一次,翻过的奖牌不能再翻.若第一次没有抽到“手机”奖品,请求出第二次抽到“手机”奖品的可能性的大小;
(3)请你根据题意设计翻奖牌反面的奖品,包含(手机、微波炉、球拍、电影票,谢谢参与)使得最后抽到“球拍”的可能性大小是.
21.如图,△ABC中,CD⊥AB于点D,DE∥BC交AC于点E,EF⊥CD于点G,交BC于点F.
(1)求证:∠ADE=∠EFC;
(2)若∠ACB=78°,∠A=60°,求∠DCB的度数.
22.如图,过点A(0,2),B(3,0)的直线AB与直线CD:y=x﹣4交于D,C为直线CD与y轴的交点,求:
(1)直线AB对应的函数表达式;
(2)求S△ADC.
23.金都百货电器商场销售进价分别为120元、190元的A、B两种型号的电风扇,第一批货两周销售完毕,如下表所示是近二周的销售情况(进价、售价均保持不变,利润=销售收入﹣进货成本):
销售时段 销售数量 销售收入
A种型号 B种型号
第一周 5 7 2570
第二周 8 9 3540
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场再购进这两种型号的电风扇共120台,并且全部销售完,该商场能否实现这两批电风扇的总利润为8310元的目标?若能,请给出相应的采购方案:若不能,请说明理由.
24.三角形ABC中,D是AB上一点,DE∥BC交AC于点E,点F是线段DE延长线上一点,连接FC,∠BCF+∠ADE=180°.
(1)如图2,连接BE,若∠ABE=40°,∠ACF=60°,求∠BEC的度数;
(2)如图3,在(2)的条件下,点G是线段FC延长线上一点,若∠EBC:∠ECB=3:5,BE平分∠ABG,求∠CBG的度数.
25.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发,驶向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地时,求货车与甲地的距离;
(2)求线段CD对应的函数表达式;
(3)在轿车行进过程,轿车行驶多少时间,两车相距15千米.
同课章节目录
