18.2.2.2菱形的判定-2020-2021学年人教版八年级数学下册导学案(表格式 含答案)
文档属性
| 名称 | 18.2.2.2菱形的判定-2020-2021学年人教版八年级数学下册导学案(表格式 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 116.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 00:00:00 | ||
图片预览

文档简介
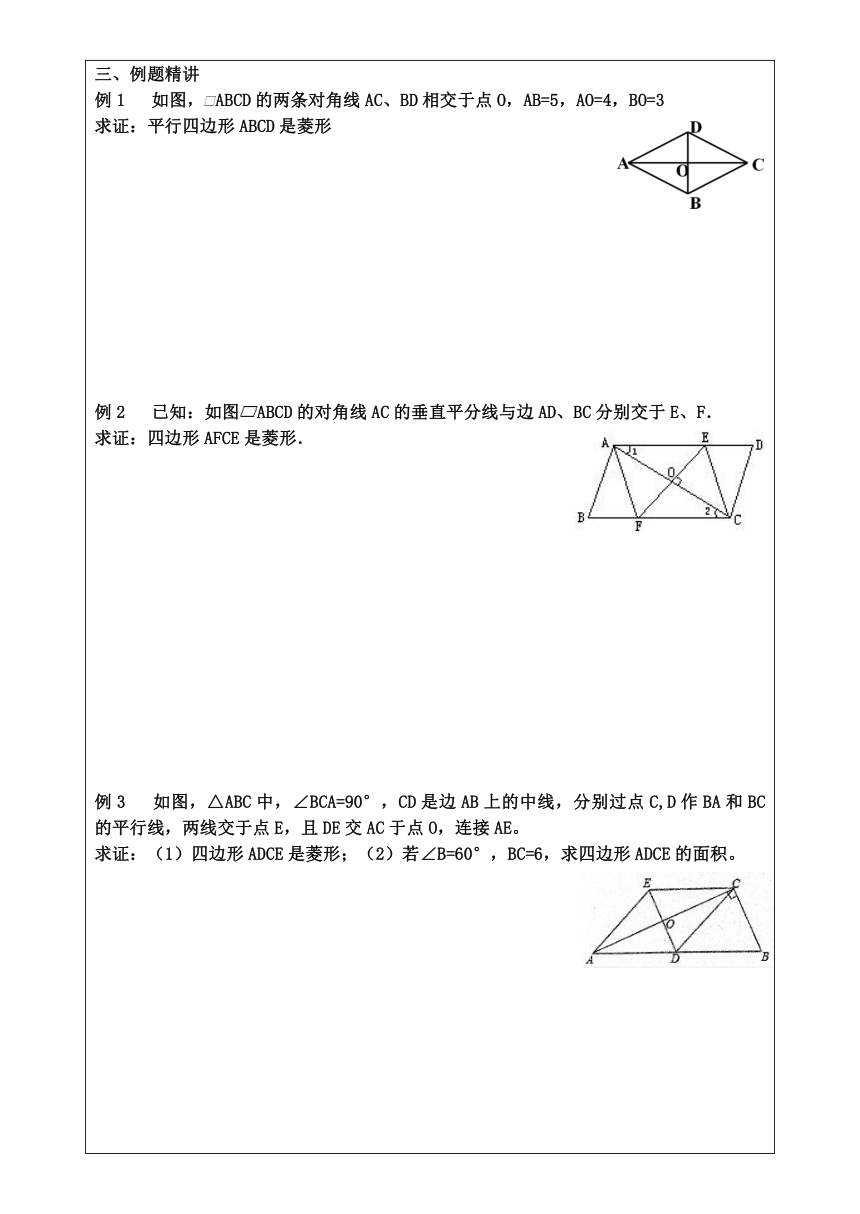
授课人 年级 八 学科 数学 授课时间
课题 18.2.2.1菱形的判定 课型 新授
学习 目标 1.理解并掌握菱形的判定方法.
2.使学生能应用菱形定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力
学习 关键 重点 菱形的判定
难点 菱形的判定及性质的综合应用
学教过程
创设情境独立思考 阅读课本P57 ~58 页,思考下列问题:
(1)什么是菱形?
菱形有哪些性质?
边:
角:
对角线:
菱形的判定方法有几种?
边:
归纳:
④
⑤
对角线:
巩固练习
1.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形 D.当AC=BD时,它是菱形
2.下列命题中正确的是( )
A.对角线互相平分的四边形是菱形 B.对角线互相平分且相等的四边形是菱形
C.对角线互相垂直的四边形是菱形 D.对角线互相垂直且平分的四边形是菱形
3.在?ABCD中,若添加一个条件 ,则四边形ABCD是矩形;
若添加一个条件 ,则四边形ABCD是菱形.
三、例题精讲
例1 如图,ABCD的两条对角线AC、BD相交于点O,AB=5,AO=4,BO=3
求证:平行四边形ABCD是菱形
例2 已知:如图ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.
求证:四边形AFCE是菱形.
例3 如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE。
求证:(1)四边形ADCE是菱形;(2)若∠B=60°,BC=6,求四边形ADCE的面积。
四、达标检测
1、(4分)
(1)对角线互相平分的四边形是 ;
(2)对角线互相垂直平分的四边形是_____________;
(3)对角线相等且互相平分的四边形是_____________;
(4)两组对边分别平行,且对角线 的四边形是菱形.
2、(4分) ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形;
(2)若AC=BD,则□ABCD是 形;
(3)若∠ABC是直角,则□ABCD是 形;
(4)若∠BAO=∠DAO,则□ABCD是 形。
3、(4分)能判定一个四边形是菱形的条件是( )
A.对角线相等且互相垂直 B.对角线相等且互相平分
C.对角线互相垂直 D.对角线互相垂直平分
4、(8分)如图,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD,DE和CE相交于E,
求证:四边形OCED是菱形。
答案:
二、D D AC=BD;AC⊥BD
三、例1 证明:∵AB=5,AO=4,BO=3
∴AB2=AO2+BO2, ∴△AOB是直角三角形 ∴AC⊥BD ∴平行四边形ABCD是菱形
例2、证明:∵四边形ABCD是平行四边形,
∴AE∥FC.
∴∠1=∠2.
又∠AOE=∠COF,AO=CO,
∴△AOE≌△COF.
∴EO=FO.
∴四边形AFCE是平行四边形.
又EF⊥AC,
∴AFCE是菱形(对角线互相垂直的平行四边形是菱形).
例3、(1)证明:∵DE∥BC,CE∥BA, ∴四边形BCED是平行四边形. ∴CE=BD
∵∠BCA=90°,CD是边AB上的中线 ∴CD=AD=BD ∴CE=AD
∵CE∥AD ∴四边形ADCE是平行四边形 ∵CD=AD ∴四边形ADCE是菱形
∵CD=BD,∠B=60° ∴∠DCB=∠B=60° ∴△BCD是等边三角形 ∴CD=BC=6
∵∠BCA=90° ∴∠DCO=30° ∵四边形ADCE是菱形 ∴∠DOC=90°,OA=OC,OE=OD
∴OD=CD=3,OC=3 ∴S=×3×3×4=18
四、1.平行四边形、菱形、矩形、互相垂直 2.菱形、矩形、矩形、菱形 3.D
4.证明:∵DE∥AC,CE∥BD ∴四边形OCED是平行四边形
∵四边形ABCD是矩形 ∴OA=OC,OB=OD,AC=BD ∴OC=OD ∴四边形OCED是菱形
课题 18.2.2.1菱形的判定 课型 新授
学习 目标 1.理解并掌握菱形的判定方法.
2.使学生能应用菱形定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力
学习 关键 重点 菱形的判定
难点 菱形的判定及性质的综合应用
学教过程
创设情境独立思考 阅读课本P57 ~58 页,思考下列问题:
(1)什么是菱形?
菱形有哪些性质?
边:
角:
对角线:
菱形的判定方法有几种?
边:
归纳:
④
⑤
对角线:
巩固练习
1.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形 D.当AC=BD时,它是菱形
2.下列命题中正确的是( )
A.对角线互相平分的四边形是菱形 B.对角线互相平分且相等的四边形是菱形
C.对角线互相垂直的四边形是菱形 D.对角线互相垂直且平分的四边形是菱形
3.在?ABCD中,若添加一个条件 ,则四边形ABCD是矩形;
若添加一个条件 ,则四边形ABCD是菱形.
三、例题精讲
例1 如图,ABCD的两条对角线AC、BD相交于点O,AB=5,AO=4,BO=3
求证:平行四边形ABCD是菱形
例2 已知:如图ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.
求证:四边形AFCE是菱形.
例3 如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE。
求证:(1)四边形ADCE是菱形;(2)若∠B=60°,BC=6,求四边形ADCE的面积。
四、达标检测
1、(4分)
(1)对角线互相平分的四边形是 ;
(2)对角线互相垂直平分的四边形是_____________;
(3)对角线相等且互相平分的四边形是_____________;
(4)两组对边分别平行,且对角线 的四边形是菱形.
2、(4分) ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形;
(2)若AC=BD,则□ABCD是 形;
(3)若∠ABC是直角,则□ABCD是 形;
(4)若∠BAO=∠DAO,则□ABCD是 形。
3、(4分)能判定一个四边形是菱形的条件是( )
A.对角线相等且互相垂直 B.对角线相等且互相平分
C.对角线互相垂直 D.对角线互相垂直平分
4、(8分)如图,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD,DE和CE相交于E,
求证:四边形OCED是菱形。
答案:
二、D D AC=BD;AC⊥BD
三、例1 证明:∵AB=5,AO=4,BO=3
∴AB2=AO2+BO2, ∴△AOB是直角三角形 ∴AC⊥BD ∴平行四边形ABCD是菱形
例2、证明:∵四边形ABCD是平行四边形,
∴AE∥FC.
∴∠1=∠2.
又∠AOE=∠COF,AO=CO,
∴△AOE≌△COF.
∴EO=FO.
∴四边形AFCE是平行四边形.
又EF⊥AC,
∴AFCE是菱形(对角线互相垂直的平行四边形是菱形).
例3、(1)证明:∵DE∥BC,CE∥BA, ∴四边形BCED是平行四边形. ∴CE=BD
∵∠BCA=90°,CD是边AB上的中线 ∴CD=AD=BD ∴CE=AD
∵CE∥AD ∴四边形ADCE是平行四边形 ∵CD=AD ∴四边形ADCE是菱形
∵CD=BD,∠B=60° ∴∠DCB=∠B=60° ∴△BCD是等边三角形 ∴CD=BC=6
∵∠BCA=90° ∴∠DCO=30° ∵四边形ADCE是菱形 ∴∠DOC=90°,OA=OC,OE=OD
∴OD=CD=3,OC=3 ∴S=×3×3×4=18
四、1.平行四边形、菱形、矩形、互相垂直 2.菱形、矩形、矩形、菱形 3.D
4.证明:∵DE∥AC,CE∥BD ∴四边形OCED是平行四边形
∵四边形ABCD是矩形 ∴OA=OC,OB=OD,AC=BD ∴OC=OD ∴四边形OCED是菱形
