18.2.1.2矩形的判定-2020-2021学年人教版八年级数学下册导学案(Word版含答案)
文档属性
| 名称 | 18.2.1.2矩形的判定-2020-2021学年人教版八年级数学下册导学案(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 83.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 00:00:00 | ||
图片预览


文档简介
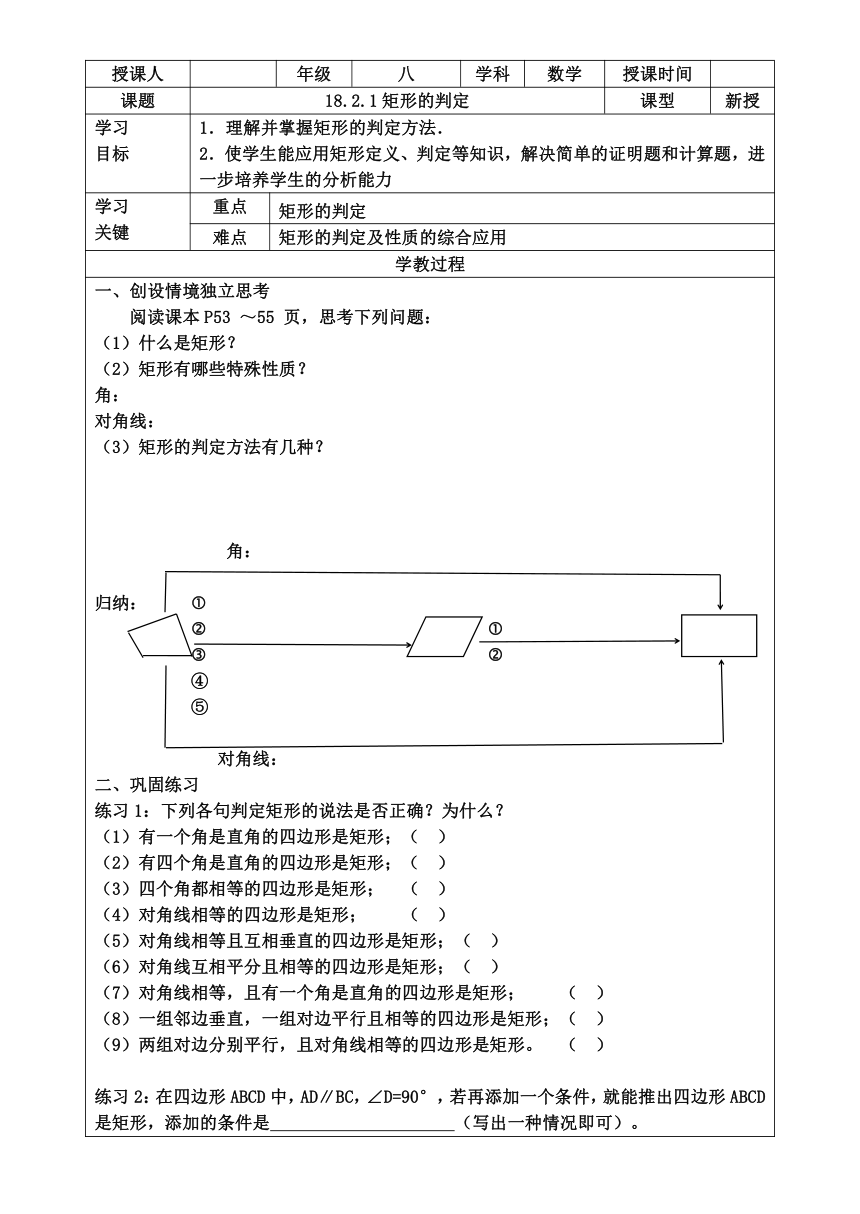
授课人 年级 八 学科 数学 授课时间
课题 18.2.1矩形的判定 课型 新授
学习 目标 1.理解并掌握矩形的判定方法.
2.使学生能应用矩形定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力
学习 关键 重点 矩形的判定
难点 矩形的判定及性质的综合应用
学教过程
创设情境独立思考 阅读课本P53 ~55 页,思考下列问题:
(1)什么是矩形?
矩形有哪些特殊性质?
角:
对角线:
矩形的判定方法有几种?
角:
归纳:
④
⑤
对角线:
二、巩固练习
练习1:下列各句判定矩形的说法是否正确?为什么?
(1)有一个角是直角的四边形是矩形;( )
(2)有四个角是直角的四边形是矩形;( )
(3)四个角都相等的四边形是矩形; ( )
(4)对角线相等的四边形是矩形; ( )
(5)对角线相等且互相垂直的四边形是矩形;( )
(6)对角线互相平分且相等的四边形是矩形;( )
(7)对角线相等,且有一个角是直角的四边形是矩形; ( )
(8)一组邻边垂直,一组对边平行且相等的四边形是矩形;( )
(9)两组对边分别平行,且对角线相等的四边形是矩形。 ( )
练习2:在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,就能推出四边形ABCD是矩形,添加的条件是 (写出一种情况即可)。
三、例题精讲
例1 如图,在△ABC中,AB=AC,AD是BC边上的中线,四边形ADBE是平行四边形,
求证:四边形ADBE是矩形。
例2:已知:在ABCD中,对角线AC、BD相交于点O,∠1=∠2,求证:ABCD是矩形
例3:已知 ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4 cm,求这个平行四边形的面积.
分析:首先根据△AOB是等边三角形及平行四边形对角线互相平分的性质判定出ABCD是矩形,再利用勾股定理计算边长,从而得到面积值.
四、达标检测
1、(4分)工人师傅做铝合金窗框分下面三个步骤进行:
⑴ 先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH;
⑵ 摆放成如图②的四边形,则这时窗框的形状是 形,根据的数学道理是: ;
⑶ 将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是 形,根据的数学道理是: ;
2、(4分)下列说法正确的是( ).
(A)有一组对角是直角的四边形一定是矩形
(B)有一组邻角是直角的四边形一定是矩形
(C)对角线互相平分的四边形是矩形
(D)对角互补的平行四边形是矩形
3、(8分)已知,平行四边形ABCD中,AB=5,AD=12,BD=13.求证:平行四边形ABCD是矩形。
选做题:(8分)已知:在△ABC中,∠ACB=90°,CD为中线,延长CD到点E,使得
DE=CD.连结AE,BE,求证:四边形ACBE为矩形.
答案:
二、1、× √ √ × × √ × √ √
∠A=90°或AD=BC或AB∥CD
三、例1、证明:∵AB=AC,AD是BC边上的中线
∴AD⊥BC
∴∠ADB=90°
∵四边形ADBE是平行四边形
∴四边形ADBE是矩形
证明:∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
∵∠1=∠2
∴OA=OB
∴OA=OB=OC=OD,即AC=BD
∴ABCD是矩形
解:∵四边形ABCD是平行四边形,
∴AO=AC,BO=BD.
∵AO=BO,∴AC=BD.
∴ABCD是矩形(对角线相等的平行四边形是矩形).
在Rt△ABC中,∵AB=4cm,AC=2AO=8cm,∴BC=(cm).
四、1、平行四边形,两组对边分别相等的四边形是平行四边形;矩形,有一个角是直角的平行四边形是矩形。
2、D
3、证明:在△ABD中,∵AB2+AD2=52+122=169 ,BD2=132=169
∴AB2+AD2=BD2
∴∠A=90°
∵四边形ABCD是平行四边形
∴平行四边形ABCD是矩形。
选做题:证明:∵∠ACB=90°,CD为中线
∴CD=AD=BD=AB
∵DE=CD
∴四边形ACBE为平行四边形,DE=CD=AD=BD
∴AB=CE
∴四边形ACBE为矩形
课题 18.2.1矩形的判定 课型 新授
学习 目标 1.理解并掌握矩形的判定方法.
2.使学生能应用矩形定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力
学习 关键 重点 矩形的判定
难点 矩形的判定及性质的综合应用
学教过程
创设情境独立思考 阅读课本P53 ~55 页,思考下列问题:
(1)什么是矩形?
矩形有哪些特殊性质?
角:
对角线:
矩形的判定方法有几种?
角:
归纳:
④
⑤
对角线:
二、巩固练习
练习1:下列各句判定矩形的说法是否正确?为什么?
(1)有一个角是直角的四边形是矩形;( )
(2)有四个角是直角的四边形是矩形;( )
(3)四个角都相等的四边形是矩形; ( )
(4)对角线相等的四边形是矩形; ( )
(5)对角线相等且互相垂直的四边形是矩形;( )
(6)对角线互相平分且相等的四边形是矩形;( )
(7)对角线相等,且有一个角是直角的四边形是矩形; ( )
(8)一组邻边垂直,一组对边平行且相等的四边形是矩形;( )
(9)两组对边分别平行,且对角线相等的四边形是矩形。 ( )
练习2:在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,就能推出四边形ABCD是矩形,添加的条件是 (写出一种情况即可)。
三、例题精讲
例1 如图,在△ABC中,AB=AC,AD是BC边上的中线,四边形ADBE是平行四边形,
求证:四边形ADBE是矩形。
例2:已知:在ABCD中,对角线AC、BD相交于点O,∠1=∠2,求证:ABCD是矩形
例3:已知 ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4 cm,求这个平行四边形的面积.
分析:首先根据△AOB是等边三角形及平行四边形对角线互相平分的性质判定出ABCD是矩形,再利用勾股定理计算边长,从而得到面积值.
四、达标检测
1、(4分)工人师傅做铝合金窗框分下面三个步骤进行:
⑴ 先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH;
⑵ 摆放成如图②的四边形,则这时窗框的形状是 形,根据的数学道理是: ;
⑶ 将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是 形,根据的数学道理是: ;
2、(4分)下列说法正确的是( ).
(A)有一组对角是直角的四边形一定是矩形
(B)有一组邻角是直角的四边形一定是矩形
(C)对角线互相平分的四边形是矩形
(D)对角互补的平行四边形是矩形
3、(8分)已知,平行四边形ABCD中,AB=5,AD=12,BD=13.求证:平行四边形ABCD是矩形。
选做题:(8分)已知:在△ABC中,∠ACB=90°,CD为中线,延长CD到点E,使得
DE=CD.连结AE,BE,求证:四边形ACBE为矩形.
答案:
二、1、× √ √ × × √ × √ √
∠A=90°或AD=BC或AB∥CD
三、例1、证明:∵AB=AC,AD是BC边上的中线
∴AD⊥BC
∴∠ADB=90°
∵四边形ADBE是平行四边形
∴四边形ADBE是矩形
证明:∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
∵∠1=∠2
∴OA=OB
∴OA=OB=OC=OD,即AC=BD
∴ABCD是矩形
解:∵四边形ABCD是平行四边形,
∴AO=AC,BO=BD.
∵AO=BO,∴AC=BD.
∴ABCD是矩形(对角线相等的平行四边形是矩形).
在Rt△ABC中,∵AB=4cm,AC=2AO=8cm,∴BC=(cm).
四、1、平行四边形,两组对边分别相等的四边形是平行四边形;矩形,有一个角是直角的平行四边形是矩形。
2、D
3、证明:在△ABD中,∵AB2+AD2=52+122=169 ,BD2=132=169
∴AB2+AD2=BD2
∴∠A=90°
∵四边形ABCD是平行四边形
∴平行四边形ABCD是矩形。
选做题:证明:∵∠ACB=90°,CD为中线
∴CD=AD=BD=AB
∵DE=CD
∴四边形ACBE为平行四边形,DE=CD=AD=BD
∴AB=CE
∴四边形ACBE为矩形
