18.2.1.1矩形的性质-2020-2021学年人教版八年级数学下册导学案(Word版含答案)
文档属性
| 名称 | 18.2.1.1矩形的性质-2020-2021学年人教版八年级数学下册导学案(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 101.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 08:39:04 | ||
图片预览

文档简介
授课人 年级 八 学科 数学 授课时间
课题 18.2.1矩形的性质 课型 新授
学习 目标 1.掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系.
2.会初步运用矩形的概念和性质来解决有关问题.
学习 关键 重点 矩形的性质
难点 矩形的性质的灵活应用
学教过程
创设情境独立思考 1、阅读课本P52 ~53 页,思考下列问题:
(1)什么是矩形?矩形是平行四边形吗?
矩形有哪些性质?
边:
角:
对角线:
对称性:
直角三角形斜边的中线和斜边有什么关系?为什么?
二、自学检测
1.矩形具有而平行四边行不具有的的性质是( )
A、对角相等 B、对角线相等 C、对角线互相平分 D、对边平行且相等
2.已知:四边形ABCD是矩形,
(1)若已知AB=8㎝,AD=6㎝,则AC=_____ ㎝,OB=_____ ㎝
(2)若已知∠DOC=120°,AC=8㎝,则AD=____cm,AB=____cm
3.已知△ABC是Rt△,∠ABC=90°,BD是斜边AC上的中线,
(1)若BD=3㎝,则AC= ㎝
(2)若∠C=30°,AB=5㎝,则AC= ㎝,BD= ㎝
三、例题精讲
例1 已知:如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长.
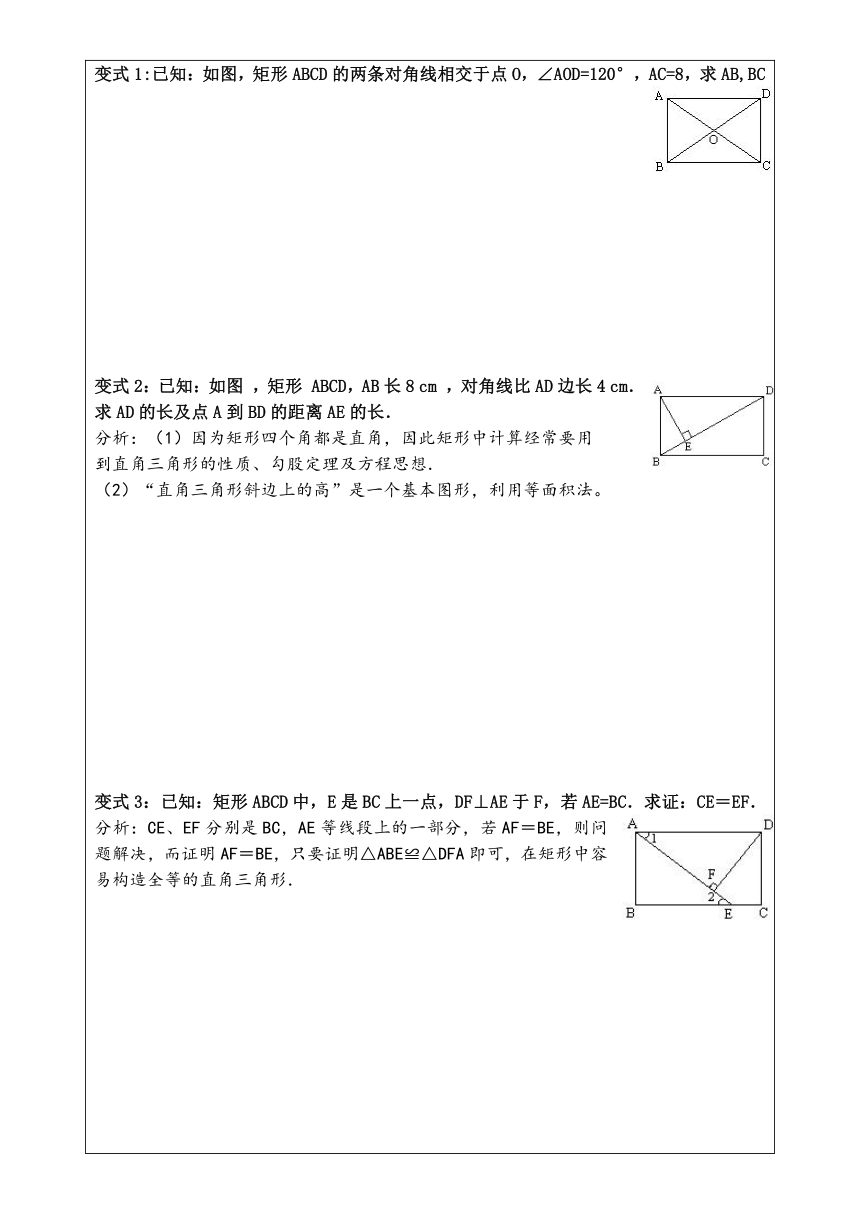
变式1:已知:如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AC=8,求AB,BC
变式2:已知:如图 ,矩形 ABCD,AB长8 cm ,对角线比AD边长4 cm.
求AD的长及点A到BD的距离AE的长.
分析:(1)因为矩形四个角都是直角,因此矩形中计算经常要用
到直角三角形的性质、勾股定理及方程思想.
“直角三角形斜边上的高”是一个基本图形,利用等面积法。
变式3:已知:矩形ABCD中,E是BC上一点,DF⊥AE于F,若AE=BC.求证:CE=EF.
分析:CE、EF分别是BC,AE等线段上的一部分,若AF=BE,则问题解决,而证明AF=BE,只要证明△ABE≌△DFA即可,在矩形中容易构造全等的直角三角形.
四、达标检测
1.(4分)矩形的两条对角线的夹角为60°,对角线长为15cm,较短边的长为( ).
(A)12cm (B)10cm (C)7.5cm (D)5cm
2.(4分)下列说法错误的是( ).
(A)矩形的对角线互相平分 (B)矩形的对角线相等
(C)有一个角是直角的四边形是矩形 (D)有一个角是直角的平行四边形叫做矩形
3.(4分)矩形的对角线把矩形分成的三角形中全等三角形一共有( ).
(A)2对 (B)4对 (C)6对 (D)8对
4.(4分)(1)已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为 、 、 、 .
(2)已知矩形的一条对角线长为10cm,两条对角线的一个交角为120°,则矩形的边长分别为 cm, cm, cm, cm.
5.(8分)如图,矩形ABCD中,AB=2BC,且AB=AE,求∠CBE的度数.
选做题:(8分)已知:矩形ABCD中,BC=2AB,E是BC的中点,求证:EA⊥ED.
答案:
二、1、B 2、(1)10,5;(2)4, 3、(1)6;(2)10,5
例1、解:∵ 四边形ABCD是矩形,∴AC与BD相等且互相平分.∴OA=OB.
∵∠AOB=60°,∴△OAB是等边三角形.
∴矩形的对角线长AC=BD = 2OA=2×4=8(cm).
变式1、解:∵四边形ABCD是矩形,∴AC与BD相等且互相平分,∠ABC=90°.
∴OA=OB=AC=4.∵∠AOD=120°∴∠AOB=60°,∴△OAB是等边三角形.∴AB=OA=4
在Rt△ABC中,根据勾股定理得,BC=∴AB=4,BC=
变式2、解:设AD=x cm,则对角线长(x+4)cm,在Rt△ABD中,由勾股定理:,解得x=6. 则 AD=6cm.
根据等面积法得AE×DB= AD×AB,解得 AE= 4.8cm.
变式3、证明:∵ 四边形ABCD是矩形,∴ ∠B=90°,且AD∥BC. ∴ ∠1=∠2.
∵ DF⊥AE, ∴ ∠AFD=90°. ∴ ∠B=∠AFD.
又 AD=AE,∴ △ABE≌△DFA(AAS).
∴ AF=BE.∴ EF=EC.
此题还可以连接DE,证明△DEF≌△DEC,得到EF=EC.
四、C/C/B 4、(1)60°、120°、60°、120°(2)5、、5、
5、解:∵四边形ABCD是矩形 ∴AB∥CD,AD=BC,∠D=∠ABC=90° ∴∠AED=∠EAB
∵AB=2BC,且AB=AE ∴AE=2AD
∵∠D=90° ∴△ADE是直角三角形 ∴∠AED=30°∴∠EAB=30°
∵AB=AE ∴∠AEB=∠ABE=75° ∴∠CBE=∠ABC - ∠ABE= 15°
选做题:证明:∵四边形ABCD是矩形 ∴∠B=∠C=90°,AB=CD
∵E是BC的中点 ∴BE=CE=BC
∵BC=2AB ∴AB=BE=CE=DE ∴∠AEB=∠DEC=45°
∴∠AED=180°-∠AEB -∠DEC=180°-45°-45°=90° ∴EA⊥ED
课题 18.2.1矩形的性质 课型 新授
学习 目标 1.掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系.
2.会初步运用矩形的概念和性质来解决有关问题.
学习 关键 重点 矩形的性质
难点 矩形的性质的灵活应用
学教过程
创设情境独立思考 1、阅读课本P52 ~53 页,思考下列问题:
(1)什么是矩形?矩形是平行四边形吗?
矩形有哪些性质?
边:
角:
对角线:
对称性:
直角三角形斜边的中线和斜边有什么关系?为什么?
二、自学检测
1.矩形具有而平行四边行不具有的的性质是( )
A、对角相等 B、对角线相等 C、对角线互相平分 D、对边平行且相等
2.已知:四边形ABCD是矩形,
(1)若已知AB=8㎝,AD=6㎝,则AC=_____ ㎝,OB=_____ ㎝
(2)若已知∠DOC=120°,AC=8㎝,则AD=____cm,AB=____cm
3.已知△ABC是Rt△,∠ABC=90°,BD是斜边AC上的中线,
(1)若BD=3㎝,则AC= ㎝
(2)若∠C=30°,AB=5㎝,则AC= ㎝,BD= ㎝
三、例题精讲
例1 已知:如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长.
变式1:已知:如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AC=8,求AB,BC
变式2:已知:如图 ,矩形 ABCD,AB长8 cm ,对角线比AD边长4 cm.
求AD的长及点A到BD的距离AE的长.
分析:(1)因为矩形四个角都是直角,因此矩形中计算经常要用
到直角三角形的性质、勾股定理及方程思想.
“直角三角形斜边上的高”是一个基本图形,利用等面积法。
变式3:已知:矩形ABCD中,E是BC上一点,DF⊥AE于F,若AE=BC.求证:CE=EF.
分析:CE、EF分别是BC,AE等线段上的一部分,若AF=BE,则问题解决,而证明AF=BE,只要证明△ABE≌△DFA即可,在矩形中容易构造全等的直角三角形.
四、达标检测
1.(4分)矩形的两条对角线的夹角为60°,对角线长为15cm,较短边的长为( ).
(A)12cm (B)10cm (C)7.5cm (D)5cm
2.(4分)下列说法错误的是( ).
(A)矩形的对角线互相平分 (B)矩形的对角线相等
(C)有一个角是直角的四边形是矩形 (D)有一个角是直角的平行四边形叫做矩形
3.(4分)矩形的对角线把矩形分成的三角形中全等三角形一共有( ).
(A)2对 (B)4对 (C)6对 (D)8对
4.(4分)(1)已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为 、 、 、 .
(2)已知矩形的一条对角线长为10cm,两条对角线的一个交角为120°,则矩形的边长分别为 cm, cm, cm, cm.
5.(8分)如图,矩形ABCD中,AB=2BC,且AB=AE,求∠CBE的度数.
选做题:(8分)已知:矩形ABCD中,BC=2AB,E是BC的中点,求证:EA⊥ED.
答案:
二、1、B 2、(1)10,5;(2)4, 3、(1)6;(2)10,5
例1、解:∵ 四边形ABCD是矩形,∴AC与BD相等且互相平分.∴OA=OB.
∵∠AOB=60°,∴△OAB是等边三角形.
∴矩形的对角线长AC=BD = 2OA=2×4=8(cm).
变式1、解:∵四边形ABCD是矩形,∴AC与BD相等且互相平分,∠ABC=90°.
∴OA=OB=AC=4.∵∠AOD=120°∴∠AOB=60°,∴△OAB是等边三角形.∴AB=OA=4
在Rt△ABC中,根据勾股定理得,BC=∴AB=4,BC=
变式2、解:设AD=x cm,则对角线长(x+4)cm,在Rt△ABD中,由勾股定理:,解得x=6. 则 AD=6cm.
根据等面积法得AE×DB= AD×AB,解得 AE= 4.8cm.
变式3、证明:∵ 四边形ABCD是矩形,∴ ∠B=90°,且AD∥BC. ∴ ∠1=∠2.
∵ DF⊥AE, ∴ ∠AFD=90°. ∴ ∠B=∠AFD.
又 AD=AE,∴ △ABE≌△DFA(AAS).
∴ AF=BE.∴ EF=EC.
此题还可以连接DE,证明△DEF≌△DEC,得到EF=EC.
四、C/C/B 4、(1)60°、120°、60°、120°(2)5、、5、
5、解:∵四边形ABCD是矩形 ∴AB∥CD,AD=BC,∠D=∠ABC=90° ∴∠AED=∠EAB
∵AB=2BC,且AB=AE ∴AE=2AD
∵∠D=90° ∴△ADE是直角三角形 ∴∠AED=30°∴∠EAB=30°
∵AB=AE ∴∠AEB=∠ABE=75° ∴∠CBE=∠ABC - ∠ABE= 15°
选做题:证明:∵四边形ABCD是矩形 ∴∠B=∠C=90°,AB=CD
∵E是BC的中点 ∴BE=CE=BC
∵BC=2AB ∴AB=BE=CE=DE ∴∠AEB=∠DEC=45°
∴∠AED=180°-∠AEB -∠DEC=180°-45°-45°=90° ∴EA⊥ED
