9.2.3总体集中趋势估计-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(共16张PPT)
文档属性
| 名称 | 9.2.3总体集中趋势估计-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 763.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 21:41:59 | ||
图片预览





文档简介
(共16张PPT)
9.2.3
总体集中趋势的估计
⑵中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数.
⑴众数:在一组数据中,出现次数最多的数据叫做这组数据的众数.
众数、中位数、平均数都是描述一组数据的集中趋势的特征数,只是描述的角度不同,其中以平均数的应用最为广泛.
⑶平均数:一组数据的算术平均数,即
一、基础知识讲解
(一)基本概念
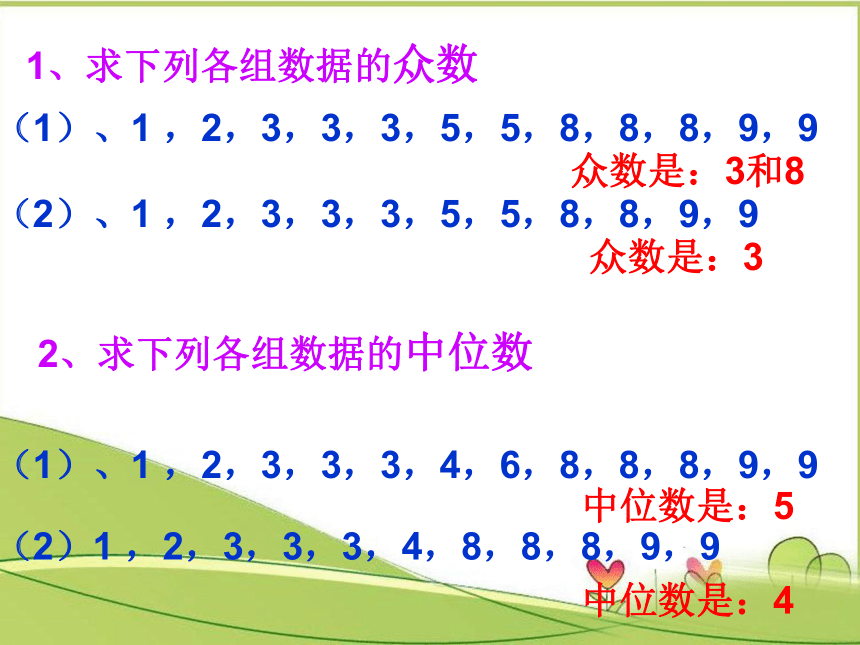
1、求下列各组数据的众数
(1)、1
,2,3,3,3,5,5,8,8,8,9,9
众数是:3和8
(2)、1
,2,3,3,3,5,5,8,8,9,9
众数是:3
2、求下列各组数据的中位数
(1)、1
,2,3,3,3,4,6,8,8,8,9,9
(2)1
,2,3,3,3,4,8,8,8,9,9
中位数是:5
中位数是:4
例4.
利用9.2.1节中100户居民用户的月均用水量
的调查数据,计算样本数据的平均数和中位数,并据
此估计全市居民用户月均用水量的平均数和中位数.
解:
2.平均数、中位数、众数刻画一组数据的集中趋势的特点
小明用统计软件计算了100户居民用水量的平均
平均数和中位数.但在录入数据时,不小心把一个数
据7.7录成了77.请计算录入数据的平均数和中位数,
并与真实的样本平均数和中位数作比较.哪个量的
变化更大?你能解释其中的原因吗?(p204
思考)
平均数(由8.79变为9.483)比中位数对样本中
的极端值更加敏感
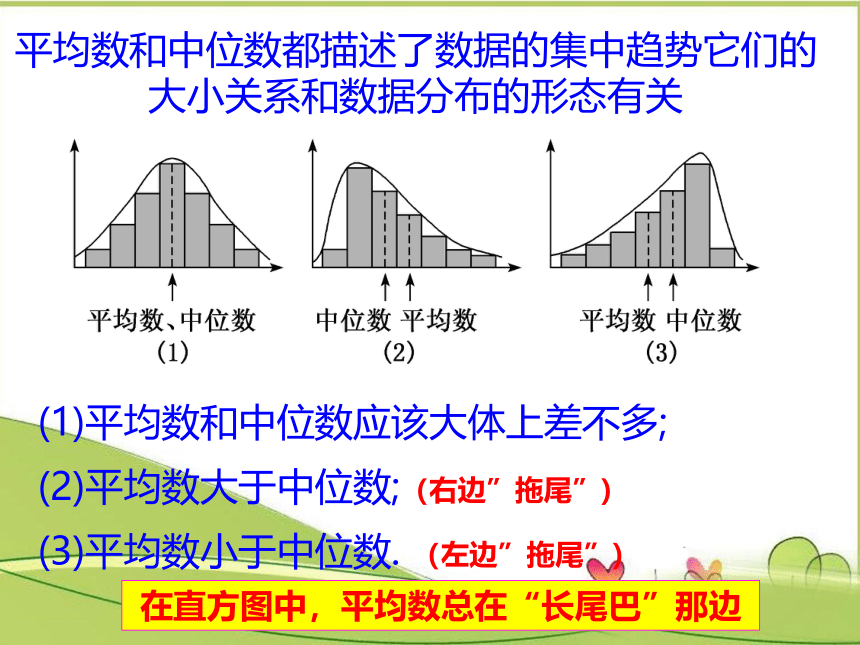
平均数和中位数都描述了数据的集中趋势它们的大小关系和数据分布的形态有关
(1)平均数和中位数应该大体上差不多;
(2)平均数大于中位数;(右边”拖尾”)
(3)平均数小于中位数.
(左边”拖尾”)
在直方图中,平均数总在“长尾巴”那边
由频率分布直方图估计平均数、众数、中位数
可以从频率分布直方图中估计平均数。平均数是频率分布直方图的“重心”等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和。
(1)平均数的估计
月均用水量/t
频率/组距
0.02
1.2
4.2
7.2
10.2
13.2
16.2
19.2
22.2
25.2
28.2
0
0.04
0.06
0.08
0.1
0.12
0.077
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
(2)中位数的估计
在频率分布直方图中,中位数左边和右边的直方图的面积各为0.5,
即在直方图中位数左右的面积相等.
月均用水量/t
频率/组距
0.02
1.2
4.2
7.2
10.2
13.2
16.2
19.2
22.2
25.2
28.2
0
0.04
0.06
0.08
0.1
0.12
0.077
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
(3)众数的估计
众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标.
月均用水量/t
频率/组距
0.02
1.2
4.2
7.2
10.2
13.2
16.2
19.2
22.2
25.2
28.2
0
0.04
0.06
0.08
0.1
0.12
0.077
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
1、已知200辆汽车通过某一段公路时的时速的频率分布直方图
如图所示,时速在[60,70)的汽车大约有________辆.
该图的众数
平均数为
中位数
80
65
62
62.5
众数:最高矩形的中点
中位数:左右两边面积相等
平均数等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和
练
从频率分布直方图中找众数、中位数、平均数
众数:
最高矩形的中点
优点:反映样本数据的最大集合点
缺点:忽视了其他数据,无法客观的反映总体特征
中位数:中位数左边的直方图面积和右边的直方图面积相等
优点:不受少数几个极端值的影响
缺点:不受少数几个极端值的影响
平均数:直方图的“重心”
优点:和每一个样本数据都有关,可以放映更多的关于样本数据的信息
缺点:离平均数越远的数据对平均数影响越大(可靠性低)
练1、某学习小组在一次数学测验中,得100分的有1人,95分的有1人,90分的有2人,85分的有4人,80分和75分的各有1人,则该小组成绩的平均数、众数、中位数分别是
( )
A.85,85,85
B.87,85,86
C.87,85,85
D.87,85,90
解析:从小到大列出所有数学成绩:75,80,85,85,85,85,90,90,
95,100,观察知众数和中位数均为85,计算得平均数为87.
C
练3:据了解,某公司的33名职工月工资(单位:元)如下:
职务
董事长
副董事长
董事
总经理
经理
管理员
职员
人数
1
1
2
1
5
3
20
工资
11
000
10
000
9
000
8
000
6
500
5
500
4
000
(1)求该公司职工月工资的平均数、中位数、众数;
(2)假设副董事长的工资从10
000元提升到20
000元,董事长的工资从11
000元提升到30
000元,那么新的平均数、中位数、众数又是多少(精确到元)?
(3)你认为哪个统计量更能反映这个公司员工的工资水平?结合此问题谈一谈你的看法.
五、课时小结
把一组数据按大小顺序排列,处在最中间的一个数据(或两个数据的平均数);
从频率分布直方图中估计中位数左右两边的直方图的面积相等.
一组数据中重复出现次数最多的数;
从频率分布直方图
中估计众数是最高的矩形的中点.
1.众数
2中位数
3平均数
如果有n个数据
那么这n个数的平均数
也可以从频率分布直方图中估计平均数,平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中的横坐标之和.
9.2.3
总体集中趋势的估计
⑵中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数.
⑴众数:在一组数据中,出现次数最多的数据叫做这组数据的众数.
众数、中位数、平均数都是描述一组数据的集中趋势的特征数,只是描述的角度不同,其中以平均数的应用最为广泛.
⑶平均数:一组数据的算术平均数,即
一、基础知识讲解
(一)基本概念
1、求下列各组数据的众数
(1)、1
,2,3,3,3,5,5,8,8,8,9,9
众数是:3和8
(2)、1
,2,3,3,3,5,5,8,8,9,9
众数是:3
2、求下列各组数据的中位数
(1)、1
,2,3,3,3,4,6,8,8,8,9,9
(2)1
,2,3,3,3,4,8,8,8,9,9
中位数是:5
中位数是:4
例4.
利用9.2.1节中100户居民用户的月均用水量
的调查数据,计算样本数据的平均数和中位数,并据
此估计全市居民用户月均用水量的平均数和中位数.
解:
2.平均数、中位数、众数刻画一组数据的集中趋势的特点
小明用统计软件计算了100户居民用水量的平均
平均数和中位数.但在录入数据时,不小心把一个数
据7.7录成了77.请计算录入数据的平均数和中位数,
并与真实的样本平均数和中位数作比较.哪个量的
变化更大?你能解释其中的原因吗?(p204
思考)
平均数(由8.79变为9.483)比中位数对样本中
的极端值更加敏感
平均数和中位数都描述了数据的集中趋势它们的大小关系和数据分布的形态有关
(1)平均数和中位数应该大体上差不多;
(2)平均数大于中位数;(右边”拖尾”)
(3)平均数小于中位数.
(左边”拖尾”)
在直方图中,平均数总在“长尾巴”那边
由频率分布直方图估计平均数、众数、中位数
可以从频率分布直方图中估计平均数。平均数是频率分布直方图的“重心”等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和。
(1)平均数的估计
月均用水量/t
频率/组距
0.02
1.2
4.2
7.2
10.2
13.2
16.2
19.2
22.2
25.2
28.2
0
0.04
0.06
0.08
0.1
0.12
0.077
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
(2)中位数的估计
在频率分布直方图中,中位数左边和右边的直方图的面积各为0.5,
即在直方图中位数左右的面积相等.
月均用水量/t
频率/组距
0.02
1.2
4.2
7.2
10.2
13.2
16.2
19.2
22.2
25.2
28.2
0
0.04
0.06
0.08
0.1
0.12
0.077
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
(3)众数的估计
众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标.
月均用水量/t
频率/组距
0.02
1.2
4.2
7.2
10.2
13.2
16.2
19.2
22.2
25.2
28.2
0
0.04
0.06
0.08
0.1
0.12
0.077
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
1、已知200辆汽车通过某一段公路时的时速的频率分布直方图
如图所示,时速在[60,70)的汽车大约有________辆.
该图的众数
平均数为
中位数
80
65
62
62.5
众数:最高矩形的中点
中位数:左右两边面积相等
平均数等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和
练
从频率分布直方图中找众数、中位数、平均数
众数:
最高矩形的中点
优点:反映样本数据的最大集合点
缺点:忽视了其他数据,无法客观的反映总体特征
中位数:中位数左边的直方图面积和右边的直方图面积相等
优点:不受少数几个极端值的影响
缺点:不受少数几个极端值的影响
平均数:直方图的“重心”
优点:和每一个样本数据都有关,可以放映更多的关于样本数据的信息
缺点:离平均数越远的数据对平均数影响越大(可靠性低)
练1、某学习小组在一次数学测验中,得100分的有1人,95分的有1人,90分的有2人,85分的有4人,80分和75分的各有1人,则该小组成绩的平均数、众数、中位数分别是
( )
A.85,85,85
B.87,85,86
C.87,85,85
D.87,85,90
解析:从小到大列出所有数学成绩:75,80,85,85,85,85,90,90,
95,100,观察知众数和中位数均为85,计算得平均数为87.
C
练3:据了解,某公司的33名职工月工资(单位:元)如下:
职务
董事长
副董事长
董事
总经理
经理
管理员
职员
人数
1
1
2
1
5
3
20
工资
11
000
10
000
9
000
8
000
6
500
5
500
4
000
(1)求该公司职工月工资的平均数、中位数、众数;
(2)假设副董事长的工资从10
000元提升到20
000元,董事长的工资从11
000元提升到30
000元,那么新的平均数、中位数、众数又是多少(精确到元)?
(3)你认为哪个统计量更能反映这个公司员工的工资水平?结合此问题谈一谈你的看法.
五、课时小结
把一组数据按大小顺序排列,处在最中间的一个数据(或两个数据的平均数);
从频率分布直方图中估计中位数左右两边的直方图的面积相等.
一组数据中重复出现次数最多的数;
从频率分布直方图
中估计众数是最高的矩形的中点.
1.众数
2中位数
3平均数
如果有n个数据
那么这n个数的平均数
也可以从频率分布直方图中估计平均数,平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中的横坐标之和.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
