9.1 锐角三角比

(共17张PPT)
9.1 锐角三角比


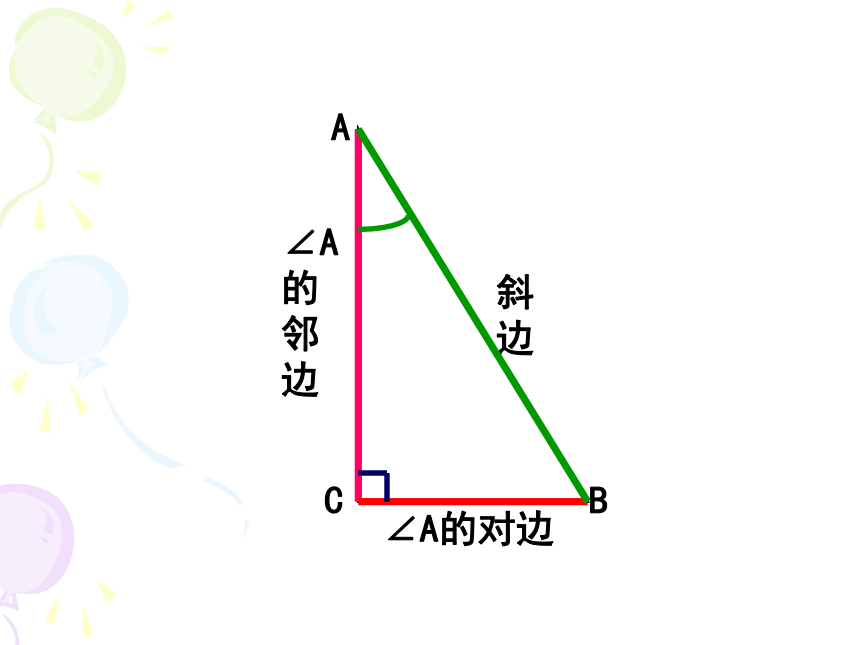
∠A的对边
∠A的邻边
C
A
B
斜边
C1
C3
C2
B1
B2
B3
A
M
N
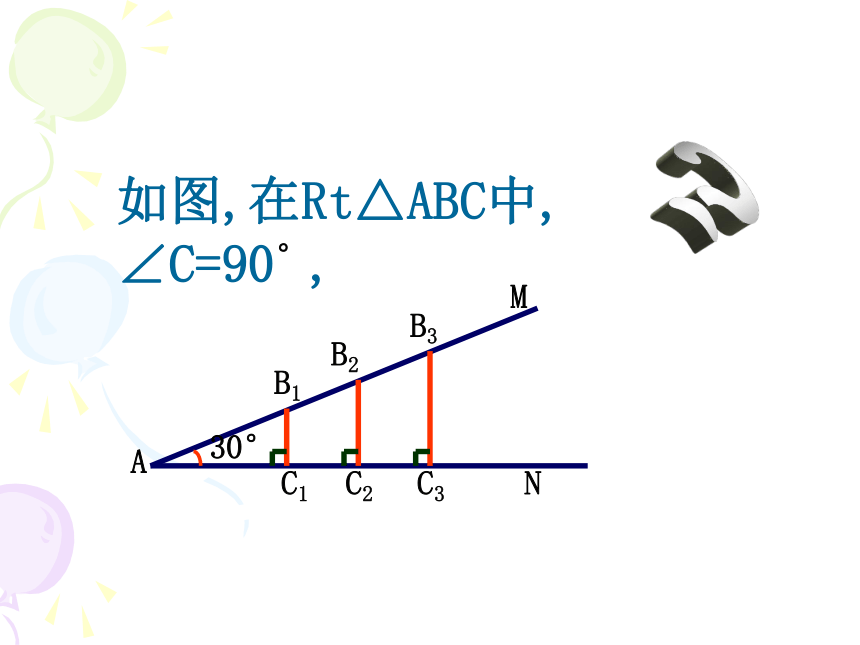
30°
如图,在Rt△ABC中, ∠C=90°,
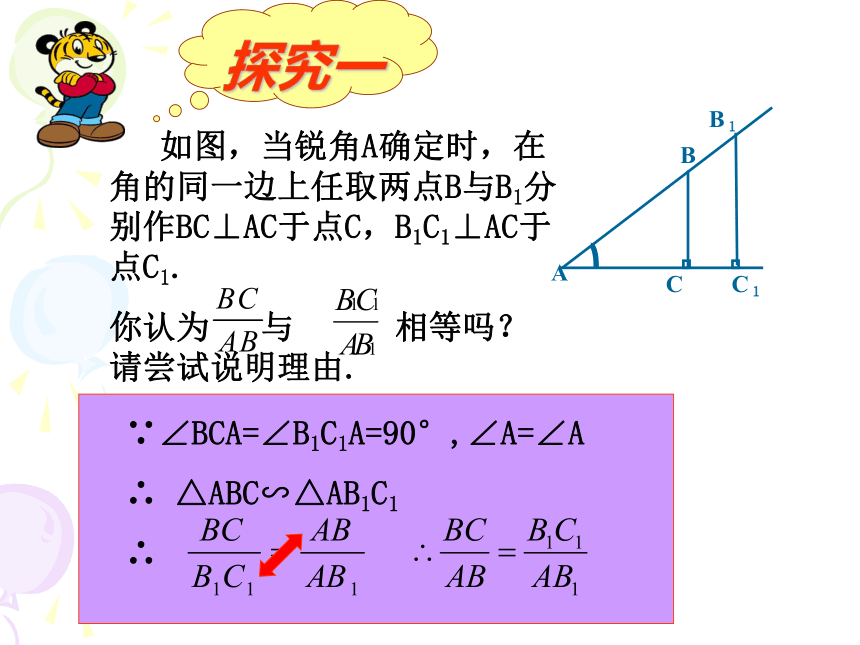
如图，当锐角A确定时，在角的同一边上任取两点B与B1分别作BC⊥AC于点C，B1C1⊥AC于点C1.
你认为　 与　　　相等吗？请尝试说明理由.
A
B１
B
C
C１
探究一
∵∠BCA=∠B1C1A=90°,∠A=∠A
∴ △ABC∽△AB1C1
∴
当锐角A的值发生变化时，它的对边与斜边的比值k的大小发生变化了吗？
猜想园地
直角三角形中锐角A的对边与斜边的比值k随着角度的变化而变化
当锐角A的大小确定后，不论以∠ A为内角的直角三角形的大小如何， ∠ A的对边与斜边的比值是一个定值，我们把这个确定的值叫做∠A的正弦，记作sinA 即
sin A=
1.sin∠A通常省略“∠”写成sinA的形式
2.sinA 不是一个角，是一个比值，没有单位
3.sinA不是 sin与A的乘积
如图,在Rt△ABC中, ∠C=900,当锐角A确定时, 大胆猜想一下这三边中还有哪两边的比值也可能是一个定值？
∠A的
∠A的
A
B１
B
C
C１
①证得△ABC∽△AB1C1
可得 得：
可得 得：
②证得△ABC∽△AB1C1
锐角A的邻边与斜边的比值叫做∠A的余弦
记作 cosA 即
cosA=
锐角A的对边与邻边的比值叫做∠A的余弦，记作 tanA 即
tanA=
如图，在Rt△ABC中，∠C＝90°，AC=4,BC=2,求∠A的正弦、余弦、正切的值．
A
B
C
2
解：在Rt△ABC中，∠C=90°
4
练习巩固
1、如图,在Rt△ABC中,∠C=90°， AB=3,BC=2,求∠B的正弦，余弦，正切值。
解：在Rt△ABC中，C=90°
C
A
B
3
2
2、如图,在Rt△ABC中,∠C=90°，AB=2AC, 求sinA和tanA的值
A
C
B
解：设AC=X,则AB=2X
根据勾股定理可得BC= X
∴sinA= =
tanA=
学习了一个重要概念：锐角三角函数
经历了一个探究过程：特殊到一般
体现了一种数学思想：数形结合
体验到一种学习方法：猜想　　证明　　归纳　　应用
小结梳理：我们学习了－－－－
∠α的正弦sin α =
∠α的余弦cos α =
∠α的正切 tan α =
在直角三角形中， 若∠α是其中一个锐角，则有：
1.判断对错:
A
B
C
如图 (1)sinA= （ ）
(2)sinB= （ ）
(3)tanA= （ ）
√
×
×
2、如图，在Rt△ABC中，∠C＝90°，求∠A的正弦、余弦、正切的值．
A
B
C
13
5
解：在Rt△ABC中，C=90°
课后延伸
1.必做题：P63A组1.3题；
2.选做题：见导学案
3.预习P65-66内容