水溶液中的离子平衡
图片预览

















































































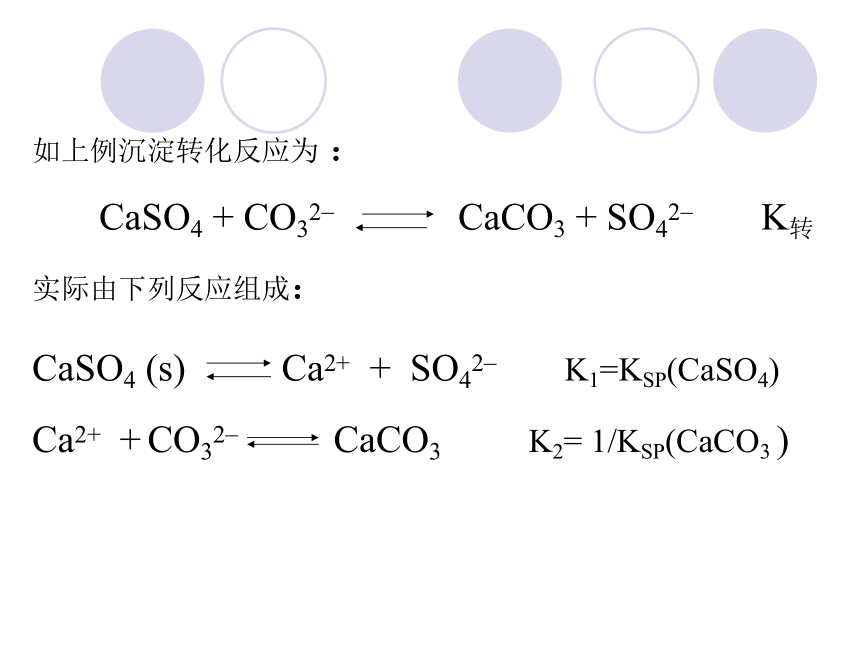

文档简介
(共98张PPT)
祝大家新年快乐!
第九章 水溶液中的离子平衡
第九章 水溶液中的离子平衡
一、酸碱平衡
二、配离子平衡
三、难溶电解质的离子平衡
电解质和非电解质
强电解质和弱电解质
温故而知新
Fe
CO2
SO2
Al2O3
CaCO3
SO3
H2SO4
H2O
NH3·H2O
H2SO3
NaCl
NaHSO4
C2H5OH
NH3
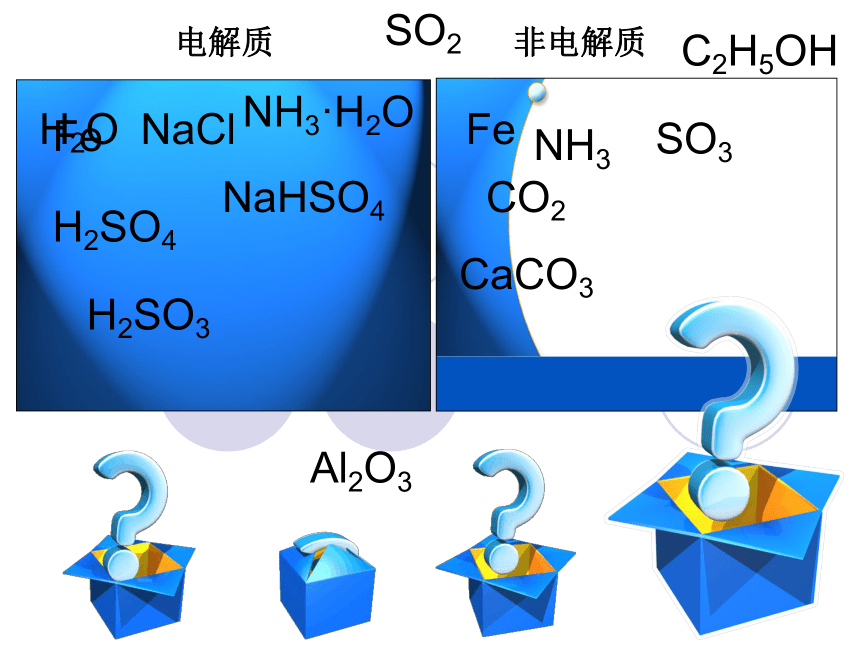
电解质
非电解质
Fe
Fe
NaCl
NaHSO4
H2SO4
SO2
CO2
Al2O3
NH3·H2O
CaCO3
C2H5OH
H2SO3
SO3
NH3
H2O
能导电的物质一定是电解质?
不导电的物质一定是非电解质?
第九章 水溶液中的离子平衡
一、酸碱平衡
1.掌握解离度、解离常数、共轭酸碱对、缓冲溶液、同离子效应等基本概念
2.掌握酸碱质子理论、酸碱反应的实质、质子自递反应、共轭酸碱对的解离常数的关系
3.掌握强酸碱溶液、弱酸碱溶液、缓冲溶液的H+浓度的计算。
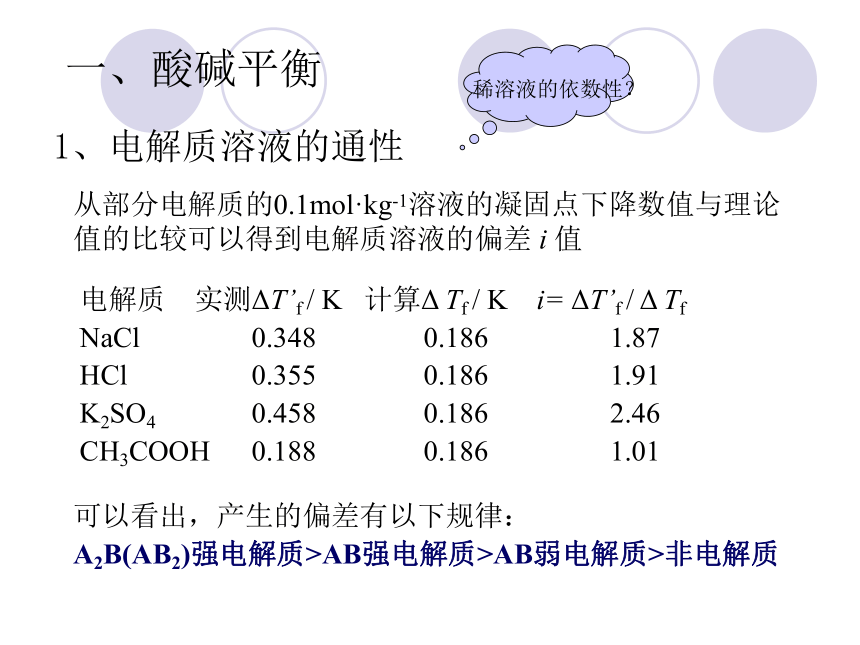
1、电解质溶液的通性
从部分电解质的0.1mol·kg-1溶液的凝固点下降数值与理论值的比较可以得到电解质溶液的偏差 i 值
电解质 实测ΔT’f / K 计算Δ Tf / K i= ΔT’f / Δ Tf
NaCl 0.348 0.186 1.87
HCl 0.355 0.186 1.91
K2SO4 0.458 0.186 2.46
CH3COOH 0.188 0.186 1.01
可以看出,产生的偏差有以下规律:
A2B(AB2)强电解质>AB强电解质>AB弱电解质>非电解质
一、酸碱平衡
稀溶液的依数性?
1、电解质溶液的通性
阿仑尼乌斯根据电解质溶液不服从稀溶液依数性的现象,提出了电离理论。
电离理论认为电解质分子在水溶液中解离
成离子,使得溶液中的微粒数增大,故它们的蒸汽压、沸点、熔点的改变和渗透压数值都比非电解质大。
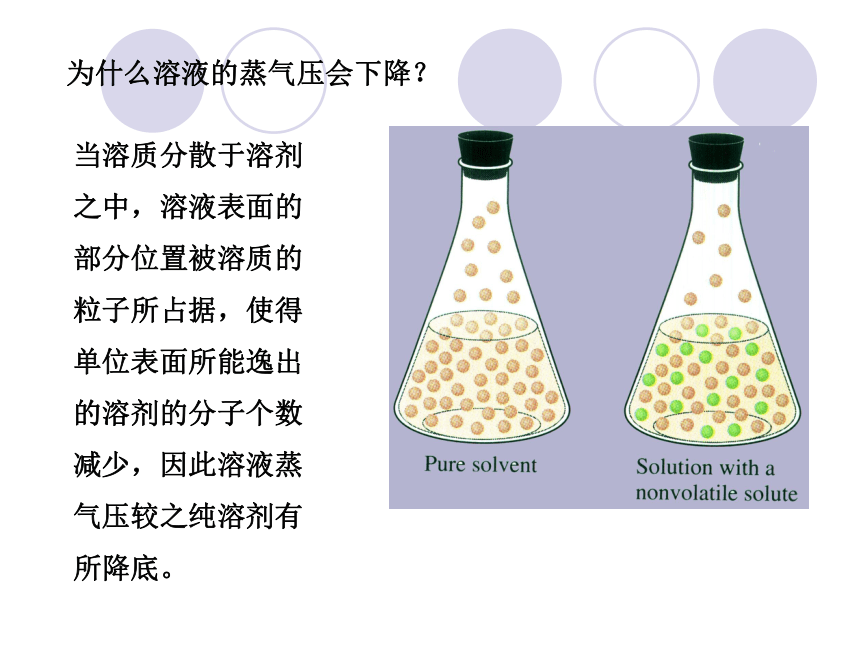
为什么溶液的蒸气压会下降?
当溶质分散于溶剂之中,溶液表面的部分位置被溶质的粒子所占据,使得单位表面所能逸出的溶剂的分子个数减少,因此溶液蒸气压较之纯溶剂有所降底。
1、电解质溶液的通性
解离度——
溶液中已解离的电解质的分子数与电解质总分子数之比。
2、水溶液中的单相离子平衡
水溶液中的单相离子平衡一般分为酸、碱的解离平衡及配离子的解离平衡两类。
根据解离度的大小,将电解质分为:
强电解质和弱电解质两类。
强电解质在水中全部解离,而弱电解质在水溶液中只有部分解离,大部分仍以分子形式存在。弱电解质在水溶液中存在解离平衡。
强电解质
弱电解质
H2SO4
CaCO3
Ca(OH)2
Fe(OH)3
H2CO3
NaHCO3
NH3·H2O
C12H22O11
按先后次序,酸碱理论主要有以下几种:
a.酸碱电离理论(阿氏水离子论)
在水溶液中解离时所生成的正离子全部是H+的化合物是酸;所生成的负离子全部是OHˉ的化合物是碱。
酸碱中和反应的实质是H+ + OHˉ = H2O。
酸碱电离理论的缺陷:
把酸、碱的定义局限于以水为溶剂的系统。
无法解释NH3、Na2CO3均不含OHˉ,也具有碱性。
3、酸碱的概念
b.酸碱质子理论
凡能给出质子的物质都是酸;
凡能结合质子的物质都是碱。
在水溶液中
HCl(aq)= H+(aq) +Cl-(aq)
HAc(aq) H+(aq) +Acˉ(aq)
NH4+(aq) H+(aq) +NH3(aq)
HCO3-(aq) H+(aq) + CO32-(aq)
酸 质子 + 碱
b.酸碱质子理论
在水溶液中
HCl(aq)= H+(aq) +Cl-(aq)
HAc(aq) H+(aq) +Acˉ(aq)
NH4+(aq) H+(aq) +NH3(aq)
HCO3-(aq) H+(aq) + CO32-(aq)
酸、碱可以是分子,也可以是离子。
酸给出质子后可以再结合质子,因此酸给出质子后就变为碱:
酸 质子 + 碱
(质子给予体) (质子接受体)
b.酸碱质子理论
共轭酸碱概念
酸与对应的碱的这种相互依存、相互转化的关系称为酸碱共轭关系。
酸失去质子后形成的碱被称为该酸的共轭碱;碱结合质子后形成的酸被称为该碱的共轭酸。
共轭酸与它的共轭碱一起称为共轭酸碱对。例如:
(1)
a.因一个质子的得失而互相转变的每一对酸和碱,称为共轭酸碱对(如:HAc-Ac-),彼此相差一个H+。
b.酸碱的定义是广义的,酸碱可以是分子,也可以是阳离子、阴离子。
c.酸碱具有相对性。既可失去质子、又可得到质子的物质,称为两性物质。如:HCO3-、HPO4-等。
酸
碱半
反
应
b.酸碱质子理论
酸碱反应 是两对共轭酸碱对共同作用的结果。
共轭酸碱对
HAc + H2O H3O+ +Ac- (电离)
H3O+ +NH3 H2O+ NH4 (中和)
H2O+ CN- OH- + HCN (水解)
H2O+ CO3 HCO3 + OHˉ(水解)
2-
–
+
b.酸碱质子理论
酸碱反应 是两对共轭酸碱对共同作用的结果。
共轭酸碱对
HAc + H2O H3O+ +Ac- (电离) HAc/Ac-, H3O+/ H2O
H3O+ +NH3 H2O+ NH4 (中和) NH4 /NH3, H3O+/ H2O
H2O+ CN- OH- + HCN (水解) HCN/CN-, H2O/OH-
H2O+ CO3 HCO3 + OHˉ(水解) HCO 3/CO3, H2O/OH-
2-
–
+
+
–
2-
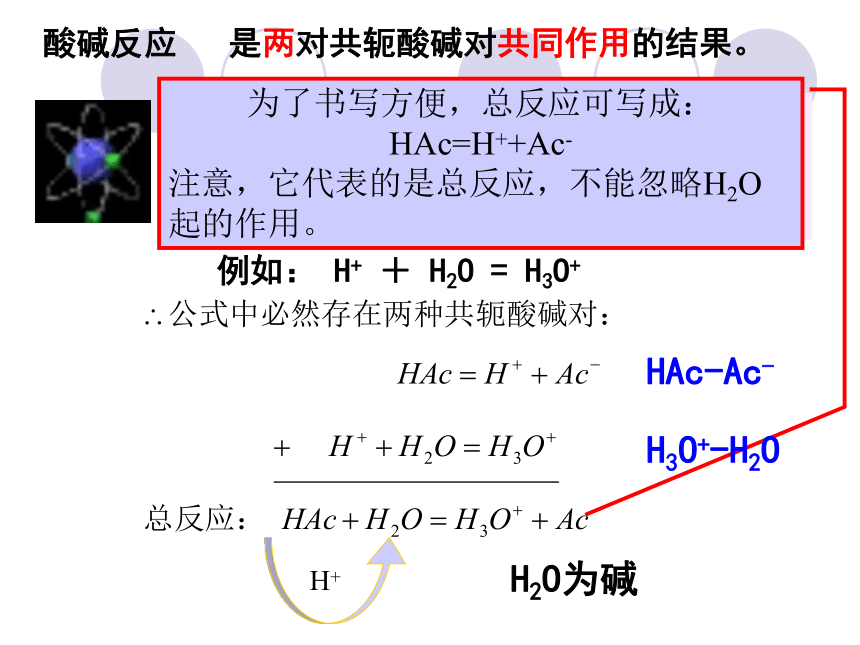
酸碱反应 是两对共轭酸碱对共同作用的结果。
H+就是一个原子核,光秃秃,半径小,又带正电荷,所以不能以游离状态存在, H+在水中的平均寿命只有10-14s。所以, H+一出现便立即附着于溶剂分子上,产生一种酸。
例如: H+ + H2O = H3O+
H+
为了书写方便,总反应可写成:
HAc=H++Ac-
注意,它代表的是总反应,不能忽略H2O起的作用。
HAc-Ac-
H3O+-H2O
H2O为碱
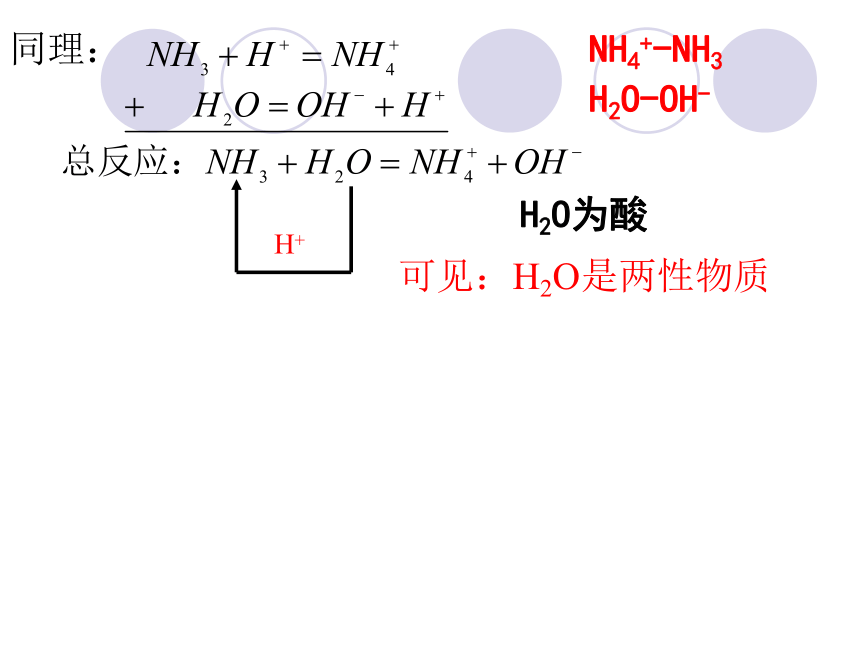
同理:
H+
可见:H2O是两性物质
H2O-OH-
NH4+-NH3
H2O为酸
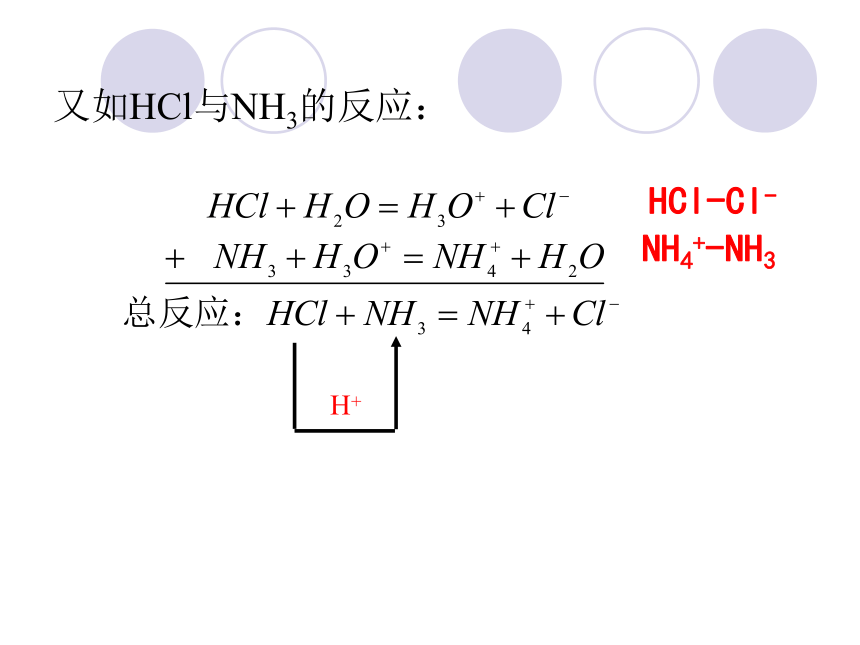
又如HCl与NH3的反应:
H+
NH4+-NH3
HCl-Cl-
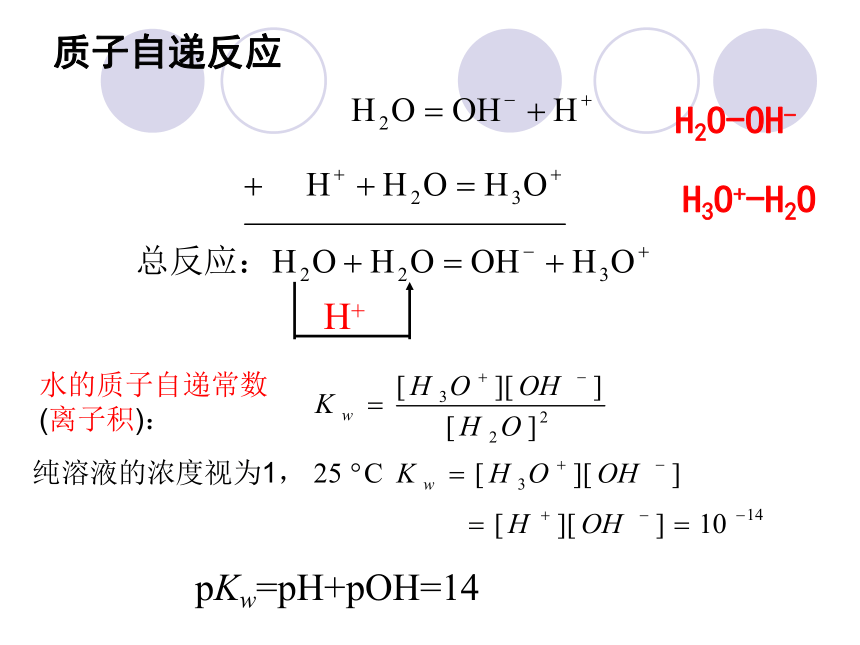
质子自递反应
H+
H2O-OH-
H3O+-H2O
水的质子自递常数(离子积):
纯溶液的浓度视为1,
pKw=pH+pOH=14
b.酸碱质子理论
酸碱质子理论扩大了酸碱的范围,它比电离理论更广泛,其酸碱的定义只以H+为判据,与溶剂无关,可以解释NH3、Na2CO3以及NH4Cl等的酸碱性。
两性物质: H2O, HCO3ˉ (所有酸式根)
无盐的概念: NH4Cl (酸碱复合物)
酸碱质子理论是概念的一场革新:
C.酸碱电子理论
凡能接受电子对的物质是酸,凡能给出电子对的物质是碱,也称为路易斯酸碱理论。
A+ B= A B
H+ + OH- = H2O
酸 + 碱 = 酸碱加合物
(1) H3BO3 + H2O [B(OH)4]ˉ + H+ (硼酸是路易斯酸)
Cu2+ + 4NH3 [Cu(NH3)4]2+ 深蓝色
酸 碱 加合物
酸碱电子理论摆脱了酸必须含有H的限制,包括的范围更广。
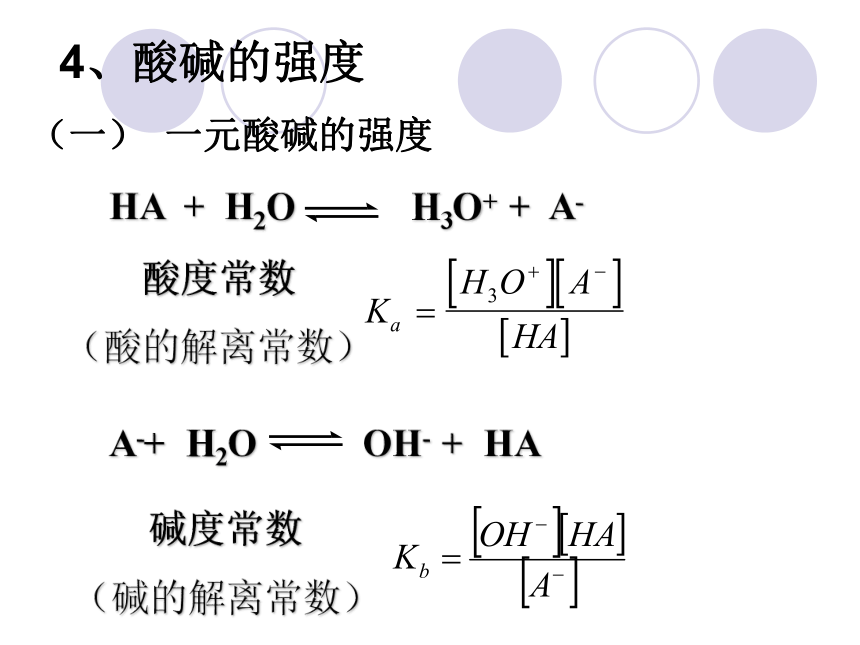
4、酸碱的强度
(一) 一元酸碱的强度
HA + H2O H3O+ + A-
酸度常数
(酸的解离常数)
A-+ H2O OH- + HA
碱度常数
(碱的解离常数)
讨论:
Ka↑,给质子能力↑强,酸的强度↑
Kb↑,得质子能力↑强,碱的强度↑
共轭酸碱对HA和A- 有如下关系
酸愈强,其共轭碱必定愈弱。
续
(二)多元酸碱的强度
H3PO4 H2PO4 - + H+
Ka1 Kb3
H2PO4- HPO42- + H+
Ka2 Kb2
HPO42- PO43- + H+
Ka3 Kb1
讨论:
多元酸碱在水中逐级离解,强度逐级递减
形成的多元共轭酸碱对中最强酸的解离常数
Ka1对应最弱共轭碱的解离常数Kb3
强酸强碱溶液pH值的计算
强酸(Ca )
HA H + + A -
H2O H + + OH -
当Ca > 10-6 mol/L,忽略水的解离
精确式
近似式***
5、酸碱溶液pH计算
当Ca < 10-8 mol/L, pH≈7
=
由水电离出的氢离子浓度和氢氧根离子浓度始终相等,不仅限于纯水中,对任何水溶液都成立。
续强酸强碱pH值计算
强碱(Cb )
精确式
B + H + BH +
H2O H + + OH –
近似式***
=
当Cb> 10-6 mol/L,忽略水的解离
一元弱酸和一元弱碱pH值的计算
设一元弱酸HA的浓度为c, 解离度为α
HA H+ + A-
起始浓度 c 0 0
平衡浓度 c(1-α) cα cα
因此
同理,对于一元弱碱:
溶液的酸度(H+离子浓度)常用pH表示, pH = –lg{c(H+)/c }, 溶液的碱度(OHˉ离子浓度)可用pOH表示。
当Kac≥20Kw, c/Ka≥500时,
例题
附例3.1 已知HAc的Ka =1.76×10-5,计算3.0%米醋(含HAc浓度为0.50 mol·dm-3)的pH。
解:设米醋溶液中H+的平衡浓度为x mol·dm-3, 则
HAc(aq) = H+(aq) + Ac-(aq)
平衡浓度/mol·dm-3 0.50 – x x x
Ka = 1.76×10-5
∵ c / Ka > 500 ∴ x很小,0.50 – x ≈ 0.5
pH = –lg c( H+)/c = –lg(2.97×10-3) = 3 – 0.47 = 2.53
例题
例3.2 计算0.100 mol·dm-3 NH4Cl溶液中H+浓度及其pH。
解: NH4Cl(aq) = NH4+(aq) + Clˉ(aq)
NH4+(aq) + H2O(l) = NH3(aq) + H3O+ (aq)
Ka =5.65×10-10
pH = – lg c( H+)/c = –lg(7.52×10-6) = 5.12
多元弱酸和多元弱碱pH值的计算
多元弱酸(碱)的解离是分级进行的,每一级解离都有一个解离常数,以磷酸为例:
一级解离:
二级解离:
三级解离:
说明
式中,Ka,3 << K a,2 << K a,1,每级解离常数差3~6个数量级。
因此, H+浓度的计算以一级解离为主。
计算H+浓度时,当Ka,2 / K a,1<10ˉ3时,可忽略二、三级解离平衡。
比较多元弱酸的酸性强弱时,只需比较它们一级解离常数值即可。
思考:根据反应式 H2S(aq) = 2H+(aq) + S2ˉ ,H+浓度是S2ˉ 离子浓度的两倍,此结论是否正确?
是错误的, H2S(aq)以一级电离为主,因此H2S溶液中c(H+) ≈ c(HSˉ)。
-
例题
附例3.3 已知 H2CO3的 Ka,1= 4.30×10-7, K a,2 = 5.61×10-11, 计算0.0200 mol·dm-3 H2CO3溶液中H+和 的浓度及pH。
解:∵Ka,2<pH = –lg 9. 27×10 –5 = 4 .03
H2CO3 H+ + HCO3 HCO3 H+ + CO32
第一步解离生成的H+抑制了第二步解离,因此 c(H+) ≈ c (HCO3 ) ≈ 9.27×10-5 mol·dm-3
c (CO32 ) = Ka,2 = 5.61×10-11 mol·dm-3
两性物质溶液pH值的计算
NaHA
Na H2PO4
Na2HPO4
缓冲溶液和pH的控制
同离子效应
在弱酸的溶液中加入该酸的共轭碱,或在弱碱的溶液中加入该碱的共轭酸
如HAc的水溶液中,
HAc(aq) = H+(aq) + Ac-(aq)
由于NaAc = Na++Acˉ
使得HAc解离平衡向左移动,HAc的解离度降低。
在弱酸的溶液中加入该酸的共轭碱,或在弱碱的溶液中加入该碱的共轭酸,使得弱酸或弱碱的解离度大大下降的现象,称为同离子效应。
加入NaAc,
例题
例3.3 在0.100 mol·dm-3HAc溶液中加入一定量固体NaAc,使NaAc的浓度等于0.100 mol·dm-3,求该溶液中H+浓度,pH和HAc的解离度α。
解:设已解离的HAc的浓度为x mol·dm-3
HAc = H+ + Ac
平衡浓度/mol·dm-3 0.1–x x 0.1+x
c(H+) = x mol·dm-3= 1.76 ×10-5 mol·dm-3, pH = 4.75
与例3.1相比,同离子效应使αHAc从1.34%降为0.018%, c(H+)从1.34 ×10-3 mol·dm-3 减少到1.76 ×10-5 mol·dm-3。
缓冲溶液
弱酸及其共轭碱或弱碱及其共轭酸所组成的溶液具有一个重要性质,该溶液的pH在一定范围内不因稀释或外加少量酸或碱而发生显著变化,即对外加的酸和碱具有缓冲能力,这种溶液称作缓冲溶液。
以HAc和NaAc的混合溶液为例:
NaAc == Na++ Ac-
HAc(aq) = H+(aq) + Ac-(aq)
系统中大量HAc、Acˉ存在,使H+相对较少。当溶液中加入少量强酸时,H+与Acˉ结合生成HAc,使H+的浓度保持基本不变。
若往系统中加入少量强碱,则H+与OH-结合生成H2O,使HAc解离平衡右移, HAc的浓度减少,而H+的浓度仍保持基本不变。
缓冲溶液的pH
当加入大量的强酸或强碱,使溶液中的Ac 或HAc耗尽,则溶液将失去缓冲能力。
组成缓冲溶液的一对共轭酸碱,如HAc–Ac 又称为缓冲对。可用通式表示缓冲对之间存在的平衡:
共轭酸 = 共轭碱 + H+
例题
附例3.4 40.00 cm3 1.00mol·dm-3 HAc与20.00cm3 1.00mol·dm-3 NaOH混合,求混合液的pH
解:HAc + NaOH = NaAc + H2O
由于HAc过量,反应平衡后生成0.02mol的Acˉ,并剩余0.02mol HAc,溶液总体积为60.00cm3。于是
已知HAc的pKa为4.76
因此
例题
解:50.00cm3缓冲溶液中加入盐酸后总体积为50.05 cm3,加入的1.000 mol·dm 3盐酸由于稀释,浓度变为:
由于加入的H+的量相对于溶液中Acˉ的量而言很小,可认为加入的H+完全与Acˉ结合成HAc分子。于是
c(HAc) = (0.1000 + 0.001)mol ·dm 3 = 0.101 mol ·dm 3,
c(Acˉ) = (0.1000 – 0.001)mol ·dm 3 = 0.099 mol ·dm 3
附例3.5 已知若在 50.00 cm3 含有 0.1000 mol·dm 3的HAc 和0.1000 mol·dm 3 NaAc缓冲液中,加入0.050 cm3 1.000 mol·dm 3 盐酸,求其pH。
说明
计算结果表明,50 cm3 HAc-NaAc缓冲溶液中,若加入少量的强酸(0.05cm3 1.0mol·dm-3的盐酸),溶液的pH由4.76降至4.74,仅改变0.02;但若在50cm3纯水中加入0.05cm3 1.0 mol·dm-3 HCl 溶液,则由于H+的浓度约为0.001mol·dm-3,pH等于3。即pH改变了4个单位。
思考:缓冲溶液的缓冲能力与哪些因素有关?
缓冲能力主要与以下因素有关:
缓冲溶液中共轭酸的pKa值:缓冲溶液的pH在其pKa值附近时,缓冲能力最大。
缓冲对的浓度:缓冲对的浓度均较大时,缓冲能力较大。
缓冲对的浓度比: 为1:1或相近(0.1~10)时,缓冲能力较大。
缓冲溶液的选择和配制
据所需pH选择缓冲对
缓冲溶液的pH不仅取决于缓冲对中共轭酸的Ka,还取决于缓冲对中两种物质浓度的比值。缓冲对中任一物质的浓度过小都会使溶液丧失缓冲能力,故两者浓度之比最好趋近于1,此时缓冲能力最强。
当c(共轭酸) = c(共轭碱)时,pH = pKa
因此选择缓冲体系时,应选择共轭酸的pKa与要求的pH相近的缓冲对。
一般认为,当缓冲对的浓度比在0.1和10之间才具有缓冲作用,因此,缓冲溶液的pH 和pKa之间有以下关系:
pH = pKa ± 1
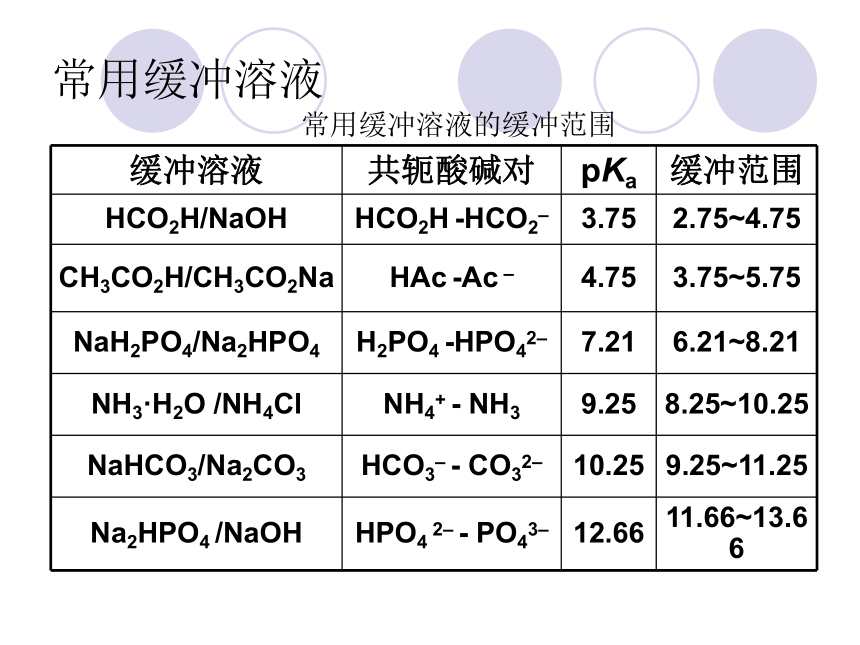
常用缓冲溶液
缓冲溶液 共轭酸碱对 pKa 缓冲范围
HCO2H/NaOH HCO2H -HCO2– 3.75 2.75~4.75
CH3CO2H/CH3CO2Na HAc -Ac – 4.75 3.75~5.75
NaH2PO4/Na2HPO4 H2PO4 -HPO42– 7.21 6.21~8.21
NH3·H2O /NH4Cl NH4+ - NH3 9.25 8.25~10.25
NaHCO3/Na2CO3 HCO3– - CO32– 10.25 9.25~11.25
Na2HPO4 /NaOH HPO4 2– - PO43– 12.66 11.66~13.66
常用缓冲溶液的缓冲范围
例题
附例3.6: 要配制10cm3 pH=5的HAc-NaAc缓冲液,问需浓度为1.0 mol·dm-3的HAc和NaAc溶液各多少毫升?
由于两者浓度相同,因此只需体积比和总体积满足:
V(HAc)/V(NaAc)=0.562 又V(HAc) + V(NaAc) = 10cm3
因此:V(HAc) = 3.6 cm3;V(NaAc) = 6.4 cm3
解:
练习
1. 已知0.1000mol/L HA溶液的pH=3,计算同浓度NaA溶液的pH值
解:
练习
3.某缓冲溶液100mL,HA的浓度为0.25mol/L(pKa=5.3),于此溶液中加入0.2g的NaOH(忽略体积变化)后,pH=5.6,问该缓冲溶 液原来的pH值是多少?
解:
练习
1、H2O的共轭酸是 ( )
A. H2O B. HAc C. H3O+ D. OH-
C
2、根据酸碱质子理论,正确的说法是 ( )
A. 酸愈强,则其共轭碱愈弱
B. H3O+是水溶液中的最强酸
C. H3O+的共轭碱是OH-
D. OH-是水溶液中的最强碱
A、B、D
3、根据酸碱质子理论下列化合物中不属于酸的是 ( )
A. HCO3- B. NH4+ C. HAc D. Ac-
D
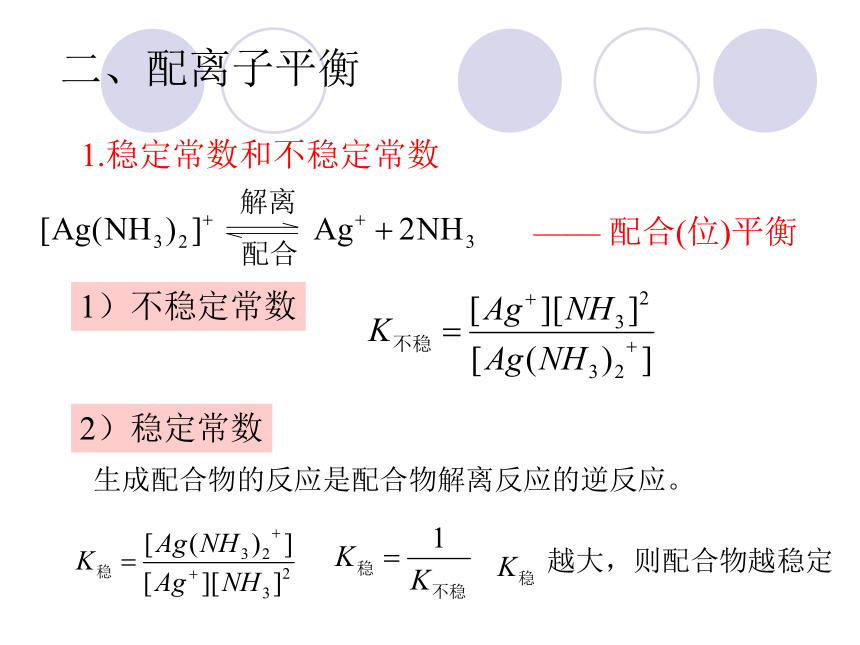
1.稳定常数和不稳定常数
解离
配合
—— 配合(位)平衡
1)不稳定常数
二、配离子平衡
2)稳定常数
生成配合物的反应是配合物解离反应的逆反应。
越大,则配合物越稳定
3)逐级稳定常数
4)累积稳定常数 ( β )
β 为各级配离子的稳定常数
2.稳定常数的应用
已知配位单元的浓度,利用标准稳定常数或标准不稳定常数可以计算配体和中心原子的平衡浓度。
(1)计算配位平衡的组成
例 计算0.10 mol·L-1[Ag(NH3) 2]+溶液中的Ag+
和 NH3 的浓度。
解:设溶液中Ag+的平衡浓度为 x mol·L-1,则有:
c0 /mol·L-1 0.10 0 0
c/mol·L-1 -x +x +2x
ceq/mol·L-1 0.10-x x 2x
标准平衡常数表达式为:
代入数据得:
由于 很小,因此 x 很小,可近似认为0.10-x=0.10 。由上式得:
解得:
溶液中 Ag+ 和 NH3 的平衡浓度分别为:
例 在 10.0 mL 0.040 mol·L-1 AgNO3 溶液中加
入10.0mL 2.0 mol·L-1 NH3 溶液,计算平衡溶液中配
体、中心原子和配位离子的浓度。
解:两种溶液混合后,Ag+ 和 NH3 的起始浓度为:
由于 NH3 过量,且 很大,可假定
Ag+全部生成 。再设平衡时
解离出的 Ag+ 浓度为 x mol·L-1,则:
ceq/mol·L-1
标准平衡常数表达式为:
代入数据得:
x =1.4×10-9
2.稳定常数的应用
(2) 判断配位反应进行的方向
在一种配位化合物的溶液中,加入另一种配体或中心原子,它也能与配位单元中的中心原子或配体发生配位反应,形成新的配位单元。利用标准平衡常数就可以判断反应进行的方向。如果配位反应的标准平衡常数很大,且加入的配体或中心原子的浓度足够大,则配位反应正向进行。
解:可能发生的反应:
[例题] 向含有 的溶液中加入KCN,
能否转化为
上述配位反应的标准平衡常数为:
K很大,配位反应向生成 [Ag(CN) 2]- 的正反应方向进行。若加入足量的 CN-,[Ag(NH3) 2]+ 可全部转化成 [Ag(CN) 2]-。
2.稳定常数的应用
(3)判断配离子与沉淀之间转化的可能性
一些难溶强电解质往往因形成配离子而溶解。利用配离子的标准稳定常数或标准不稳定常数,可以计算难溶电解质在有配体存在时的溶解度及全部转化为配离子时所需配体的浓度。
(4)配合物的生成对电极电势的影响
三、难溶电解质的离子平衡
难溶性物质一般是指在 100 克水中溶解的量少于 0.01 克的物质。但是有些物质并不符合这个标准,例如: PbCl2 CaSO4 HgSO4 g/100g H2O 0.675 0.176 0.055 由于这些物质的式量很大,所以其饱和溶液的物质的量浓度相当小,故这些化合物仍作为难溶性化合物讨论
讨论的对象是难溶性强电解质。
1、溶度积常数
沉淀-溶解平衡是当溶解和结晶速度相等时建立的平衡,是一种动态平衡。
此时的溶液是饱和溶液,它是多相平衡。其平衡关系为:
AgCl(s) Ag+ + Cl-
Ksp(AgCl) = [Ag+][Cl_]
KSP称为溶度积常数,简称溶度积。它反应了物质的溶解能力。
溶解
沉淀
难溶电解质溶度积常数通式:
AmBn mAn+ + nBm-
Ksp = [An+]m[Bm-]n
m、n分别代表电离方程式中A、B离子的化学计量数。
溶度积常数的意义:一定温度下,难溶强电解质饱和溶液中离子浓度的系数次方之积为一常数。
Ksp越大则难溶电解质在溶液中溶解趋势越大,反之越小。
例如:PbCl2(s) Pb2+(aq) + 2Cl-(aq) ;
Ksp=[Pb2+][Cl-]2
Fe(OH)3 Fe3+ + 3OH- ;
Ksp=[Fe3+][OH]3
2、溶度积与溶解度的关系
溶度积与溶解度都可表示物质的溶解能力,但它们既有区别又有联系。
一定温度下饱和溶液的浓度,也就是该溶质在此温度下的溶解度。溶质的溶解度为S,单位为mol.l-1,那么:
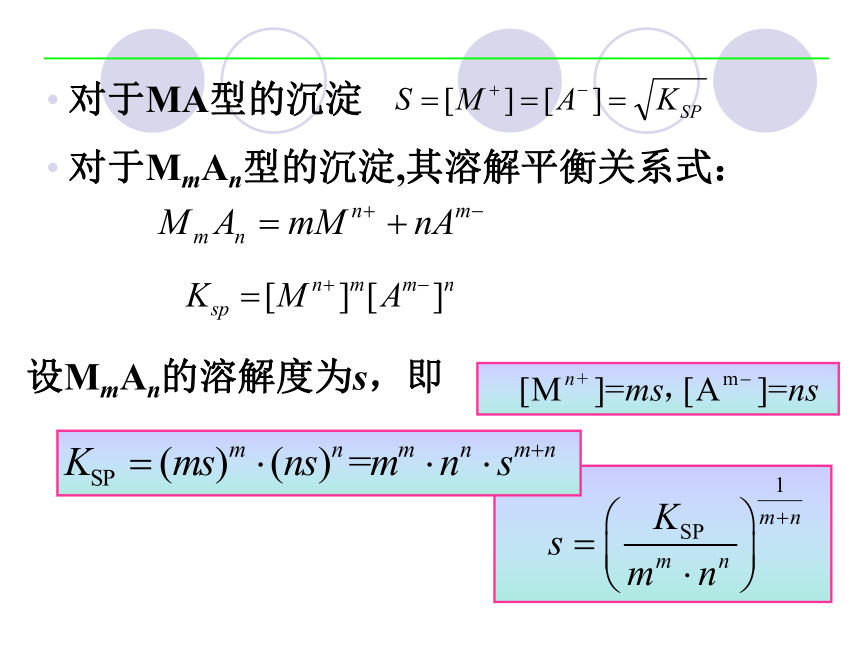
对于MA型的沉淀
对于MmAn型的沉淀,其溶解平衡关系式:
设MmAn的溶解度为s,即
如:已知AgCl、Ag2CrO4的溶度积,求AgCl、Ag2CrO4的溶解度。
AgCl(s) Ag+ + Cl-
S S
Ksp = [Ag+][Cl-] = S2 = 1.8*10-10
SAgCl = Ksp = 1.8*10-10
= 1.3*10-5mol.l-1
上式为AB型(1:1)溶解度计算式,同理可导出AB2和A2B型:
SAg2CrO4= =
=6.5*10-5mol.l-1
相同类型的电解质,可以通过溶度积数据直接比较溶解度大小,不同类型,不可直接比较。
解题的一般步骤
1) 写出化学方程式;
2) 用溶解度 S 表示出平衡浓度;
3) 写出 Ksp 的表达式;
4) 将已知数据代入后,求值或解方程
例1:室温下,AgCl的溶解度是1.93×10-3g/L,求AgCl的溶度积。已知AgCl的摩尔质量为143.3g/mol。
解:
①把AgCl溶解度单位(g/L)换算成mol·L-1
s=1.93×10-3g/L÷143.3g/mol
=1.35×10-5mol·L-1
②求Ksp
AgCl(s) Ag+ + Cl-
饱和、平衡 1.35×10-5 1.35×10-5
Ksp(AgCl)=[Ag+][Cl-]
=(1.35×10-5)2
=1.82×10-10
答:AgCl的Ksp为1.82×10-10
例2:Mg(OH)2的Ksp=1.20×10-11在298K时,Mg(OH)2的溶解度为多少
解:Mg(OH)2(s) Mg2++2OH-
设溶解度为s
平衡时 s 2s
Ksp=[Mg2+][OH-]2
=s(2s)2
=4s3
=1.2×10-11
∴ s=1.44×10-4mol·L-1
答:氢氧化镁在298K时的溶解度为
1.44×10-4mol·L-1。
例3:Ag2CrO4在298K时溶解度s=1.34×10-4mol·L-1求:Ksp
解:
Ag2CrO4(s) 2Ag+ + CrO42-
平衡时 2×1.34×10-4 1.34×10-4
Ksp=[Ag+]2[CrO42-]
=(2×1.34×10-4)2×1.34×10-4
=9.62×10-12
答:铬酸银在298K时的Ksp=9.62×10-12
由以上三个例题的结果可得到如下结论:
①同种类型的难溶电解质,在一定温度下,Ksp越大则溶解度越大。
②不同类型则不能用Ksp的大小来比较溶解度的大小,必须经过换算才能得出结论。
3、溶度积与温度的关系
Kspθ仅与温度有关,和其它平衡常数一样,可用热力学公式进行计算。
3、溶度积规则
离子积
Qi与Ksp区别:
表达式相同
意义不同( Ksp表示饱和溶液,平衡态; Qi表示任意状态)
对于沉淀-溶液平衡:
AmBn mAn+ + nBm-
离子积:某难溶电解质溶液中,其离子浓度系数方之乘积,以Qi表示。
平衡态时:Ksp = [An+ ]m[Bm-]n
任意态时:Qi = Cm(An+ )Cn(Bm-)
—比较任一条件下离子积Qi与Ksp 之间的大小,来判断沉淀的生成和溶解
3、溶度积规则
如:Ag2CrO4
任意情况下的离子积为:
Qi=c2(Ag+)×c(CrO42-)
①当Qi=Ksp
②当Qi ③当Qi>Ksp
无沉淀析出即平衡状态,
是饱和溶液
若有固体则发生溶解,
是不饱和溶液
向生成沉淀的方向移动,
是过饱和溶液
例 在20mL 0.0020mol·L-1Na2SO4溶液中加入 20 mL 0.020mol·L-1 BaCl2溶液,有无BaSO4沉淀生成?并判断 SO42- 离子是否沉淀完全?已知BaSO4的Ksp= 1.07×10-10 .
解:(1)
∴ 有BaSO4沉淀生成
即 1.07×10-10 ≈ 0.0090 x
∴ x = [SO42-] ≈ 1.2×10-8 mol· L-1
⑵ 设平衡时 [SO42-] = x mol·L-1
沉淀完全是指离子残留量 ≤ 10-5 mol· L-1
故加入BaCl2 可使SO42- 沉淀完全
Ksp = [Ba2+][SO42-] = ( 0.0090 + x ) x
起始浓度/mol·L-1 0.010 0.0010
平衡浓度/ mol·L-1 0.010﹣0.0010+x x
BaSO4 (s) Ba 2+ + SO42-
∴ 0.0090 + x ≈ 0.0090
∵ x 很小
同离子效应和盐效应
在饱和BaSO4溶液中存在下列平衡:
BaSO4 (s) Ba2+(aq) + SO42-(aq)
如往溶液中加入含Ba2+或SO42-离子的物质则可以使BaSO4溶解度降低。因此,当溶液中存在与难溶电解质同种的离子时,由于同离子效应,难溶物的溶解度将降低。如加入KNO3等不含有同种离子的强电解质,则可使难溶物的溶解度增大,这一现象叫做盐效应。
4、影响沉淀平衡的因素
组成沉淀晶体的离子称为构晶离子。当沉淀反应达到平衡后,如果向溶液中加入适当过量的含有某一构晶离子的试剂或溶液,则沉淀的溶解度减小,称之为共同离子效应。
同离子效应和盐效应
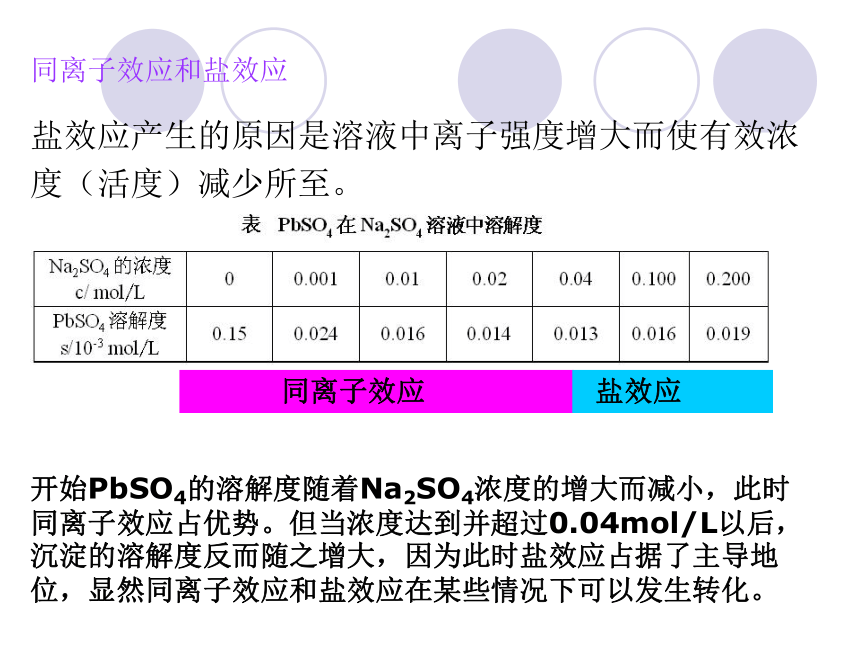
盐效应产生的原因是溶液中离子强度增大而使有效浓度(活度)减少所至。
开始PbSO4的溶解度随着Na2SO4浓度的增大而减小,此时同离子效应占优势。但当浓度达到并超过0.04mol/L以后,沉淀的溶解度反而随之增大,因为此时盐效应占据了主导地位,显然同离子效应和盐效应在某些情况下可以发生转化。
同离子效应
盐效应
同离子效应和盐效应
注:沉淀溶解度很小时,常忽略盐效应。
沉淀溶解度很大,且溶液离子强度很高时,要考虑盐效应的影响。
例:298K时硫酸钡的溶解度为1.04×10-5mol·L-1,如果在0.010mol·L-1的硫酸钠溶液中的溶解度是多少?
解:①先求Ksp
BaSO4 Ba2+ + SO42-
1.04×10-5 1.04×10-5
Ksp=[Ba2+][SO42-]
=1.04×10-5×1.04×10-5
=1.08×10-10
②求s
Na2SO4→2Na+ + SO42-
BaSO4 Ba2+ + SO42-
初 0 0.01
平衡 s s+0.01≈0.01
Ksp=[Ba2+][SO42-]
=s×0.01
s=Ksp/0.01
=1.08×10-10/0.01
=1.08×10-8mol·L-1
s<<0.01,即前面的近似是合理的。
答:溶解度是1.08×10-8mol·L-1。
可见在溶液中离子的浓度不可能为零,当溶液中被沉淀离子浓度小于10-5mol·L-1时即可认为沉淀完全了。
酸效应
溶液酸度对沉淀溶解度的影响称为~
产生酸效应的原因是:因为酸度变化,构晶离子会与溶液中的H+或OH-发生副反应,降低了构晶离子的浓度,使沉淀溶解平衡移向溶解,从而使沉淀溶解度增大
强酸盐的溶解度受酸度影响不显著;
对弱酸盐影响比较明显,组成盐的酸越弱,影响越大。
4、影响沉淀平衡的因素
配位效应
进行沉淀反应时,若溶液中存在能与构晶离子生成可溶性配合物的配位剂、则反应向沉淀溶解的方向进行,影响沉淀的完全程度,甚至不产生沉淀,这种影响称为配位效应。
如在生成AgCl沉淀的溶液中,加入氨水,由于NH3与Ag+形成[Ag(NH3)2]+,而使AgCl的溶解度增大,甚至全部溶解。
AgCl Ag+ +Cl-
2NH3
[Ag(NH3)2]+
4、影响沉淀平衡的因素
影响溶解度的其他因素
1.温度: T↑, S↑(个别反常)
2.溶剂: 相似者相溶, 加入有机溶剂,S↓
3.颗粒大小:小颗粒溶解度大
4.胶体和析出形态
分步沉淀
概念:混合溶液中的离子,由于各种沉淀溶度积的差别而分别先后沉淀的现象。
5、分步沉淀和沉淀转化
例:在含有0.01mol/LKI和0.01mol/LKCl的溶液中,逐滴加入AgNO3溶液,试计算开始生成AgI和AgCl沉淀时所需的AgNO3浓度。
Cl –离子开始沉淀时,I –离子是否已经沉淀完全?
两者开始沉淀所需要的Ag+离子浓度:
对AgCl:
AgI先沉淀
AgCl和AgI一起沉淀时, c(I-)、c(Cl-)和c(Ag+)同时满足AgI和AgCl的溶度积常数表达式,即
——————— = ————— = 1.9 × 106
c(Cl-)/mol·dm-3
1.8×10-10
c(I-)/mol·dm-3
8.5×10-17
将c(Cl-)/mol·dm-3=0.010代入上式,即可求得AgCl开始沉淀时的c(I-):
c(I-)/mol·dm-3 = 0.010/1.9 × 106 = 5.3 × 10-9
这就是说, AgCl开始沉淀时, 已沉淀完全.
沉淀转化
概念:在某一沉淀的溶液中,加入适当的试剂,使之转化为另一沉淀的反应。
一般沉淀转化反应由溶解度较大的难溶电解质转化为溶解度较小的物质,相同类型的沉淀Ksp相差越大,沉淀越易转化
5、分步沉淀和沉淀转化
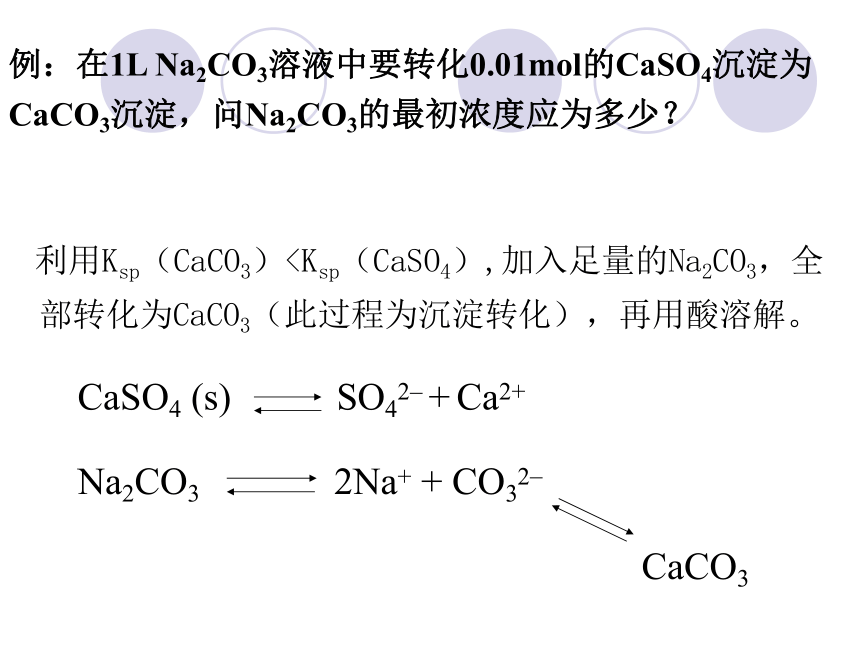
利用Ksp(CaCO3)CaSO4 (s) SO42_ + Ca2+
Na2CO3 2Na+ + CO32_
CaCO3
例:在1L Na2CO3溶液中要转化0.01mol的CaSO4沉淀为CaCO3沉淀,问Na2CO3的最初浓度应为多少?
如上例沉淀转化反应为 :
CaSO4 + CO32_ CaCO3 + SO42_ K转
实际由下列反应组成:
CaSO4 (s) Ca2+ + SO42_ K1=KSP(CaSO4)
Ca2+ + CO32_ CaCO3 K2= 1/KSP(CaCO3 )
根据多重平衡规律:
K转=K1· K2=KSP(CaSO4)/KSP(CaCO3 )
=7.1×10-5/4.6×10-9=1.43×104
这种转化常常被人们利用,如:处理锅垢(含CaSO4),由于CaSO4难溶于酸,利用Na2CO3使之转化为CaCO3。
祝大家新年快乐!
第九章 水溶液中的离子平衡
第九章 水溶液中的离子平衡
一、酸碱平衡
二、配离子平衡
三、难溶电解质的离子平衡
电解质和非电解质
强电解质和弱电解质
温故而知新
Fe
CO2
SO2
Al2O3
CaCO3
SO3
H2SO4
H2O
NH3·H2O
H2SO3
NaCl
NaHSO4
C2H5OH
NH3
电解质
非电解质
Fe
Fe
NaCl
NaHSO4
H2SO4
SO2
CO2
Al2O3
NH3·H2O
CaCO3
C2H5OH
H2SO3
SO3
NH3
H2O
能导电的物质一定是电解质?
不导电的物质一定是非电解质?
第九章 水溶液中的离子平衡
一、酸碱平衡
1.掌握解离度、解离常数、共轭酸碱对、缓冲溶液、同离子效应等基本概念
2.掌握酸碱质子理论、酸碱反应的实质、质子自递反应、共轭酸碱对的解离常数的关系
3.掌握强酸碱溶液、弱酸碱溶液、缓冲溶液的H+浓度的计算。
1、电解质溶液的通性
从部分电解质的0.1mol·kg-1溶液的凝固点下降数值与理论值的比较可以得到电解质溶液的偏差 i 值
电解质 实测ΔT’f / K 计算Δ Tf / K i= ΔT’f / Δ Tf
NaCl 0.348 0.186 1.87
HCl 0.355 0.186 1.91
K2SO4 0.458 0.186 2.46
CH3COOH 0.188 0.186 1.01
可以看出,产生的偏差有以下规律:
A2B(AB2)强电解质>AB强电解质>AB弱电解质>非电解质
一、酸碱平衡
稀溶液的依数性?
1、电解质溶液的通性
阿仑尼乌斯根据电解质溶液不服从稀溶液依数性的现象,提出了电离理论。
电离理论认为电解质分子在水溶液中解离
成离子,使得溶液中的微粒数增大,故它们的蒸汽压、沸点、熔点的改变和渗透压数值都比非电解质大。
为什么溶液的蒸气压会下降?
当溶质分散于溶剂之中,溶液表面的部分位置被溶质的粒子所占据,使得单位表面所能逸出的溶剂的分子个数减少,因此溶液蒸气压较之纯溶剂有所降底。
1、电解质溶液的通性
解离度——
溶液中已解离的电解质的分子数与电解质总分子数之比。
2、水溶液中的单相离子平衡
水溶液中的单相离子平衡一般分为酸、碱的解离平衡及配离子的解离平衡两类。
根据解离度的大小,将电解质分为:
强电解质和弱电解质两类。
强电解质在水中全部解离,而弱电解质在水溶液中只有部分解离,大部分仍以分子形式存在。弱电解质在水溶液中存在解离平衡。
强电解质
弱电解质
H2SO4
CaCO3
Ca(OH)2
Fe(OH)3
H2CO3
NaHCO3
NH3·H2O
C12H22O11
按先后次序,酸碱理论主要有以下几种:
a.酸碱电离理论(阿氏水离子论)
在水溶液中解离时所生成的正离子全部是H+的化合物是酸;所生成的负离子全部是OHˉ的化合物是碱。
酸碱中和反应的实质是H+ + OHˉ = H2O。
酸碱电离理论的缺陷:
把酸、碱的定义局限于以水为溶剂的系统。
无法解释NH3、Na2CO3均不含OHˉ,也具有碱性。
3、酸碱的概念
b.酸碱质子理论
凡能给出质子的物质都是酸;
凡能结合质子的物质都是碱。
在水溶液中
HCl(aq)= H+(aq) +Cl-(aq)
HAc(aq) H+(aq) +Acˉ(aq)
NH4+(aq) H+(aq) +NH3(aq)
HCO3-(aq) H+(aq) + CO32-(aq)
酸 质子 + 碱
b.酸碱质子理论
在水溶液中
HCl(aq)= H+(aq) +Cl-(aq)
HAc(aq) H+(aq) +Acˉ(aq)
NH4+(aq) H+(aq) +NH3(aq)
HCO3-(aq) H+(aq) + CO32-(aq)
酸、碱可以是分子,也可以是离子。
酸给出质子后可以再结合质子,因此酸给出质子后就变为碱:
酸 质子 + 碱
(质子给予体) (质子接受体)
b.酸碱质子理论
共轭酸碱概念
酸与对应的碱的这种相互依存、相互转化的关系称为酸碱共轭关系。
酸失去质子后形成的碱被称为该酸的共轭碱;碱结合质子后形成的酸被称为该碱的共轭酸。
共轭酸与它的共轭碱一起称为共轭酸碱对。例如:
(1)
a.因一个质子的得失而互相转变的每一对酸和碱,称为共轭酸碱对(如:HAc-Ac-),彼此相差一个H+。
b.酸碱的定义是广义的,酸碱可以是分子,也可以是阳离子、阴离子。
c.酸碱具有相对性。既可失去质子、又可得到质子的物质,称为两性物质。如:HCO3-、HPO4-等。
酸
碱半
反
应
b.酸碱质子理论
酸碱反应 是两对共轭酸碱对共同作用的结果。
共轭酸碱对
HAc + H2O H3O+ +Ac- (电离)
H3O+ +NH3 H2O+ NH4 (中和)
H2O+ CN- OH- + HCN (水解)
H2O+ CO3 HCO3 + OHˉ(水解)
2-
–
+
b.酸碱质子理论
酸碱反应 是两对共轭酸碱对共同作用的结果。
共轭酸碱对
HAc + H2O H3O+ +Ac- (电离) HAc/Ac-, H3O+/ H2O
H3O+ +NH3 H2O+ NH4 (中和) NH4 /NH3, H3O+/ H2O
H2O+ CN- OH- + HCN (水解) HCN/CN-, H2O/OH-
H2O+ CO3 HCO3 + OHˉ(水解) HCO 3/CO3, H2O/OH-
2-
–
+
+
–
2-
酸碱反应 是两对共轭酸碱对共同作用的结果。
H+就是一个原子核,光秃秃,半径小,又带正电荷,所以不能以游离状态存在, H+在水中的平均寿命只有10-14s。所以, H+一出现便立即附着于溶剂分子上,产生一种酸。
例如: H+ + H2O = H3O+
H+
为了书写方便,总反应可写成:
HAc=H++Ac-
注意,它代表的是总反应,不能忽略H2O起的作用。
HAc-Ac-
H3O+-H2O
H2O为碱
同理:
H+
可见:H2O是两性物质
H2O-OH-
NH4+-NH3
H2O为酸
又如HCl与NH3的反应:
H+
NH4+-NH3
HCl-Cl-
质子自递反应
H+
H2O-OH-
H3O+-H2O
水的质子自递常数(离子积):
纯溶液的浓度视为1,
pKw=pH+pOH=14
b.酸碱质子理论
酸碱质子理论扩大了酸碱的范围,它比电离理论更广泛,其酸碱的定义只以H+为判据,与溶剂无关,可以解释NH3、Na2CO3以及NH4Cl等的酸碱性。
两性物质: H2O, HCO3ˉ (所有酸式根)
无盐的概念: NH4Cl (酸碱复合物)
酸碱质子理论是概念的一场革新:
C.酸碱电子理论
凡能接受电子对的物质是酸,凡能给出电子对的物质是碱,也称为路易斯酸碱理论。
A+ B= A B
H+ + OH- = H2O
酸 + 碱 = 酸碱加合物
(1) H3BO3 + H2O [B(OH)4]ˉ + H+ (硼酸是路易斯酸)
Cu2+ + 4NH3 [Cu(NH3)4]2+ 深蓝色
酸 碱 加合物
酸碱电子理论摆脱了酸必须含有H的限制,包括的范围更广。
4、酸碱的强度
(一) 一元酸碱的强度
HA + H2O H3O+ + A-
酸度常数
(酸的解离常数)
A-+ H2O OH- + HA
碱度常数
(碱的解离常数)
讨论:
Ka↑,给质子能力↑强,酸的强度↑
Kb↑,得质子能力↑强,碱的强度↑
共轭酸碱对HA和A- 有如下关系
酸愈强,其共轭碱必定愈弱。
续
(二)多元酸碱的强度
H3PO4 H2PO4 - + H+
Ka1 Kb3
H2PO4- HPO42- + H+
Ka2 Kb2
HPO42- PO43- + H+
Ka3 Kb1
讨论:
多元酸碱在水中逐级离解,强度逐级递减
形成的多元共轭酸碱对中最强酸的解离常数
Ka1对应最弱共轭碱的解离常数Kb3
强酸强碱溶液pH值的计算
强酸(Ca )
HA H + + A -
H2O H + + OH -
当Ca > 10-6 mol/L,忽略水的解离
精确式
近似式***
5、酸碱溶液pH计算
当Ca < 10-8 mol/L, pH≈7
=
由水电离出的氢离子浓度和氢氧根离子浓度始终相等,不仅限于纯水中,对任何水溶液都成立。
续强酸强碱pH值计算
强碱(Cb )
精确式
B + H + BH +
H2O H + + OH –
近似式***
=
当Cb> 10-6 mol/L,忽略水的解离
一元弱酸和一元弱碱pH值的计算
设一元弱酸HA的浓度为c, 解离度为α
HA H+ + A-
起始浓度 c 0 0
平衡浓度 c(1-α) cα cα
因此
同理,对于一元弱碱:
溶液的酸度(H+离子浓度)常用pH表示, pH = –lg{c(H+)/c }, 溶液的碱度(OHˉ离子浓度)可用pOH表示。
当Kac≥20Kw, c/Ka≥500时,
例题
附例3.1 已知HAc的Ka =1.76×10-5,计算3.0%米醋(含HAc浓度为0.50 mol·dm-3)的pH。
解:设米醋溶液中H+的平衡浓度为x mol·dm-3, 则
HAc(aq) = H+(aq) + Ac-(aq)
平衡浓度/mol·dm-3 0.50 – x x x
Ka = 1.76×10-5
∵ c / Ka > 500 ∴ x很小,0.50 – x ≈ 0.5
pH = –lg c( H+)/c = –lg(2.97×10-3) = 3 – 0.47 = 2.53
例题
例3.2 计算0.100 mol·dm-3 NH4Cl溶液中H+浓度及其pH。
解: NH4Cl(aq) = NH4+(aq) + Clˉ(aq)
NH4+(aq) + H2O(l) = NH3(aq) + H3O+ (aq)
Ka =5.65×10-10
pH = – lg c( H+)/c = –lg(7.52×10-6) = 5.12
多元弱酸和多元弱碱pH值的计算
多元弱酸(碱)的解离是分级进行的,每一级解离都有一个解离常数,以磷酸为例:
一级解离:
二级解离:
三级解离:
说明
式中,Ka,3 << K a,2 << K a,1,每级解离常数差3~6个数量级。
因此, H+浓度的计算以一级解离为主。
计算H+浓度时,当Ka,2 / K a,1<10ˉ3时,可忽略二、三级解离平衡。
比较多元弱酸的酸性强弱时,只需比较它们一级解离常数值即可。
思考:根据反应式 H2S(aq) = 2H+(aq) + S2ˉ ,H+浓度是S2ˉ 离子浓度的两倍,此结论是否正确?
是错误的, H2S(aq)以一级电离为主,因此H2S溶液中c(H+) ≈ c(HSˉ)。
-
例题
附例3.3 已知 H2CO3的 Ka,1= 4.30×10-7, K a,2 = 5.61×10-11, 计算0.0200 mol·dm-3 H2CO3溶液中H+和 的浓度及pH。
解:∵Ka,2<
H2CO3 H+ + HCO3 HCO3 H+ + CO32
第一步解离生成的H+抑制了第二步解离,因此 c(H+) ≈ c (HCO3 ) ≈ 9.27×10-5 mol·dm-3
c (CO32 ) = Ka,2 = 5.61×10-11 mol·dm-3
两性物质溶液pH值的计算
NaHA
Na H2PO4
Na2HPO4
缓冲溶液和pH的控制
同离子效应
在弱酸的溶液中加入该酸的共轭碱,或在弱碱的溶液中加入该碱的共轭酸
如HAc的水溶液中,
HAc(aq) = H+(aq) + Ac-(aq)
由于NaAc = Na++Acˉ
使得HAc解离平衡向左移动,HAc的解离度降低。
在弱酸的溶液中加入该酸的共轭碱,或在弱碱的溶液中加入该碱的共轭酸,使得弱酸或弱碱的解离度大大下降的现象,称为同离子效应。
加入NaAc,
例题
例3.3 在0.100 mol·dm-3HAc溶液中加入一定量固体NaAc,使NaAc的浓度等于0.100 mol·dm-3,求该溶液中H+浓度,pH和HAc的解离度α。
解:设已解离的HAc的浓度为x mol·dm-3
HAc = H+ + Ac
平衡浓度/mol·dm-3 0.1–x x 0.1+x
c(H+) = x mol·dm-3= 1.76 ×10-5 mol·dm-3, pH = 4.75
与例3.1相比,同离子效应使αHAc从1.34%降为0.018%, c(H+)从1.34 ×10-3 mol·dm-3 减少到1.76 ×10-5 mol·dm-3。
缓冲溶液
弱酸及其共轭碱或弱碱及其共轭酸所组成的溶液具有一个重要性质,该溶液的pH在一定范围内不因稀释或外加少量酸或碱而发生显著变化,即对外加的酸和碱具有缓冲能力,这种溶液称作缓冲溶液。
以HAc和NaAc的混合溶液为例:
NaAc == Na++ Ac-
HAc(aq) = H+(aq) + Ac-(aq)
系统中大量HAc、Acˉ存在,使H+相对较少。当溶液中加入少量强酸时,H+与Acˉ结合生成HAc,使H+的浓度保持基本不变。
若往系统中加入少量强碱,则H+与OH-结合生成H2O,使HAc解离平衡右移, HAc的浓度减少,而H+的浓度仍保持基本不变。
缓冲溶液的pH
当加入大量的强酸或强碱,使溶液中的Ac 或HAc耗尽,则溶液将失去缓冲能力。
组成缓冲溶液的一对共轭酸碱,如HAc–Ac 又称为缓冲对。可用通式表示缓冲对之间存在的平衡:
共轭酸 = 共轭碱 + H+
例题
附例3.4 40.00 cm3 1.00mol·dm-3 HAc与20.00cm3 1.00mol·dm-3 NaOH混合,求混合液的pH
解:HAc + NaOH = NaAc + H2O
由于HAc过量,反应平衡后生成0.02mol的Acˉ,并剩余0.02mol HAc,溶液总体积为60.00cm3。于是
已知HAc的pKa为4.76
因此
例题
解:50.00cm3缓冲溶液中加入盐酸后总体积为50.05 cm3,加入的1.000 mol·dm 3盐酸由于稀释,浓度变为:
由于加入的H+的量相对于溶液中Acˉ的量而言很小,可认为加入的H+完全与Acˉ结合成HAc分子。于是
c(HAc) = (0.1000 + 0.001)mol ·dm 3 = 0.101 mol ·dm 3,
c(Acˉ) = (0.1000 – 0.001)mol ·dm 3 = 0.099 mol ·dm 3
附例3.5 已知若在 50.00 cm3 含有 0.1000 mol·dm 3的HAc 和0.1000 mol·dm 3 NaAc缓冲液中,加入0.050 cm3 1.000 mol·dm 3 盐酸,求其pH。
说明
计算结果表明,50 cm3 HAc-NaAc缓冲溶液中,若加入少量的强酸(0.05cm3 1.0mol·dm-3的盐酸),溶液的pH由4.76降至4.74,仅改变0.02;但若在50cm3纯水中加入0.05cm3 1.0 mol·dm-3 HCl 溶液,则由于H+的浓度约为0.001mol·dm-3,pH等于3。即pH改变了4个单位。
思考:缓冲溶液的缓冲能力与哪些因素有关?
缓冲能力主要与以下因素有关:
缓冲溶液中共轭酸的pKa值:缓冲溶液的pH在其pKa值附近时,缓冲能力最大。
缓冲对的浓度:缓冲对的浓度均较大时,缓冲能力较大。
缓冲对的浓度比: 为1:1或相近(0.1~10)时,缓冲能力较大。
缓冲溶液的选择和配制
据所需pH选择缓冲对
缓冲溶液的pH不仅取决于缓冲对中共轭酸的Ka,还取决于缓冲对中两种物质浓度的比值。缓冲对中任一物质的浓度过小都会使溶液丧失缓冲能力,故两者浓度之比最好趋近于1,此时缓冲能力最强。
当c(共轭酸) = c(共轭碱)时,pH = pKa
因此选择缓冲体系时,应选择共轭酸的pKa与要求的pH相近的缓冲对。
一般认为,当缓冲对的浓度比在0.1和10之间才具有缓冲作用,因此,缓冲溶液的pH 和pKa之间有以下关系:
pH = pKa ± 1
常用缓冲溶液
缓冲溶液 共轭酸碱对 pKa 缓冲范围
HCO2H/NaOH HCO2H -HCO2– 3.75 2.75~4.75
CH3CO2H/CH3CO2Na HAc -Ac – 4.75 3.75~5.75
NaH2PO4/Na2HPO4 H2PO4 -HPO42– 7.21 6.21~8.21
NH3·H2O /NH4Cl NH4+ - NH3 9.25 8.25~10.25
NaHCO3/Na2CO3 HCO3– - CO32– 10.25 9.25~11.25
Na2HPO4 /NaOH HPO4 2– - PO43– 12.66 11.66~13.66
常用缓冲溶液的缓冲范围
例题
附例3.6: 要配制10cm3 pH=5的HAc-NaAc缓冲液,问需浓度为1.0 mol·dm-3的HAc和NaAc溶液各多少毫升?
由于两者浓度相同,因此只需体积比和总体积满足:
V(HAc)/V(NaAc)=0.562 又V(HAc) + V(NaAc) = 10cm3
因此:V(HAc) = 3.6 cm3;V(NaAc) = 6.4 cm3
解:
练习
1. 已知0.1000mol/L HA溶液的pH=3,计算同浓度NaA溶液的pH值
解:
练习
3.某缓冲溶液100mL,HA的浓度为0.25mol/L(pKa=5.3),于此溶液中加入0.2g的NaOH(忽略体积变化)后,pH=5.6,问该缓冲溶 液原来的pH值是多少?
解:
练习
1、H2O的共轭酸是 ( )
A. H2O B. HAc C. H3O+ D. OH-
C
2、根据酸碱质子理论,正确的说法是 ( )
A. 酸愈强,则其共轭碱愈弱
B. H3O+是水溶液中的最强酸
C. H3O+的共轭碱是OH-
D. OH-是水溶液中的最强碱
A、B、D
3、根据酸碱质子理论下列化合物中不属于酸的是 ( )
A. HCO3- B. NH4+ C. HAc D. Ac-
D
1.稳定常数和不稳定常数
解离
配合
—— 配合(位)平衡
1)不稳定常数
二、配离子平衡
2)稳定常数
生成配合物的反应是配合物解离反应的逆反应。
越大,则配合物越稳定
3)逐级稳定常数
4)累积稳定常数 ( β )
β 为各级配离子的稳定常数
2.稳定常数的应用
已知配位单元的浓度,利用标准稳定常数或标准不稳定常数可以计算配体和中心原子的平衡浓度。
(1)计算配位平衡的组成
例 计算0.10 mol·L-1[Ag(NH3) 2]+溶液中的Ag+
和 NH3 的浓度。
解:设溶液中Ag+的平衡浓度为 x mol·L-1,则有:
c0 /mol·L-1 0.10 0 0
c/mol·L-1 -x +x +2x
ceq/mol·L-1 0.10-x x 2x
标准平衡常数表达式为:
代入数据得:
由于 很小,因此 x 很小,可近似认为0.10-x=0.10 。由上式得:
解得:
溶液中 Ag+ 和 NH3 的平衡浓度分别为:
例 在 10.0 mL 0.040 mol·L-1 AgNO3 溶液中加
入10.0mL 2.0 mol·L-1 NH3 溶液,计算平衡溶液中配
体、中心原子和配位离子的浓度。
解:两种溶液混合后,Ag+ 和 NH3 的起始浓度为:
由于 NH3 过量,且 很大,可假定
Ag+全部生成 。再设平衡时
解离出的 Ag+ 浓度为 x mol·L-1,则:
ceq/mol·L-1
标准平衡常数表达式为:
代入数据得:
x =1.4×10-9
2.稳定常数的应用
(2) 判断配位反应进行的方向
在一种配位化合物的溶液中,加入另一种配体或中心原子,它也能与配位单元中的中心原子或配体发生配位反应,形成新的配位单元。利用标准平衡常数就可以判断反应进行的方向。如果配位反应的标准平衡常数很大,且加入的配体或中心原子的浓度足够大,则配位反应正向进行。
解:可能发生的反应:
[例题] 向含有 的溶液中加入KCN,
能否转化为
上述配位反应的标准平衡常数为:
K很大,配位反应向生成 [Ag(CN) 2]- 的正反应方向进行。若加入足量的 CN-,[Ag(NH3) 2]+ 可全部转化成 [Ag(CN) 2]-。
2.稳定常数的应用
(3)判断配离子与沉淀之间转化的可能性
一些难溶强电解质往往因形成配离子而溶解。利用配离子的标准稳定常数或标准不稳定常数,可以计算难溶电解质在有配体存在时的溶解度及全部转化为配离子时所需配体的浓度。
(4)配合物的生成对电极电势的影响
三、难溶电解质的离子平衡
难溶性物质一般是指在 100 克水中溶解的量少于 0.01 克的物质。但是有些物质并不符合这个标准,例如: PbCl2 CaSO4 HgSO4 g/100g H2O 0.675 0.176 0.055 由于这些物质的式量很大,所以其饱和溶液的物质的量浓度相当小,故这些化合物仍作为难溶性化合物讨论
讨论的对象是难溶性强电解质。
1、溶度积常数
沉淀-溶解平衡是当溶解和结晶速度相等时建立的平衡,是一种动态平衡。
此时的溶液是饱和溶液,它是多相平衡。其平衡关系为:
AgCl(s) Ag+ + Cl-
Ksp(AgCl) = [Ag+][Cl_]
KSP称为溶度积常数,简称溶度积。它反应了物质的溶解能力。
溶解
沉淀
难溶电解质溶度积常数通式:
AmBn mAn+ + nBm-
Ksp = [An+]m[Bm-]n
m、n分别代表电离方程式中A、B离子的化学计量数。
溶度积常数的意义:一定温度下,难溶强电解质饱和溶液中离子浓度的系数次方之积为一常数。
Ksp越大则难溶电解质在溶液中溶解趋势越大,反之越小。
例如:PbCl2(s) Pb2+(aq) + 2Cl-(aq) ;
Ksp=[Pb2+][Cl-]2
Fe(OH)3 Fe3+ + 3OH- ;
Ksp=[Fe3+][OH]3
2、溶度积与溶解度的关系
溶度积与溶解度都可表示物质的溶解能力,但它们既有区别又有联系。
一定温度下饱和溶液的浓度,也就是该溶质在此温度下的溶解度。溶质的溶解度为S,单位为mol.l-1,那么:
对于MA型的沉淀
对于MmAn型的沉淀,其溶解平衡关系式:
设MmAn的溶解度为s,即
如:已知AgCl、Ag2CrO4的溶度积,求AgCl、Ag2CrO4的溶解度。
AgCl(s) Ag+ + Cl-
S S
Ksp = [Ag+][Cl-] = S2 = 1.8*10-10
SAgCl = Ksp = 1.8*10-10
= 1.3*10-5mol.l-1
上式为AB型(1:1)溶解度计算式,同理可导出AB2和A2B型:
SAg2CrO4= =
=6.5*10-5mol.l-1
相同类型的电解质,可以通过溶度积数据直接比较溶解度大小,不同类型,不可直接比较。
解题的一般步骤
1) 写出化学方程式;
2) 用溶解度 S 表示出平衡浓度;
3) 写出 Ksp 的表达式;
4) 将已知数据代入后,求值或解方程
例1:室温下,AgCl的溶解度是1.93×10-3g/L,求AgCl的溶度积。已知AgCl的摩尔质量为143.3g/mol。
解:
①把AgCl溶解度单位(g/L)换算成mol·L-1
s=1.93×10-3g/L÷143.3g/mol
=1.35×10-5mol·L-1
②求Ksp
AgCl(s) Ag+ + Cl-
饱和、平衡 1.35×10-5 1.35×10-5
Ksp(AgCl)=[Ag+][Cl-]
=(1.35×10-5)2
=1.82×10-10
答:AgCl的Ksp为1.82×10-10
例2:Mg(OH)2的Ksp=1.20×10-11在298K时,Mg(OH)2的溶解度为多少
解:Mg(OH)2(s) Mg2++2OH-
设溶解度为s
平衡时 s 2s
Ksp=[Mg2+][OH-]2
=s(2s)2
=4s3
=1.2×10-11
∴ s=1.44×10-4mol·L-1
答:氢氧化镁在298K时的溶解度为
1.44×10-4mol·L-1。
例3:Ag2CrO4在298K时溶解度s=1.34×10-4mol·L-1求:Ksp
解:
Ag2CrO4(s) 2Ag+ + CrO42-
平衡时 2×1.34×10-4 1.34×10-4
Ksp=[Ag+]2[CrO42-]
=(2×1.34×10-4)2×1.34×10-4
=9.62×10-12
答:铬酸银在298K时的Ksp=9.62×10-12
由以上三个例题的结果可得到如下结论:
①同种类型的难溶电解质,在一定温度下,Ksp越大则溶解度越大。
②不同类型则不能用Ksp的大小来比较溶解度的大小,必须经过换算才能得出结论。
3、溶度积与温度的关系
Kspθ仅与温度有关,和其它平衡常数一样,可用热力学公式进行计算。
3、溶度积规则
离子积
Qi与Ksp区别:
表达式相同
意义不同( Ksp表示饱和溶液,平衡态; Qi表示任意状态)
对于沉淀-溶液平衡:
AmBn mAn+ + nBm-
离子积:某难溶电解质溶液中,其离子浓度系数方之乘积,以Qi表示。
平衡态时:Ksp = [An+ ]m[Bm-]n
任意态时:Qi = Cm(An+ )Cn(Bm-)
—比较任一条件下离子积Qi与Ksp 之间的大小,来判断沉淀的生成和溶解
3、溶度积规则
如:Ag2CrO4
任意情况下的离子积为:
Qi=c2(Ag+)×c(CrO42-)
①当Qi=Ksp
②当Qi
无沉淀析出即平衡状态,
是饱和溶液
若有固体则发生溶解,
是不饱和溶液
向生成沉淀的方向移动,
是过饱和溶液
例 在20mL 0.0020mol·L-1Na2SO4溶液中加入 20 mL 0.020mol·L-1 BaCl2溶液,有无BaSO4沉淀生成?并判断 SO42- 离子是否沉淀完全?已知BaSO4的Ksp= 1.07×10-10 .
解:(1)
∴ 有BaSO4沉淀生成
即 1.07×10-10 ≈ 0.0090 x
∴ x = [SO42-] ≈ 1.2×10-8 mol· L-1
⑵ 设平衡时 [SO42-] = x mol·L-1
沉淀完全是指离子残留量 ≤ 10-5 mol· L-1
故加入BaCl2 可使SO42- 沉淀完全
Ksp = [Ba2+][SO42-] = ( 0.0090 + x ) x
起始浓度/mol·L-1 0.010 0.0010
平衡浓度/ mol·L-1 0.010﹣0.0010+x x
BaSO4 (s) Ba 2+ + SO42-
∴ 0.0090 + x ≈ 0.0090
∵ x 很小
同离子效应和盐效应
在饱和BaSO4溶液中存在下列平衡:
BaSO4 (s) Ba2+(aq) + SO42-(aq)
如往溶液中加入含Ba2+或SO42-离子的物质则可以使BaSO4溶解度降低。因此,当溶液中存在与难溶电解质同种的离子时,由于同离子效应,难溶物的溶解度将降低。如加入KNO3等不含有同种离子的强电解质,则可使难溶物的溶解度增大,这一现象叫做盐效应。
4、影响沉淀平衡的因素
组成沉淀晶体的离子称为构晶离子。当沉淀反应达到平衡后,如果向溶液中加入适当过量的含有某一构晶离子的试剂或溶液,则沉淀的溶解度减小,称之为共同离子效应。
同离子效应和盐效应
盐效应产生的原因是溶液中离子强度增大而使有效浓度(活度)减少所至。
开始PbSO4的溶解度随着Na2SO4浓度的增大而减小,此时同离子效应占优势。但当浓度达到并超过0.04mol/L以后,沉淀的溶解度反而随之增大,因为此时盐效应占据了主导地位,显然同离子效应和盐效应在某些情况下可以发生转化。
同离子效应
盐效应
同离子效应和盐效应
注:沉淀溶解度很小时,常忽略盐效应。
沉淀溶解度很大,且溶液离子强度很高时,要考虑盐效应的影响。
例:298K时硫酸钡的溶解度为1.04×10-5mol·L-1,如果在0.010mol·L-1的硫酸钠溶液中的溶解度是多少?
解:①先求Ksp
BaSO4 Ba2+ + SO42-
1.04×10-5 1.04×10-5
Ksp=[Ba2+][SO42-]
=1.04×10-5×1.04×10-5
=1.08×10-10
②求s
Na2SO4→2Na+ + SO42-
BaSO4 Ba2+ + SO42-
初 0 0.01
平衡 s s+0.01≈0.01
Ksp=[Ba2+][SO42-]
=s×0.01
s=Ksp/0.01
=1.08×10-10/0.01
=1.08×10-8mol·L-1
s<<0.01,即前面的近似是合理的。
答:溶解度是1.08×10-8mol·L-1。
可见在溶液中离子的浓度不可能为零,当溶液中被沉淀离子浓度小于10-5mol·L-1时即可认为沉淀完全了。
酸效应
溶液酸度对沉淀溶解度的影响称为~
产生酸效应的原因是:因为酸度变化,构晶离子会与溶液中的H+或OH-发生副反应,降低了构晶离子的浓度,使沉淀溶解平衡移向溶解,从而使沉淀溶解度增大
强酸盐的溶解度受酸度影响不显著;
对弱酸盐影响比较明显,组成盐的酸越弱,影响越大。
4、影响沉淀平衡的因素
配位效应
进行沉淀反应时,若溶液中存在能与构晶离子生成可溶性配合物的配位剂、则反应向沉淀溶解的方向进行,影响沉淀的完全程度,甚至不产生沉淀,这种影响称为配位效应。
如在生成AgCl沉淀的溶液中,加入氨水,由于NH3与Ag+形成[Ag(NH3)2]+,而使AgCl的溶解度增大,甚至全部溶解。
AgCl Ag+ +Cl-
2NH3
[Ag(NH3)2]+
4、影响沉淀平衡的因素
影响溶解度的其他因素
1.温度: T↑, S↑(个别反常)
2.溶剂: 相似者相溶, 加入有机溶剂,S↓
3.颗粒大小:小颗粒溶解度大
4.胶体和析出形态
分步沉淀
概念:混合溶液中的离子,由于各种沉淀溶度积的差别而分别先后沉淀的现象。
5、分步沉淀和沉淀转化
例:在含有0.01mol/LKI和0.01mol/LKCl的溶液中,逐滴加入AgNO3溶液,试计算开始生成AgI和AgCl沉淀时所需的AgNO3浓度。
Cl –离子开始沉淀时,I –离子是否已经沉淀完全?
两者开始沉淀所需要的Ag+离子浓度:
对AgCl:
AgI先沉淀
AgCl和AgI一起沉淀时, c(I-)、c(Cl-)和c(Ag+)同时满足AgI和AgCl的溶度积常数表达式,即
——————— = ————— = 1.9 × 106
c(Cl-)/mol·dm-3
1.8×10-10
c(I-)/mol·dm-3
8.5×10-17
将c(Cl-)/mol·dm-3=0.010代入上式,即可求得AgCl开始沉淀时的c(I-):
c(I-)/mol·dm-3 = 0.010/1.9 × 106 = 5.3 × 10-9
这就是说, AgCl开始沉淀时, 已沉淀完全.
沉淀转化
概念:在某一沉淀的溶液中,加入适当的试剂,使之转化为另一沉淀的反应。
一般沉淀转化反应由溶解度较大的难溶电解质转化为溶解度较小的物质,相同类型的沉淀Ksp相差越大,沉淀越易转化
5、分步沉淀和沉淀转化
利用Ksp(CaCO3)
Na2CO3 2Na+ + CO32_
CaCO3
例:在1L Na2CO3溶液中要转化0.01mol的CaSO4沉淀为CaCO3沉淀,问Na2CO3的最初浓度应为多少?
如上例沉淀转化反应为 :
CaSO4 + CO32_ CaCO3 + SO42_ K转
实际由下列反应组成:
CaSO4 (s) Ca2+ + SO42_ K1=KSP(CaSO4)
Ca2+ + CO32_ CaCO3 K2= 1/KSP(CaCO3 )
根据多重平衡规律:
K转=K1· K2=KSP(CaSO4)/KSP(CaCO3 )
=7.1×10-5/4.6×10-9=1.43×104
这种转化常常被人们利用,如:处理锅垢(含CaSO4),由于CaSO4难溶于酸,利用Na2CO3使之转化为CaCO3。
