2020---2021学年人教版七年级下学期期末考试:5.3平行线的性质强化训练(Word版 含答案)
文档属性
| 名称 | 2020---2021学年人教版七年级下学期期末考试:5.3平行线的性质强化训练(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 331.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 11:46:26 | ||
图片预览



文档简介
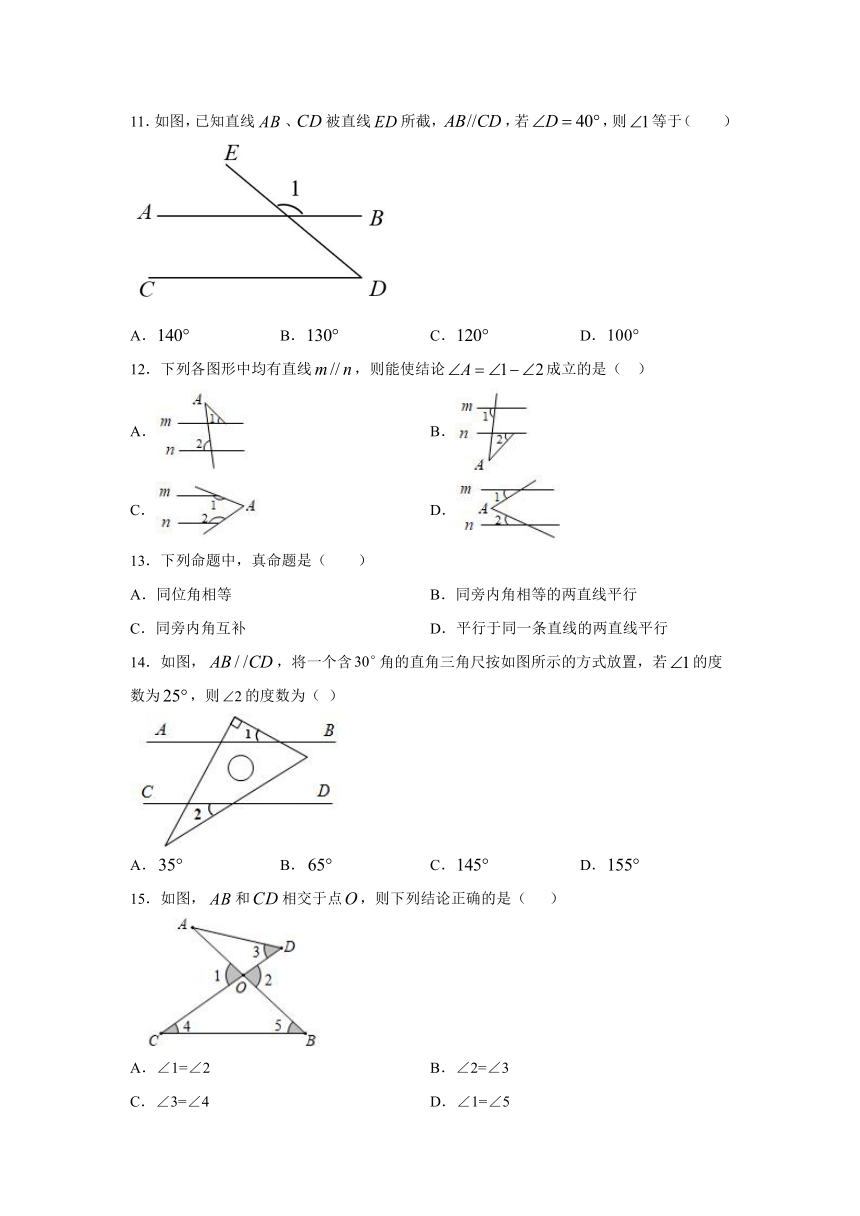
5.3平行线的性质强化训练
一、单选题
1.把命题“同角的余角相等”改写成“如果……那么……”的形式,正确的是(
)
A.如果是同角,那么余角相等
B.如果两个角相等,那么这两个角是同一个角的余角
C.如果是同角的余角,那么相等
D.如果两个角是同一个角的余角,那么这两个角相等
2.如图,已知直线被直线l所截,,若,则的度数是(
)
A.
B.
C.
D.
3.一把直尺和一个含,角的三角板如图所示摆放,直尺一边与三角板的两直角边分别交于,两点,另一边与三角板的两直角边分别交于,两点,且,那么的大小为(
)
A.
B.
C.
D.
4.下列命题与它的逆命题均为真命题的是()
A.内错角相等
B.对顶角相等
C.如果ab0,那么a0
D.互为相反数的两个数和为0
5.下列命题是定理的是(
)
A.内错角相等
B.同位角相等,两直线平行
C.一个角的余角不等于它本身
D.在同一平面内,有且只有一条直线与已知直线垂直
6.下列语句中,不是命题的是( )
A.如果a+b=0,那么a、b互为相反数
B.内错角相等
C.已知a2=4,a的值是多少?
D.负数大于正数
7.如图,已知直线a
//
b
//
c,直线d与它们分别垂直且相交于A,B,C三点,若AB=2,AC=6,则平行线b、c之间的距离是(
)
A.2
B.4
C.6
D.8
8.如图所示,下列推理及括号中所注明的推理依据错误的是(
)
A.,(内错角相等,两直线平行)
B.,(两直线平行,同旁内角互补)
C.,(两直线平行,同旁内角互补)
D.,(同位角相等,两直线平行)
9.如图,已知平分,则的度数是(
)
A.
B.
C.
D.
10.光线在不同介质中的传播速度不同,因此当光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,当∠1=45°,∠2=122°时,∠3和∠4的度数分别是(
)
A.58°,122°
B.45°,68°
C.45°,58°
D.45°,45°
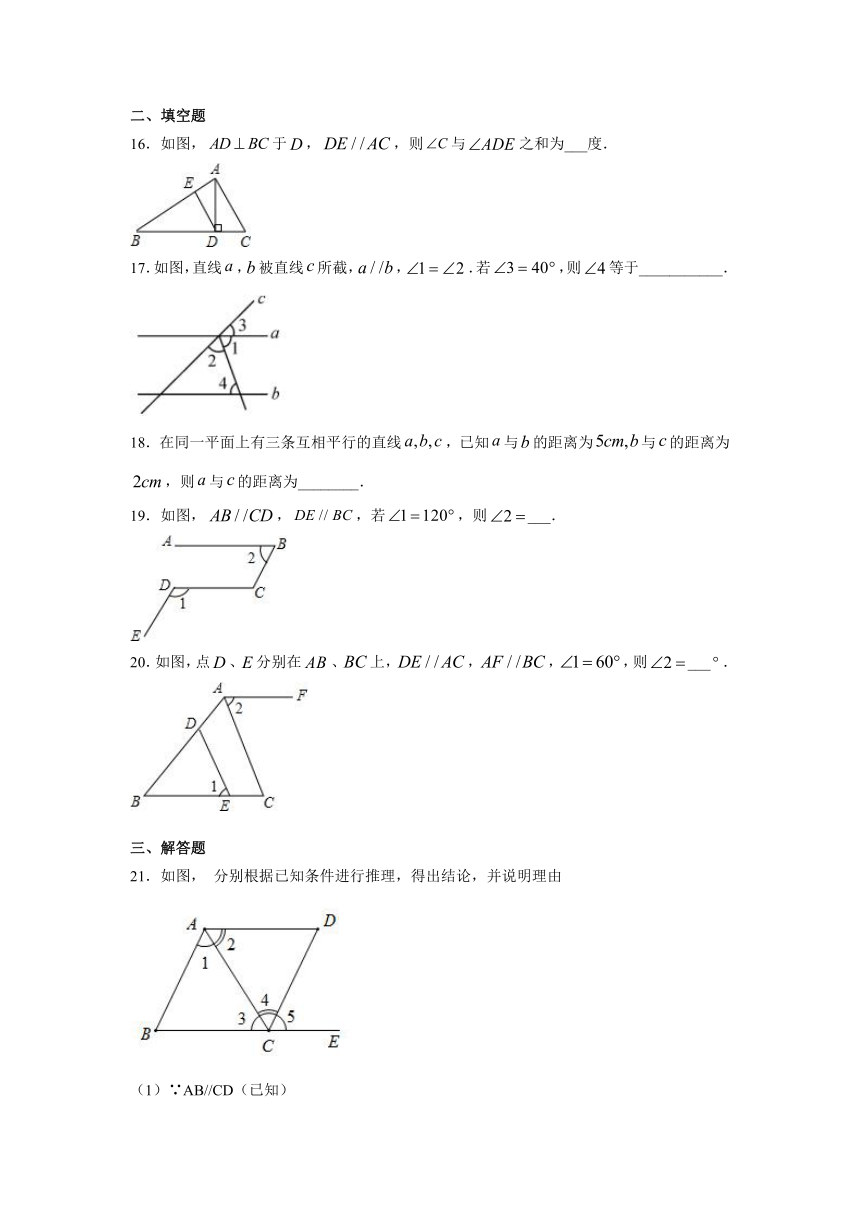
11.如图,已知直线、被直线所截,,若,则等于(
)
A.
B.
C.
D.
12.下列各图形中均有直线,则能使结论成立的是(
)
A.
B.
C.
D.
13.下列命题中,真命题是(
)
A.同位角相等
B.同旁内角相等的两直线平行
C.同旁内角互补
D.平行于同一条直线的两直线平行
14.如图,,将一个含角的直角三角尺按如图所示的方式放置,若的度数为,则的度数为(
)
A.
B.
C.
D.
15.如图,和相交于点,则下列结论正确的是(
)
A.∠1=∠2
B.∠2=∠3
C.∠3=∠4
D.∠1=∠5
二、填空题
16.如图,于,,则与之和为___度.
17.如图,直线,被直线所截,,.若,则等于___________.
18.在同一平面上有三条互相平行的直线,已知与的距离为与的距离为,则与的距离为________.
19.如图,,,若,则___.
20.如图,点、分别在、上,,,,则___.
三、解答题
21.如图,
分别根据已知条件进行推理,得出结论,并说明理由
(1)∵AB//CD(已知)
∴∠
B=∠
(
)
(2)∵AD//BC(已知)
∴∠2=∠
(
)
(3)∵AD//BC(已知)
∴∠BAD+∠
=180°(
)
∵AB//CD(已知)
∴∠BAD+∠
=180°(
)
∴∠B=∠
()
22.如图,,,,求的度数.
(1)请完成下列书写过程.
(已知)
又(已知)
(2)若在平面内取一点,作射线,,则 .
23.如图,在、两处之间要修一条笔直的公路,从地测得公路走向是北偏东,公司要求、两地同时开工,并保证若干天后公路准确接通.
(1)地修公路的走向应该是
;
(2)若公路长12千米,另一条公路长6千米,且的走向是北偏西,试求到公路的距离?
24.如图1,AB∥CD,直线AE分别交AB、CD于点A、E.点F是直线AE上一点,连结BF,BP平分∠ABF,EP平分∠AEC,BP与EP交于点P.
(1)若点F是线段AE上一点,且BF⊥AE,求∠P的度数;
(2)若点F是直线AE上一动点(点F与点A不重合),请直接写出∠P与∠AFB之间的数量关系
参考答案
1--10DBADB
CBCAC
11--15ABDAA
16.90
17.
18.7cm或3cm
19.60°
20.60
21.解:(1)∵AB//CD(已知)
∴∠
B=∠5(两直线平行,同位角相等)
(2)∵AD//BC(已知)
∴∠2=∠3(两直线平行,内错角相等)
(3)∵AD//BC(已知)
∴∠BAD+∠
B
=180°(两直线平行,同旁内角互补)
∵AB//CD(已知)
∴∠BAD+∠
D
=180°(两直线平行,同旁内角互补)
∴∠B=∠
D
.
22.解:(1)(已知),
(两直线平行,同位角相等),
又(已知),
(两直线平行,同位角相等).
故答案为:∠1,两直线平行,同位角相等,∠D,40°,两直线平行,同位角相等;
(2)若在平面内取一点,作射线,,则40°或140°.
故答案为:40°或140°.
23.(1)由两地南北方向平行,根据内错角相等,可知地所修公路的走向是南偏西.
故答案为:南偏西.
(2),
,
地到公路的距离是千米.
24.解:(1)过点P作PQ∥AB,过点F作FH∥AB,
∵AB∥CD,
∴AB∥CD∥PQ∥FH,
∴∠ABP=∠BPQ,∠CEP=∠EPQ,∠ABF=∠BFH,∠CEF=∠EFH,
∴∠ABP+∠CEP=∠BPQ+∠EPQ=∠BPE,∠ABF+∠CEF=∠BFH+∠EFH=∠BFE,
∵BF⊥AE,
∴∠ABF+∠CEF=∠BFE=90°,
∵BP平分∠ABF,EP平分∠AEC,
∴∠ABP+∠CEP=(∠ABF+∠CEF)=45°,
∴∠BPE=45°;
(2)①当点F在EA的延长线上时,∠BPE=∠AFB,理由如下:
如备用图1,
过点P作PQ∥AB,过点F作FH∥AB,
∵AB∥CD,
∴AB∥CD∥PQ∥FH,
∴∠ABP=∠BPQ,∠CEP=∠EPQ,∠ABF=∠BFH,∠CEF=∠EFH,
∴∠CEP﹣∠ABP=∠EPQ﹣∠BPQ=∠BPE,∠CEF﹣∠ABF=∠EFH﹣∠BFH=∠BFE,
∵BP平分∠ABF,EP平分∠AEC,
∴∠CEP﹣∠ABP=(∠CEF﹣∠ABF)=∠BFE=∠AFB,
∴∠BPE=∠AFB;
②当点F在线段AE上(不与A点重合)时,∠BPE=90°﹣∠AFB;理由如下:
如备用图2,
过点P作PQ∥AB,过点F作FH∥AB,
∵AB∥CD,
∴AB∥CD∥PQ∥FH,
∴∠ABP=∠BPQ,∠CEP=∠EPQ,∠ABF=∠BFH,∠CEF=∠EFH,
∴∠ABP+∠CEP=∠BPQ+∠EPQ=∠BPE,∠ABF+∠CEF=∠BFH+∠EFH=∠BFE,
∵BP平分∠ABF,EP平分∠AEC,
∴∠ABP+∠CEP=(∠ABF+∠CEF),
∴∠BPE=∠BFE
∴∠BFE=180°﹣∠AFB,
∴∠BPE=90°﹣∠AFB;
③当点F在AE的延长线上时,∠BPE=90°﹣∠AFB,理由如下:如备用图3,
过点P作PQ∥AB,过点F作FH∥AB,
∵AB∥CD,
∴AB∥CD∥PQ∥FH,
∴∠ABP=∠BPQ,∠CEP=∠EPQ,180°﹣∠ABF=∠BFH,∠AEC=∠EFH,
∴∠CEP+∠ABP=∠EPQ+∠BPQ=∠BPE,∠BFH﹣∠EFH=180°﹣∠ABF﹣∠AEC=∠AFB,
∵BP平分∠ABF,EP平分∠AEC,
∴∠CEP+∠ABP=(∠AEC+∠ABF)=(180°﹣∠AFB),
∴∠BPE=90°﹣∠AFB;
综上,当E点在A点上方时,∠BPE=∠AFB,当E点在A点下方时,∠BPE=90°﹣∠AFB.
一、单选题
1.把命题“同角的余角相等”改写成“如果……那么……”的形式,正确的是(
)
A.如果是同角,那么余角相等
B.如果两个角相等,那么这两个角是同一个角的余角
C.如果是同角的余角,那么相等
D.如果两个角是同一个角的余角,那么这两个角相等
2.如图,已知直线被直线l所截,,若,则的度数是(
)
A.
B.
C.
D.
3.一把直尺和一个含,角的三角板如图所示摆放,直尺一边与三角板的两直角边分别交于,两点,另一边与三角板的两直角边分别交于,两点,且,那么的大小为(
)
A.
B.
C.
D.
4.下列命题与它的逆命题均为真命题的是()
A.内错角相等
B.对顶角相等
C.如果ab0,那么a0
D.互为相反数的两个数和为0
5.下列命题是定理的是(
)
A.内错角相等
B.同位角相等,两直线平行
C.一个角的余角不等于它本身
D.在同一平面内,有且只有一条直线与已知直线垂直
6.下列语句中,不是命题的是( )
A.如果a+b=0,那么a、b互为相反数
B.内错角相等
C.已知a2=4,a的值是多少?
D.负数大于正数
7.如图,已知直线a
//
b
//
c,直线d与它们分别垂直且相交于A,B,C三点,若AB=2,AC=6,则平行线b、c之间的距离是(
)
A.2
B.4
C.6
D.8
8.如图所示,下列推理及括号中所注明的推理依据错误的是(
)
A.,(内错角相等,两直线平行)
B.,(两直线平行,同旁内角互补)
C.,(两直线平行,同旁内角互补)
D.,(同位角相等,两直线平行)
9.如图,已知平分,则的度数是(
)
A.
B.
C.
D.
10.光线在不同介质中的传播速度不同,因此当光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,当∠1=45°,∠2=122°时,∠3和∠4的度数分别是(
)
A.58°,122°
B.45°,68°
C.45°,58°
D.45°,45°
11.如图,已知直线、被直线所截,,若,则等于(
)
A.
B.
C.
D.
12.下列各图形中均有直线,则能使结论成立的是(
)
A.
B.
C.
D.
13.下列命题中,真命题是(
)
A.同位角相等
B.同旁内角相等的两直线平行
C.同旁内角互补
D.平行于同一条直线的两直线平行
14.如图,,将一个含角的直角三角尺按如图所示的方式放置,若的度数为,则的度数为(
)
A.
B.
C.
D.
15.如图,和相交于点,则下列结论正确的是(
)
A.∠1=∠2
B.∠2=∠3
C.∠3=∠4
D.∠1=∠5
二、填空题
16.如图,于,,则与之和为___度.
17.如图,直线,被直线所截,,.若,则等于___________.
18.在同一平面上有三条互相平行的直线,已知与的距离为与的距离为,则与的距离为________.
19.如图,,,若,则___.
20.如图,点、分别在、上,,,,则___.
三、解答题
21.如图,
分别根据已知条件进行推理,得出结论,并说明理由
(1)∵AB//CD(已知)
∴∠
B=∠
(
)
(2)∵AD//BC(已知)
∴∠2=∠
(
)
(3)∵AD//BC(已知)
∴∠BAD+∠
=180°(
)
∵AB//CD(已知)
∴∠BAD+∠
=180°(
)
∴∠B=∠
()
22.如图,,,,求的度数.
(1)请完成下列书写过程.
(已知)
又(已知)
(2)若在平面内取一点,作射线,,则 .
23.如图,在、两处之间要修一条笔直的公路,从地测得公路走向是北偏东,公司要求、两地同时开工,并保证若干天后公路准确接通.
(1)地修公路的走向应该是
;
(2)若公路长12千米,另一条公路长6千米,且的走向是北偏西,试求到公路的距离?
24.如图1,AB∥CD,直线AE分别交AB、CD于点A、E.点F是直线AE上一点,连结BF,BP平分∠ABF,EP平分∠AEC,BP与EP交于点P.
(1)若点F是线段AE上一点,且BF⊥AE,求∠P的度数;
(2)若点F是直线AE上一动点(点F与点A不重合),请直接写出∠P与∠AFB之间的数量关系
参考答案
1--10DBADB
CBCAC
11--15ABDAA
16.90
17.
18.7cm或3cm
19.60°
20.60
21.解:(1)∵AB//CD(已知)
∴∠
B=∠5(两直线平行,同位角相等)
(2)∵AD//BC(已知)
∴∠2=∠3(两直线平行,内错角相等)
(3)∵AD//BC(已知)
∴∠BAD+∠
B
=180°(两直线平行,同旁内角互补)
∵AB//CD(已知)
∴∠BAD+∠
D
=180°(两直线平行,同旁内角互补)
∴∠B=∠
D
.
22.解:(1)(已知),
(两直线平行,同位角相等),
又(已知),
(两直线平行,同位角相等).
故答案为:∠1,两直线平行,同位角相等,∠D,40°,两直线平行,同位角相等;
(2)若在平面内取一点,作射线,,则40°或140°.
故答案为:40°或140°.
23.(1)由两地南北方向平行,根据内错角相等,可知地所修公路的走向是南偏西.
故答案为:南偏西.
(2),
,
地到公路的距离是千米.
24.解:(1)过点P作PQ∥AB,过点F作FH∥AB,
∵AB∥CD,
∴AB∥CD∥PQ∥FH,
∴∠ABP=∠BPQ,∠CEP=∠EPQ,∠ABF=∠BFH,∠CEF=∠EFH,
∴∠ABP+∠CEP=∠BPQ+∠EPQ=∠BPE,∠ABF+∠CEF=∠BFH+∠EFH=∠BFE,
∵BF⊥AE,
∴∠ABF+∠CEF=∠BFE=90°,
∵BP平分∠ABF,EP平分∠AEC,
∴∠ABP+∠CEP=(∠ABF+∠CEF)=45°,
∴∠BPE=45°;
(2)①当点F在EA的延长线上时,∠BPE=∠AFB,理由如下:
如备用图1,
过点P作PQ∥AB,过点F作FH∥AB,
∵AB∥CD,
∴AB∥CD∥PQ∥FH,
∴∠ABP=∠BPQ,∠CEP=∠EPQ,∠ABF=∠BFH,∠CEF=∠EFH,
∴∠CEP﹣∠ABP=∠EPQ﹣∠BPQ=∠BPE,∠CEF﹣∠ABF=∠EFH﹣∠BFH=∠BFE,
∵BP平分∠ABF,EP平分∠AEC,
∴∠CEP﹣∠ABP=(∠CEF﹣∠ABF)=∠BFE=∠AFB,
∴∠BPE=∠AFB;
②当点F在线段AE上(不与A点重合)时,∠BPE=90°﹣∠AFB;理由如下:
如备用图2,
过点P作PQ∥AB,过点F作FH∥AB,
∵AB∥CD,
∴AB∥CD∥PQ∥FH,
∴∠ABP=∠BPQ,∠CEP=∠EPQ,∠ABF=∠BFH,∠CEF=∠EFH,
∴∠ABP+∠CEP=∠BPQ+∠EPQ=∠BPE,∠ABF+∠CEF=∠BFH+∠EFH=∠BFE,
∵BP平分∠ABF,EP平分∠AEC,
∴∠ABP+∠CEP=(∠ABF+∠CEF),
∴∠BPE=∠BFE
∴∠BFE=180°﹣∠AFB,
∴∠BPE=90°﹣∠AFB;
③当点F在AE的延长线上时,∠BPE=90°﹣∠AFB,理由如下:如备用图3,
过点P作PQ∥AB,过点F作FH∥AB,
∵AB∥CD,
∴AB∥CD∥PQ∥FH,
∴∠ABP=∠BPQ,∠CEP=∠EPQ,180°﹣∠ABF=∠BFH,∠AEC=∠EFH,
∴∠CEP+∠ABP=∠EPQ+∠BPQ=∠BPE,∠BFH﹣∠EFH=180°﹣∠ABF﹣∠AEC=∠AFB,
∵BP平分∠ABF,EP平分∠AEC,
∴∠CEP+∠ABP=(∠AEC+∠ABF)=(180°﹣∠AFB),
∴∠BPE=90°﹣∠AFB;
综上,当E点在A点上方时,∠BPE=∠AFB,当E点在A点下方时,∠BPE=90°﹣∠AFB.
