2020-2021学年度广东省河源市5月月考高二数学试卷(Word含解析)
文档属性
| 名称 | 2020-2021学年度广东省河源市5月月考高二数学试卷(Word含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 805.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 00:00:00 | ||
图片预览




文档简介
2020-2021学年度5月月考卷
高二数学试题
(考试范围:新高考数学全部内容;考试时间:120分钟)
第I卷(选择题)
一、单选题(共8个小题,每小题5分,共40分)
1.已知集合,,若,则实数的取值范围是(
)
A.
B.
C.
D.
2.已知等差数列的前项和为,则(
)
A.21
B.11
C.
D.0
3.在假期里,有5名同学去社区做防疫志愿者,根据需要,要安排这5名同学去甲、乙两个核酸检测点,每个检测点至少去2名同学,则不同的安排方法共有(
)
A.10种
B.20种
C.24种
D.30种
4.已知,则(
)
A.
B.
C.
D.
5.已知空间中不过同一点的两条直线,及平面,则“,与平面所成的角相同”是“”的(
).
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
6.若双曲线与直线无交点,则双曲线的离心率的取值范围是(
)
A.
B.
C.
D.
7.已知函数(
)
A.是奇函数,单调递增
B.是奇函数,单调递减
C.是偶函数,单调递减
D.是偶函数,单调递增
8.已知奇函数对任意的都满足,且在上单调递增,若,,,则下列结论正确的是(
)
A.
B.
C.
D.
二、多选题(共4个小题,全对得5分,部分对得2分,共20分)
9.下列命题正确的(
)
A.若复数,则
B.若,,则复数的虚部是
C.若,则的最小值为1
D.已知,若关于x的方程有实数根,则实根必为.
10.已知向量,满足,,,则下列结论中正确的是(
)
A.
B.
C.
D.与的夹角为
11.已知函数,则有(
)
A.
B.
C.是函数图象的对称中心
D.方程有三个实根
12.已知椭圆:,过其左焦点且斜率为的直线在轴上的截距的绝对值大于椭圆的短半轴的长,则以下结论正确的是(
)
A.椭圆的焦距为
B.直线的方程为
C.的取值范围是
D.椭圆C的离心率可以为
第II卷(非选择题)
三、填空题(共4个小题,每小题5分,共20分)
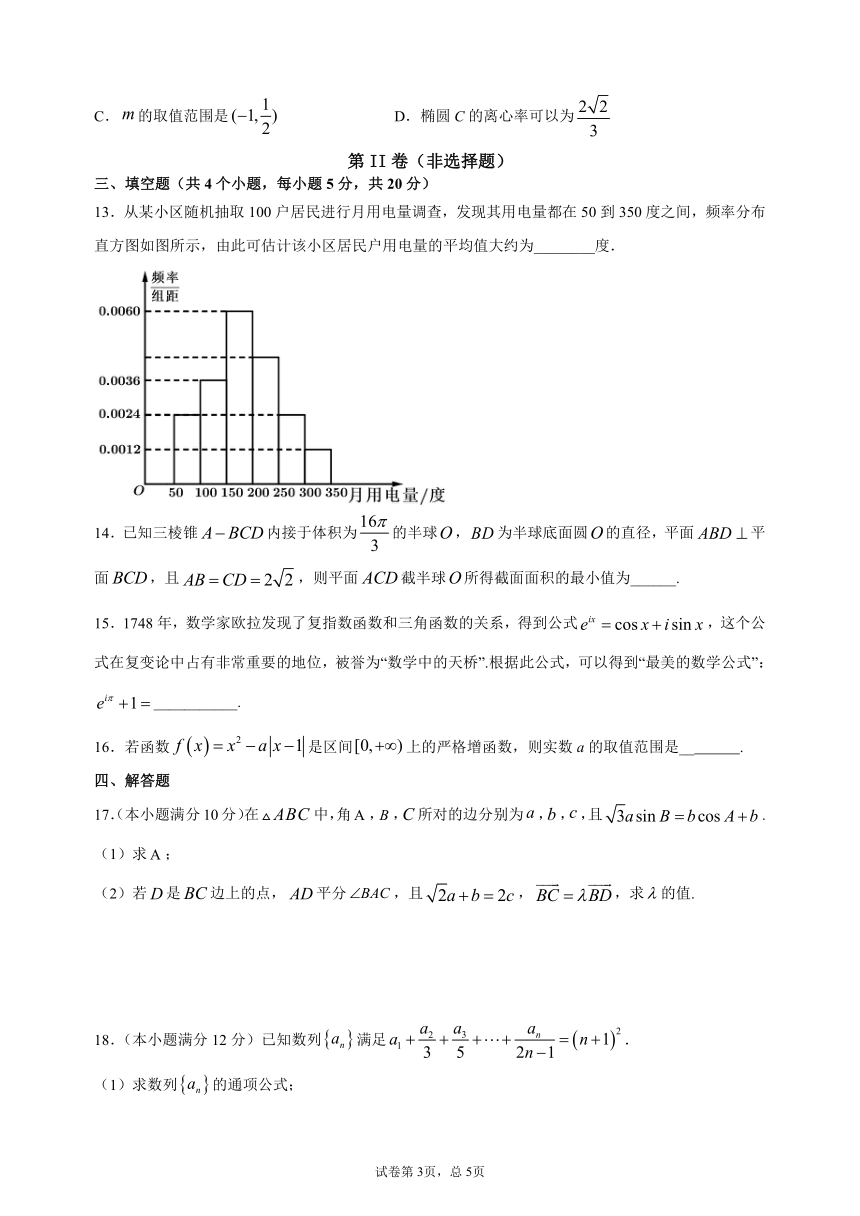
13.从某小区随机抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示,由此可估计该小区居民户用电量的平均值大约为________度.
14.已知三棱锥内接于体积为的半球,为半球底面圆的直径,平面平面,且,则平面截半球所得截面面积的最小值为______.
15.1748年,数学家欧拉发现了复指数函数和三角函数的关系,得到公式,这个公式在复变论中占有非常重要的地位,被誉为“数学中的天桥”.根据此公式,可以得到“最美的数学公式”:___________.
16.若函数是区间上的严格增函数,则实数a的取值范围是__
.
四、解答题
17.(本小题满分10分)在中,角,,所对的边分别为,,,且.
(1)求;
(2)若是边上的点,平分,且,,求的值.
18.(本小题满分12分)已知数列满足.
(1)求数列的通项公式;
(2)若,求数列的前项和.
19.(本小题满分12分)2021年是中国共产党成立100周年,为庆祝中国共产党的百年华诞,某单位举行了关于党史知识的书面测试和演讲比赛两阶段团体比赛,最终由16名职工组成的初心队夺得第一名,他们在书面测试与演讲比赛中的个人成绩(单位:分,满分100分)统计如下:
职工序号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
书面测试成绩
99
99
98
98
97
95
95
95
93
93
92
92
89
89
88
88
演讲比赛成绩
95
92
86
88
91
88
86
91
90
86
85
83
80
80
79
82
(1)设书面测试成绩不低于90分为“书面测试优秀”,书面测试成绩低于90分为“书面测试一般”,演讲比赛成绩不低于85分为“演讲比赛优秀”,演讲比赛成绩低于85分为“演讲比赛一般”,据此完成以下2×2列联表,并判断能否有99.9%的把握认为书面测试成绩与演讲比赛成绩有关?
书面测试优秀
书面测试一般
总计
演讲比赛优秀
演讲比赛一般
总计
(2)从书面测试成绩不低于96分的职工中随机选出2名,记选出的2名职工中演讲比赛成绩不低于90分的人数为,求的分布列及数学期望.
附:,其中.
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
20.(本小题满分12分)已知圆柱底面半径为1,高为,是圆柱的一个轴截面,动点从点出发沿着圆柱的侧面到达点,其距离最短时在侧面留下的曲线如图所示.将轴截面绕着轴逆时针旋转后,边与曲线相交于点.
(1)求曲线的长度;
(2)当时,求点到平面的距离.
21.(本小题满分12分)设双曲线的上焦点为是双曲线上的两个不同的点.
(1)求双曲线的渐近线方程;
(2)若,求点纵坐标的值;
(3)设直线与轴交于点关于轴的对称点为.若三点共线,求证:为定值.
22.(本小题满分12分)已知函数,.
(1)求函数的最小值;
(2)若关于的不等式在恒成立,求实数的取值范围.
试卷第4页,总5页
试卷第5页,总5页
参考答案
1.A【详解】
由题知,又,则,解得,故选:A
2.D【详解】由,得,所以,则,所以.故选:D.
3.B【详解】根据题意,分2步进行分析:
①将5人分为2组,每组至少2人,所以只能分为2和3的两组,有种方法;
②将分好的2组全排列,安排到2个社区,有种情况,
则共有种不同的安排方法.故选:B.
4.D【详解】令,可得,,所以.故选:D.
5.B【详解】
如图,
当,与平面所成的角相同,,而此时不共平行,故不成立,
反之,则,与平面所成的角相同成立,故选:B.
6.A【详解】双曲线的渐近线为,双曲线与直线没有公共点,
则,则,,.故选:A.
7.D【详解】定义域为,因为,所以为偶函数,任取,且,则
,因为,,所以,所以,所以在单调递增,
故选:D
8.B【详解】令,则,因为都是奇函数,所以是偶函数,因为,所以,,
即,所以的周期为,
因为都在上单调递增,
所以且它们不恒为零
,
则在上成立(不恒为零),
所以在上单调递增,且,
又,且,
所以,故选:B
9.AC【详解】
对A选项,,故,A正确;
对B选项,,故虚部为2,B错误;
对C选项,设,且,
则,所以
因为,当时最小值为1,故C正确;
对D选项,关于x的方程有实数根,
则
解得,故D错误.
故选:AC
10.BC【详解】,∴,
∴,∴,,
,∴与的夹角为,故BC正确.故选:BC.
11.ABC【详解】
因为函数,
A.
因为,故正确;
B.
因为,所以,故正确;
C.
因为,所以是函数图象的对称中心,故正确;
D.在同一坐标系中作出函数的图象:
由图象可知:方程的实根超过3个,故错误;
故选:ABC
12.BCD【详解】由题意可知:,左焦点为,所以椭圆的焦距为,故选项A错误;直线的方程为:,选项B正确;
当时,,又直线在轴上的截距的绝对值大于椭圆的短半轴的长,所以,即,所以,所以,又,所以,即,所以选项C,D正确.故选:BCD.
13.186【详解】
设用电量在200到250度之间之间的频数为,
则有,
由频率分布直方图可知:
由题意可知:估计该小区居民户用电量的平均值大约为:
故答案为:
14.
【详解】由半球的体积为可得半球的半径为2,如图1,连接,,则,因为,所以,,即,,又平面平面,平面平面,所以,则,所以外接圆的半径为,
结合图1可知当或位于底面圆上时,平面截面球所得截面面积最小,
不妨令在底面圆上,则底面圆与外接圆的交线为,
所得截面如图2所示,易知对应的圆心角为,
则所得截面面积,所以所求截面面积的最小值为.故答案为:.
15.0【详解】,.
16.【详解】
,要使函数在单调递增,则在单调递增,且在单调递增,以及在分界点处,即得
,解得:.
故答案为:
17.(1);(2).
解:
(1)由正弦定理可得,因为,
所以,则,因为,所以,
所以,得.
(2)由,得,①
由余弦定理可得,②
联立①②得,则,所以,
依题意得,因为,所以
18.(1);(2).
解:(1)∵,①
∴当时,,②
①-②得,则.
当时,由①得,不满足上式,
∴
(2)由(1)知,,
∴当时,.
当时,,满足上式,故.
19.
【详解】
(1)完成的2×2列联表如下:
书面测试优秀
书面测试一般
总计
演讲比赛优秀
11
0
11
演讲比赛一般
1
4
5
总计
12
4
16
由表格可得,
由于11.733>10.828,故有99.9%的把握认为书面测试成绩与演讲比赛成绩有关.
(2)根据题意可知,书面测试成绩不低于96分的有5人,
其中演讲比赛成绩不低于90分的有3人,
故的所有可能取值为0,1,2,
且,,
故的分布列为
0
1
2
数学期望.
20.(1);(2)
【详解】
(1)曲线的长度为矩形的对角线长度.其中矩形的宽为圆柱的高,长为底面的半圆长,
其中,底面的半圆长为
∴的长为
(2)当时,建立如图所示的空间直角坐标系:
则有、、、,
所以、、.
设平面的法向量为,
则,代入可得,令,得,
所以点到平面的距离为.
【点睛】
本题考查了圆柱的展开图及距离的求法,利用空间向量求点到平面距离,属于中档题.
21.【详解】
(1)令则,
∴双曲线的渐近线方程为.
(2)由题意知,,
设为,则,且,
又,解得,
所以点M纵坐标的值为
(3)①当直线MN的斜率不存在时,其方程为与轴有无数个交点,不符合题意;
②当直线的斜率存在时,设为,则其方程为,
设,则,
联立,得,
所以,
因为三点共线,
所以,即,即,
所以,即,
所以,化简得,为定值,
22.解:(1),.
令,则
因为在上恒成立,所以在上单调递增.
又因为,所以当时,;当时,.
即,当时,;当时,,
所以在上单调递减,在上单调递增,
因此,的最小值为;
(2)不等式等价于.
设,则由题意得在内恒成立,
,.
①当时,,这时,使当时,,
从而在上单调递减,又因为,所以当时,
,这与在内恒成立不符.
②当时,对于任意的,,从而,这时.
设,则
设,则,
当时,,所以在上单调递增,
又因为,所以当时,,即,
因此,,所以在上单调递增,
又因为,所以当时,,从而.
综上,实数的取值范围为.
10
3
高二数学试题
(考试范围:新高考数学全部内容;考试时间:120分钟)
第I卷(选择题)
一、单选题(共8个小题,每小题5分,共40分)
1.已知集合,,若,则实数的取值范围是(
)
A.
B.
C.
D.
2.已知等差数列的前项和为,则(
)
A.21
B.11
C.
D.0
3.在假期里,有5名同学去社区做防疫志愿者,根据需要,要安排这5名同学去甲、乙两个核酸检测点,每个检测点至少去2名同学,则不同的安排方法共有(
)
A.10种
B.20种
C.24种
D.30种
4.已知,则(
)
A.
B.
C.
D.
5.已知空间中不过同一点的两条直线,及平面,则“,与平面所成的角相同”是“”的(
).
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
6.若双曲线与直线无交点,则双曲线的离心率的取值范围是(
)
A.
B.
C.
D.
7.已知函数(
)
A.是奇函数,单调递增
B.是奇函数,单调递减
C.是偶函数,单调递减
D.是偶函数,单调递增
8.已知奇函数对任意的都满足,且在上单调递增,若,,,则下列结论正确的是(
)
A.
B.
C.
D.
二、多选题(共4个小题,全对得5分,部分对得2分,共20分)
9.下列命题正确的(
)
A.若复数,则
B.若,,则复数的虚部是
C.若,则的最小值为1
D.已知,若关于x的方程有实数根,则实根必为.
10.已知向量,满足,,,则下列结论中正确的是(
)
A.
B.
C.
D.与的夹角为
11.已知函数,则有(
)
A.
B.
C.是函数图象的对称中心
D.方程有三个实根
12.已知椭圆:,过其左焦点且斜率为的直线在轴上的截距的绝对值大于椭圆的短半轴的长,则以下结论正确的是(
)
A.椭圆的焦距为
B.直线的方程为
C.的取值范围是
D.椭圆C的离心率可以为
第II卷(非选择题)
三、填空题(共4个小题,每小题5分,共20分)
13.从某小区随机抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示,由此可估计该小区居民户用电量的平均值大约为________度.
14.已知三棱锥内接于体积为的半球,为半球底面圆的直径,平面平面,且,则平面截半球所得截面面积的最小值为______.
15.1748年,数学家欧拉发现了复指数函数和三角函数的关系,得到公式,这个公式在复变论中占有非常重要的地位,被誉为“数学中的天桥”.根据此公式,可以得到“最美的数学公式”:___________.
16.若函数是区间上的严格增函数,则实数a的取值范围是__
.
四、解答题
17.(本小题满分10分)在中,角,,所对的边分别为,,,且.
(1)求;
(2)若是边上的点,平分,且,,求的值.
18.(本小题满分12分)已知数列满足.
(1)求数列的通项公式;
(2)若,求数列的前项和.
19.(本小题满分12分)2021年是中国共产党成立100周年,为庆祝中国共产党的百年华诞,某单位举行了关于党史知识的书面测试和演讲比赛两阶段团体比赛,最终由16名职工组成的初心队夺得第一名,他们在书面测试与演讲比赛中的个人成绩(单位:分,满分100分)统计如下:
职工序号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
书面测试成绩
99
99
98
98
97
95
95
95
93
93
92
92
89
89
88
88
演讲比赛成绩
95
92
86
88
91
88
86
91
90
86
85
83
80
80
79
82
(1)设书面测试成绩不低于90分为“书面测试优秀”,书面测试成绩低于90分为“书面测试一般”,演讲比赛成绩不低于85分为“演讲比赛优秀”,演讲比赛成绩低于85分为“演讲比赛一般”,据此完成以下2×2列联表,并判断能否有99.9%的把握认为书面测试成绩与演讲比赛成绩有关?
书面测试优秀
书面测试一般
总计
演讲比赛优秀
演讲比赛一般
总计
(2)从书面测试成绩不低于96分的职工中随机选出2名,记选出的2名职工中演讲比赛成绩不低于90分的人数为,求的分布列及数学期望.
附:,其中.
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
20.(本小题满分12分)已知圆柱底面半径为1,高为,是圆柱的一个轴截面,动点从点出发沿着圆柱的侧面到达点,其距离最短时在侧面留下的曲线如图所示.将轴截面绕着轴逆时针旋转后,边与曲线相交于点.
(1)求曲线的长度;
(2)当时,求点到平面的距离.
21.(本小题满分12分)设双曲线的上焦点为是双曲线上的两个不同的点.
(1)求双曲线的渐近线方程;
(2)若,求点纵坐标的值;
(3)设直线与轴交于点关于轴的对称点为.若三点共线,求证:为定值.
22.(本小题满分12分)已知函数,.
(1)求函数的最小值;
(2)若关于的不等式在恒成立,求实数的取值范围.
试卷第4页,总5页
试卷第5页,总5页
参考答案
1.A【详解】
由题知,又,则,解得,故选:A
2.D【详解】由,得,所以,则,所以.故选:D.
3.B【详解】根据题意,分2步进行分析:
①将5人分为2组,每组至少2人,所以只能分为2和3的两组,有种方法;
②将分好的2组全排列,安排到2个社区,有种情况,
则共有种不同的安排方法.故选:B.
4.D【详解】令,可得,,所以.故选:D.
5.B【详解】
如图,
当,与平面所成的角相同,,而此时不共平行,故不成立,
反之,则,与平面所成的角相同成立,故选:B.
6.A【详解】双曲线的渐近线为,双曲线与直线没有公共点,
则,则,,.故选:A.
7.D【详解】定义域为,因为,所以为偶函数,任取,且,则
,因为,,所以,所以,所以在单调递增,
故选:D
8.B【详解】令,则,因为都是奇函数,所以是偶函数,因为,所以,,
即,所以的周期为,
因为都在上单调递增,
所以且它们不恒为零
,
则在上成立(不恒为零),
所以在上单调递增,且,
又,且,
所以,故选:B
9.AC【详解】
对A选项,,故,A正确;
对B选项,,故虚部为2,B错误;
对C选项,设,且,
则,所以
因为,当时最小值为1,故C正确;
对D选项,关于x的方程有实数根,
则
解得,故D错误.
故选:AC
10.BC【详解】,∴,
∴,∴,,
,∴与的夹角为,故BC正确.故选:BC.
11.ABC【详解】
因为函数,
A.
因为,故正确;
B.
因为,所以,故正确;
C.
因为,所以是函数图象的对称中心,故正确;
D.在同一坐标系中作出函数的图象:
由图象可知:方程的实根超过3个,故错误;
故选:ABC
12.BCD【详解】由题意可知:,左焦点为,所以椭圆的焦距为,故选项A错误;直线的方程为:,选项B正确;
当时,,又直线在轴上的截距的绝对值大于椭圆的短半轴的长,所以,即,所以,所以,又,所以,即,所以选项C,D正确.故选:BCD.
13.186【详解】
设用电量在200到250度之间之间的频数为,
则有,
由频率分布直方图可知:
由题意可知:估计该小区居民户用电量的平均值大约为:
故答案为:
14.
【详解】由半球的体积为可得半球的半径为2,如图1,连接,,则,因为,所以,,即,,又平面平面,平面平面,所以,则,所以外接圆的半径为,
结合图1可知当或位于底面圆上时,平面截面球所得截面面积最小,
不妨令在底面圆上,则底面圆与外接圆的交线为,
所得截面如图2所示,易知对应的圆心角为,
则所得截面面积,所以所求截面面积的最小值为.故答案为:.
15.0【详解】,.
16.【详解】
,要使函数在单调递增,则在单调递增,且在单调递增,以及在分界点处,即得
,解得:.
故答案为:
17.(1);(2).
解:
(1)由正弦定理可得,因为,
所以,则,因为,所以,
所以,得.
(2)由,得,①
由余弦定理可得,②
联立①②得,则,所以,
依题意得,因为,所以
18.(1);(2).
解:(1)∵,①
∴当时,,②
①-②得,则.
当时,由①得,不满足上式,
∴
(2)由(1)知,,
∴当时,.
当时,,满足上式,故.
19.
【详解】
(1)完成的2×2列联表如下:
书面测试优秀
书面测试一般
总计
演讲比赛优秀
11
0
11
演讲比赛一般
1
4
5
总计
12
4
16
由表格可得,
由于11.733>10.828,故有99.9%的把握认为书面测试成绩与演讲比赛成绩有关.
(2)根据题意可知,书面测试成绩不低于96分的有5人,
其中演讲比赛成绩不低于90分的有3人,
故的所有可能取值为0,1,2,
且,,
故的分布列为
0
1
2
数学期望.
20.(1);(2)
【详解】
(1)曲线的长度为矩形的对角线长度.其中矩形的宽为圆柱的高,长为底面的半圆长,
其中,底面的半圆长为
∴的长为
(2)当时,建立如图所示的空间直角坐标系:
则有、、、,
所以、、.
设平面的法向量为,
则,代入可得,令,得,
所以点到平面的距离为.
【点睛】
本题考查了圆柱的展开图及距离的求法,利用空间向量求点到平面距离,属于中档题.
21.【详解】
(1)令则,
∴双曲线的渐近线方程为.
(2)由题意知,,
设为,则,且,
又,解得,
所以点M纵坐标的值为
(3)①当直线MN的斜率不存在时,其方程为与轴有无数个交点,不符合题意;
②当直线的斜率存在时,设为,则其方程为,
设,则,
联立,得,
所以,
因为三点共线,
所以,即,即,
所以,即,
所以,化简得,为定值,
22.解:(1),.
令,则
因为在上恒成立,所以在上单调递增.
又因为,所以当时,;当时,.
即,当时,;当时,,
所以在上单调递减,在上单调递增,
因此,的最小值为;
(2)不等式等价于.
设,则由题意得在内恒成立,
,.
①当时,,这时,使当时,,
从而在上单调递减,又因为,所以当时,
,这与在内恒成立不符.
②当时,对于任意的,,从而,这时.
设,则
设,则,
当时,,所以在上单调递增,
又因为,所以当时,,即,
因此,,所以在上单调递增,
又因为,所以当时,,从而.
综上,实数的取值范围为.
10
3
同课章节目录
