9.5 相似三角形判定定理的证明 课件(共34张PPT)
文档属性
| 名称 | 9.5 相似三角形判定定理的证明 课件(共34张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 06:47:03 | ||
图片预览




文档简介
第九章 图形的相似
4 探索三角形相似的条件及
5 相似三角形判定定理的证明
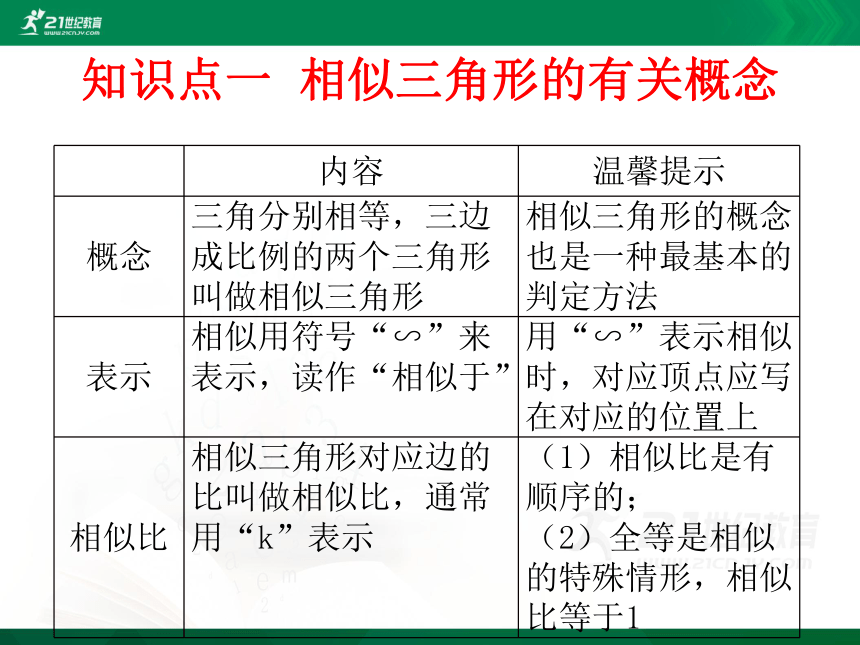
知识点一 相似三角形的有关概念
内容
温馨提示
概念
三角分别相等,三边成比例的两个三角形叫做相似三角形
相似三角形的概念也是一种最基本的判定方法
表示
相似用符号“∽”来表示,读作“相似于”
用“∽”表示相似时,对应顶点应写在对应的位置上
相似比
相似三角形对应边的比叫做相似比,通常用“k”表示
(1)相似比是有顺序的;
(2)全等是相似的特殊情形,相似比等于1
性质
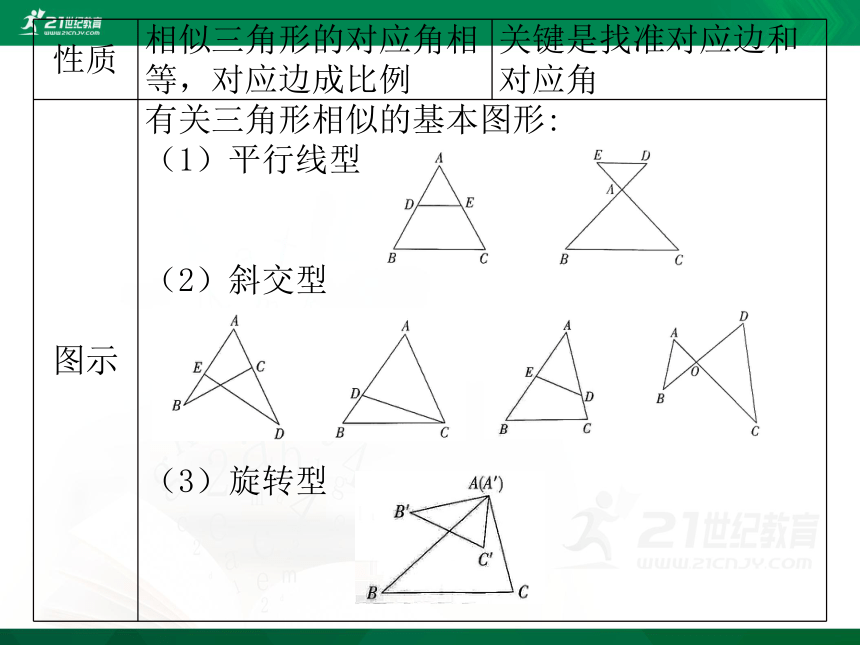
相似三角形的对应角相等,对应边成比例
关键是找准对应边和对应角
图示
有关三角形相似的基本图形:
(1)平行线型
(2)斜交型
(3)旋转型
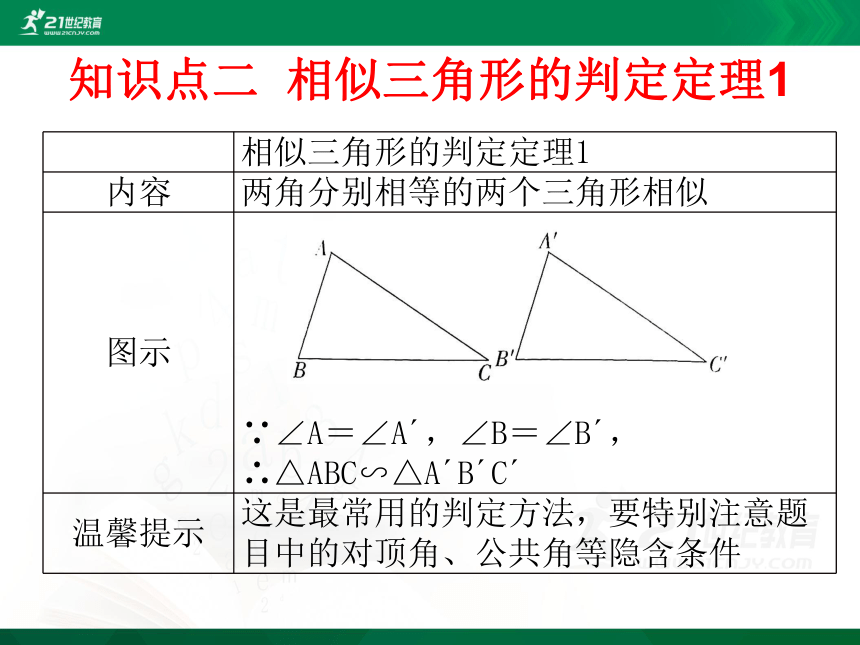
知识点二 相似三角形的判定定理1
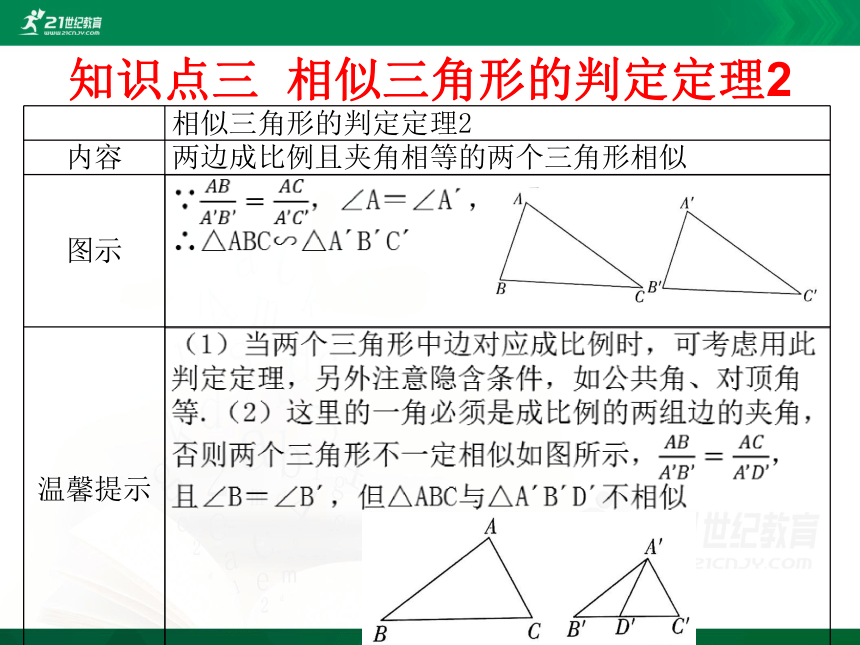
相似三角形的判定定理1
内容
两角分别相等的两个三角形相似
图示
∵∠A=∠A?,∠B=∠B?,∴△ABC∽△A?B?C?
温馨提示
这是最常用的判定方法,要特别注意题目中的对顶角、公共角等隐含条件
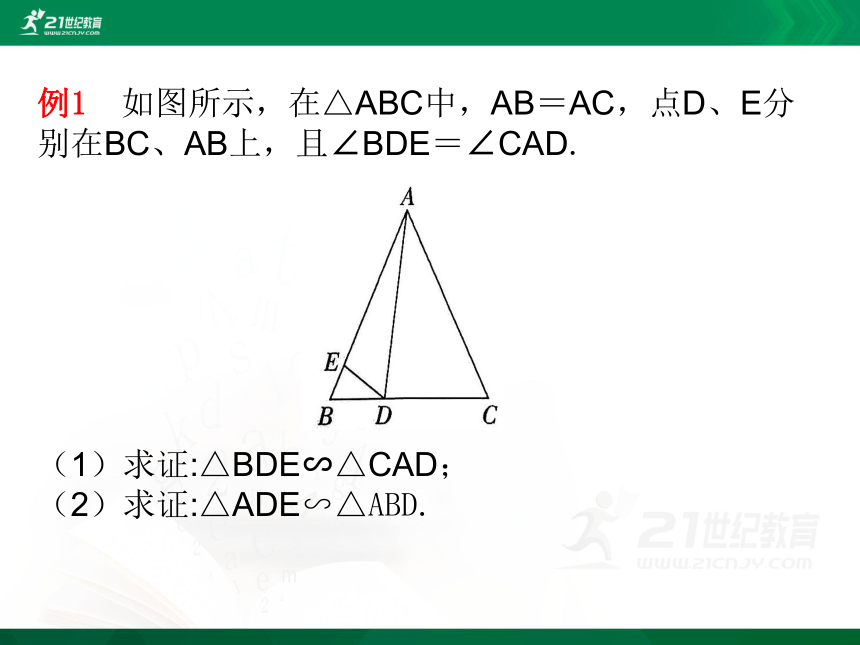
例1 如图所示,在△ABC中,AB=AC,点D、E分别在BC、AB上,且∠BDE=∠CAD.
(1)求证:△BDE∽△CAD;
(2)求证:△ADE∽△ABD.
分析(1)先利用等腰三角形的性质得出∠B=∠C,再由∠BDE=∠CAD可证得△BDE∽△CAD;
(2)先由(1)中相似三角形的性质得∠BED=∠CDA,再利用等角的补角相等,证得∠AED=∠ADB,然后结合两个三角形有一个公共角可证得结论.
分析(1)先利用等腰三角形的性质得出∠B=∠C,再由∠BDE=∠CAD可证得△BDE∽△CAD;
(2)先由(1)中相似三角形的性质得∠BED=∠CDA,再利用等角的补角相等,证得∠AED=∠ADB,然后结合两个三角形有一个公共角可证得结论.
证明 (1)∵AB=AC,∴∠B=∠C,
又∵∠BDE=∠CAD,∴△BDE∽△CAD.
(2)∵△BDE∽△CAD∴∠BED=∠CDA,
∴180°-∠BED=180°-∠CDA,即∠AED=∠ADB,
又∵∠BAD=∠DAE,∴△ADE∽△ABD.
知识点三 相似三角形的判定定理2
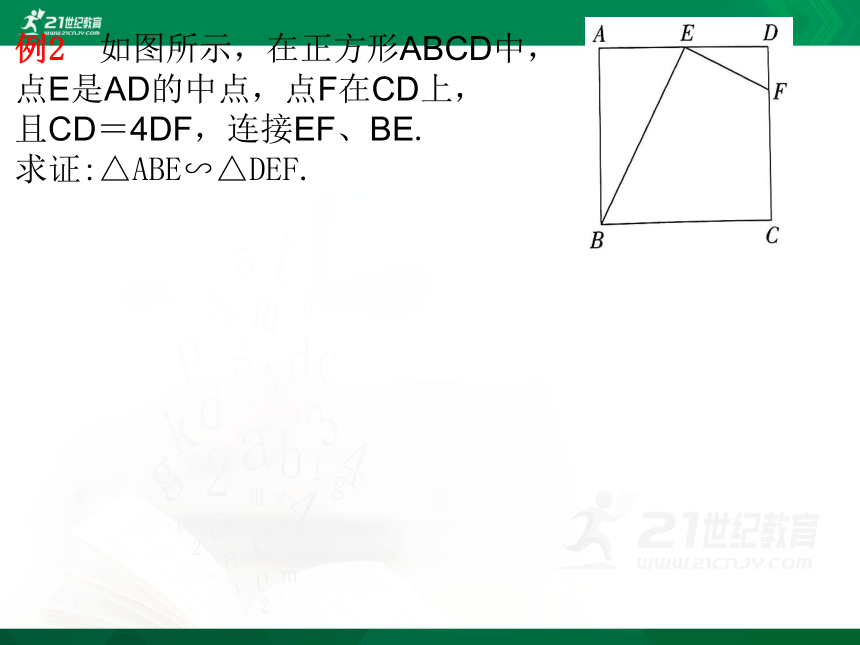
例2 如图所示,在正方形ABCD中,
点E是AD的中点,点F在CD上,
且CD=4DF,连接EF、BE.
求证:△ABE∽△DEF.
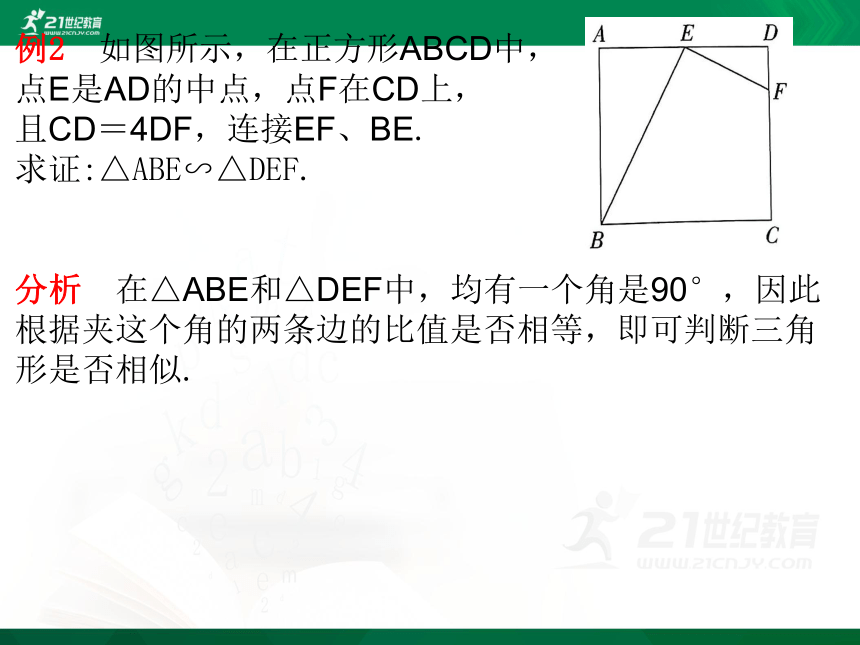
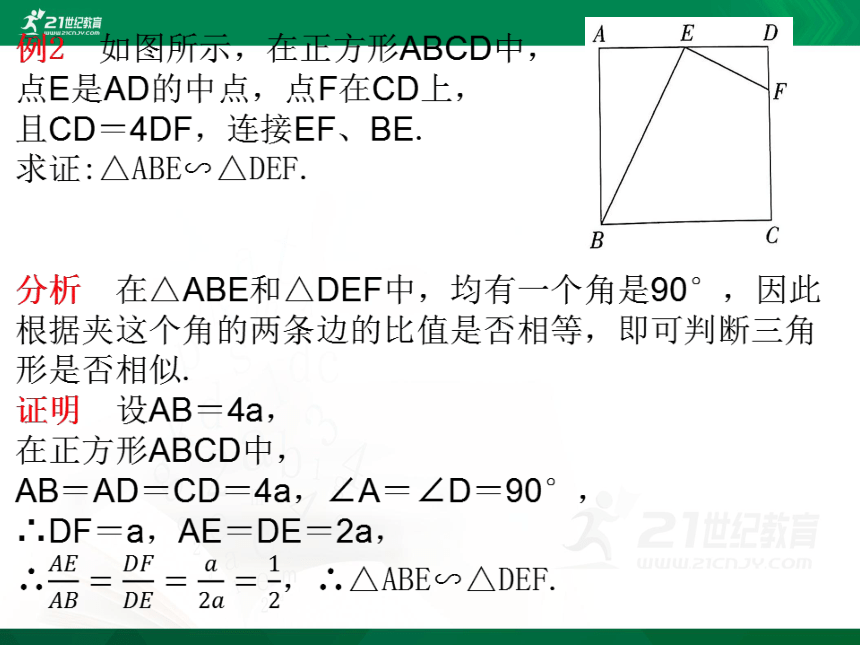
例2 如图所示,在正方形ABCD中,
点E是AD的中点,点F在CD上,
且CD=4DF,连接EF、BE.
求证:△ABE∽△DEF.
分析 在△ABE和△DEF中,均有一个角是90°,因此根据夹这个角的两条边的比值是否相等,即可判断三角形是否相似.
知识点四 相似三角形的判定定理3
例3 如图所示,在△ABC中,点D,E分别是△ABC的边AB,AC上的点,AD=3,AE=6,DE=5,BD=15,CE=3,BC=15.根据以上条件,你认为∠B=∠AED吗?并说明理由.
题型一 添加条件使两个三角形相似
例1 如图所示,点P在△ABC的边AC上,请你添加一个条件,使得△APB∽△ABC,这个条件可以是________.
题型一 添加条件使两个三角形相似
题型一 添加条件使两个三角形相似
题型一 添加条件使两个三角形相似
题型二 网格中的相似三角形的判定
例2 如图所示,在4×3的正方形网格中,△ABC与△CED的顶点都在边长为1的小正方形的顶点上.
(1)填空:∠ABC=_________,BC=_________;
(2)判断△ABC与△CED是否相似,并说明理由.
点拨 本题考查相似三角形的判定,解答本题的关键是根据勾股定理求出网格中相关线段的长,进而利用“两边对应成比例且夹角相等的两个三角形相似”的判定定理证明.
题型三 相似三角形的判定与性质的综合运用
点拨 证等积式往往先把等积式化成比例式,然后通过证明三角形相似来推比例式.
题型四 动态相似图形问题
例4 如图所示,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动如果P,Q分别从A,B同时出发,经过几秒后,△PBQ与△ABC相似?
分析 因为点P,Q在移动过程中,△PBQ与△ABC有公共角,所以只需夹公共角的两边对应成比例,这两个三角形就相似,因为没有明确夹∠B两边的对应关系,所以就存在两种对应关系,所以应分两种情况讨论.
点拨 对于动态相似图形问题,一般是已知命题的结论,求使结论成立的条件,解此类问题可采用逆向思维,把结论视为条件的一部分,再结合已有的条件和图形进行分析、探究,便可得到所需的条件.
易错易混
易错点 误认为两边成比例且有一组角相等的两个三角形相似
易错警示 证明两个三角形相似时,若条件为两边成比例和一组角相等,一定注意看该组角是不是成比例的两边的夹角,不是夹角不能判定两个三角形相似(直角三角形除外).
4 探索三角形相似的条件及
5 相似三角形判定定理的证明
知识点一 相似三角形的有关概念
内容
温馨提示
概念
三角分别相等,三边成比例的两个三角形叫做相似三角形
相似三角形的概念也是一种最基本的判定方法
表示
相似用符号“∽”来表示,读作“相似于”
用“∽”表示相似时,对应顶点应写在对应的位置上
相似比
相似三角形对应边的比叫做相似比,通常用“k”表示
(1)相似比是有顺序的;
(2)全等是相似的特殊情形,相似比等于1
性质
相似三角形的对应角相等,对应边成比例
关键是找准对应边和对应角
图示
有关三角形相似的基本图形:
(1)平行线型
(2)斜交型
(3)旋转型
知识点二 相似三角形的判定定理1
相似三角形的判定定理1
内容
两角分别相等的两个三角形相似
图示
∵∠A=∠A?,∠B=∠B?,∴△ABC∽△A?B?C?
温馨提示
这是最常用的判定方法,要特别注意题目中的对顶角、公共角等隐含条件
例1 如图所示,在△ABC中,AB=AC,点D、E分别在BC、AB上,且∠BDE=∠CAD.
(1)求证:△BDE∽△CAD;
(2)求证:△ADE∽△ABD.
分析(1)先利用等腰三角形的性质得出∠B=∠C,再由∠BDE=∠CAD可证得△BDE∽△CAD;
(2)先由(1)中相似三角形的性质得∠BED=∠CDA,再利用等角的补角相等,证得∠AED=∠ADB,然后结合两个三角形有一个公共角可证得结论.
分析(1)先利用等腰三角形的性质得出∠B=∠C,再由∠BDE=∠CAD可证得△BDE∽△CAD;
(2)先由(1)中相似三角形的性质得∠BED=∠CDA,再利用等角的补角相等,证得∠AED=∠ADB,然后结合两个三角形有一个公共角可证得结论.
证明 (1)∵AB=AC,∴∠B=∠C,
又∵∠BDE=∠CAD,∴△BDE∽△CAD.
(2)∵△BDE∽△CAD∴∠BED=∠CDA,
∴180°-∠BED=180°-∠CDA,即∠AED=∠ADB,
又∵∠BAD=∠DAE,∴△ADE∽△ABD.
知识点三 相似三角形的判定定理2
例2 如图所示,在正方形ABCD中,
点E是AD的中点,点F在CD上,
且CD=4DF,连接EF、BE.
求证:△ABE∽△DEF.
例2 如图所示,在正方形ABCD中,
点E是AD的中点,点F在CD上,
且CD=4DF,连接EF、BE.
求证:△ABE∽△DEF.
分析 在△ABE和△DEF中,均有一个角是90°,因此根据夹这个角的两条边的比值是否相等,即可判断三角形是否相似.
知识点四 相似三角形的判定定理3
例3 如图所示,在△ABC中,点D,E分别是△ABC的边AB,AC上的点,AD=3,AE=6,DE=5,BD=15,CE=3,BC=15.根据以上条件,你认为∠B=∠AED吗?并说明理由.
题型一 添加条件使两个三角形相似
例1 如图所示,点P在△ABC的边AC上,请你添加一个条件,使得△APB∽△ABC,这个条件可以是________.
题型一 添加条件使两个三角形相似
题型一 添加条件使两个三角形相似
题型一 添加条件使两个三角形相似
题型二 网格中的相似三角形的判定
例2 如图所示,在4×3的正方形网格中,△ABC与△CED的顶点都在边长为1的小正方形的顶点上.
(1)填空:∠ABC=_________,BC=_________;
(2)判断△ABC与△CED是否相似,并说明理由.
点拨 本题考查相似三角形的判定,解答本题的关键是根据勾股定理求出网格中相关线段的长,进而利用“两边对应成比例且夹角相等的两个三角形相似”的判定定理证明.
题型三 相似三角形的判定与性质的综合运用
点拨 证等积式往往先把等积式化成比例式,然后通过证明三角形相似来推比例式.
题型四 动态相似图形问题
例4 如图所示,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动如果P,Q分别从A,B同时出发,经过几秒后,△PBQ与△ABC相似?
分析 因为点P,Q在移动过程中,△PBQ与△ABC有公共角,所以只需夹公共角的两边对应成比例,这两个三角形就相似,因为没有明确夹∠B两边的对应关系,所以就存在两种对应关系,所以应分两种情况讨论.
点拨 对于动态相似图形问题,一般是已知命题的结论,求使结论成立的条件,解此类问题可采用逆向思维,把结论视为条件的一部分,再结合已有的条件和图形进行分析、探究,便可得到所需的条件.
易错易混
易错点 误认为两边成比例且有一组角相等的两个三角形相似
易错警示 证明两个三角形相似时,若条件为两边成比例和一组角相等,一定注意看该组角是不是成比例的两边的夹角,不是夹角不能判定两个三角形相似(直角三角形除外).
