人教高中数学必修五2.2等差数列 课件(21张ppt)
文档属性
| 名称 | 人教高中数学必修五2.2等差数列 课件(21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
温故知新
数列有哪些表示方法?
数列与函数的关系?
你还记得吗?
研究发现我国儿童年龄在2-12周岁之间,其标准的身高、体重大致成规律性变化:
你能预测12岁儿童的身高和体重吗?
相差7
年龄
2
3
4
5
6
…
11
12
身高(cm)
84
91
98
105
112
…
147
体重(kg)
12
14
16
18
20
…
30
相差2
154
32
(1)84,91,98,105,112,…,147,154.
(2)12,14,16,18,20,…,30,32
1896年,雅典举行第一届现代奥运会,到2012年的伦敦奥运会已经是第30届奥运会。
(3)1896,1900,1904,…,2008,2012,(
)
你能预测出第31届奥运会的时间吗?
2016
相差4
五
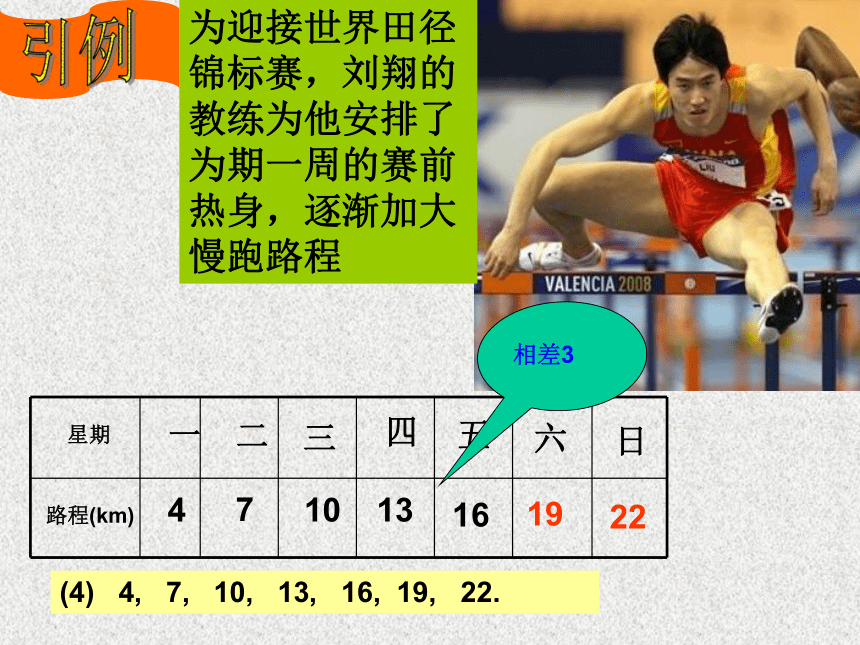
(4)
4,
7,
10,
13,
16,
19,
22.
星期
路程(km)
一
二
三
4
7
10
日
22
四
13
16
六
19
相差3
为迎接世界田径锦标赛,刘翔的教练为他安排了为期一周的赛前热身,逐渐加大慢跑路程
(1)
84,91,98,105,112,…,147,154.
(2)
12,14,16,18,20,…,30,32
(3)
1996,2000,2004,2008,2012,2016
(4)
4,
7,
10,
13,
16,
19,
22.
请问:它们有什么共同特点?
共同特点:从第2项起,每一项与它的前一项的差等于同一个常数。
定义:如果一个数列从第2项起,每一项与它的前一项
的差都等于同一个常数,那么这个数列就叫做等差数列.
这个常数叫做等差数列的公差,公差通常用
d
表示.
d=7
d=2
d=4
d=3
是
不是
不是
判断下列各组数列中哪些是等差数列,哪些不是?如果是,写出首项a1和公差d,
如果不是,说明理由。
(1)1,3,5,7,…
(2)9,6,3,0,-3…
(3)-8,-6,-4,-2,0,…
(4)3,3,3,3,…
(6)15,12,10,8,6,…
小结:判断一个数列是不是等差数列,主要是由定义进行判断:
an+1-an是不是同一个常数?
是
是
是
a1=1,d=2
a1=9,d=-3
a1=-8,d=2
a1=3,d=0
在如下的两个数之间,插入一个什么数后这三个数就会成为一个等差数列:
(1)2
,(
)
,
4
(2)-12,(
)
,0
3
-6
如果在a与b中间插入一个数A,使a,A,b成等差数列,那么A叫做a与b的等差中项。
(
3
)
,
(
)
,
通项公式:
如果一个数列
是等差数列,它的公差是d,那么
…,
…
例1
(1)
求等差数列8,5,2,…,的第20项。
解:
(2)-401是不是等差数列-5,-9,-13…的项?如果是,是第几项?
解:
因此,
解得
,
20
,
3
8
5
,
8
1
=
-
=
-
=
=
n
d
a
Q
用一下
在等差数列中,已知a5=10,a12=31,
解:由题意可知
即这个等差数列的首项是-2,公差是3.
求首项a1与公差d.
解得:
说明:由此可以看到:已知等差数列的两项就
可以确定这个数列.
练一练
练一练
在等差数列中
例2、已知数列的通项公式为
,其中p,q是常数,那么这种数列是否一定是等差数列?如果是,其首项与公差是什么?
探究:在坐标系中画出下列数列的图像
(1)数列:-2,0,2,4,6,8,10,…
(2)数列:7,4,1,-2,…
(3)数列:4,4,4,4,4,4,4,…
等差数列的图象1
(1)数列:-2,0,2,4,6,8,10,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
●
●
●
等差数列的图象2
(2)数列:7,4,1,-2,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
等差数列的图象3
(3)数列:4,4,4,4,4,4,4,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
●
●
●
●
●
●
用一下
例3.某出租车的计价标准为1.2元/km,起步价为10元,即最初的4km(不含4千米)计费10元。如果某人乘坐该市的出租车去往14km处的目的地,且一路畅通,等候时间为0,需要支付多少车费?
从函数的角度来看等差数列通项公式:
所以等差数列通项公式也可以表示为:
通项公式:
③推导等差数列通项公式的方法叫做
法.
递推
每一项与
它前一项的差
二、学习新课
㈠等差数列
如果一个数列从第2项起,
等于同一个常数.
.
.
.
.
.
【说明】①数列{
an
}为等差数列?
;
an+1-an=d
或an+1=an+d
d
=an+1-an
②公差是
的常数;
唯一
an=a1+(n-1)d
等差数列各项对应的点都在同一条直线上.
直线的一般形式:
等差数列的通项公式为:
等差数列的图象为相应直线上的点。
小
结
本节课学习的主要内容有:
等差数列的定义
等差数列的通项公式
本节课的能力要求是:
(1)理解等差数列的概念;
(2)掌握等差数列的通项公式;
(3)
能用公式解决一些简单的问题.
温故知新
数列有哪些表示方法?
数列与函数的关系?
你还记得吗?
研究发现我国儿童年龄在2-12周岁之间,其标准的身高、体重大致成规律性变化:
你能预测12岁儿童的身高和体重吗?
相差7
年龄
2
3
4
5
6
…
11
12
身高(cm)
84
91
98
105
112
…
147
体重(kg)
12
14
16
18
20
…
30
相差2
154
32
(1)84,91,98,105,112,…,147,154.
(2)12,14,16,18,20,…,30,32
1896年,雅典举行第一届现代奥运会,到2012年的伦敦奥运会已经是第30届奥运会。
(3)1896,1900,1904,…,2008,2012,(
)
你能预测出第31届奥运会的时间吗?
2016
相差4
五
(4)
4,
7,
10,
13,
16,
19,
22.
星期
路程(km)
一
二
三
4
7
10
日
22
四
13
16
六
19
相差3
为迎接世界田径锦标赛,刘翔的教练为他安排了为期一周的赛前热身,逐渐加大慢跑路程
(1)
84,91,98,105,112,…,147,154.
(2)
12,14,16,18,20,…,30,32
(3)
1996,2000,2004,2008,2012,2016
(4)
4,
7,
10,
13,
16,
19,
22.
请问:它们有什么共同特点?
共同特点:从第2项起,每一项与它的前一项的差等于同一个常数。
定义:如果一个数列从第2项起,每一项与它的前一项
的差都等于同一个常数,那么这个数列就叫做等差数列.
这个常数叫做等差数列的公差,公差通常用
d
表示.
d=7
d=2
d=4
d=3
是
不是
不是
判断下列各组数列中哪些是等差数列,哪些不是?如果是,写出首项a1和公差d,
如果不是,说明理由。
(1)1,3,5,7,…
(2)9,6,3,0,-3…
(3)-8,-6,-4,-2,0,…
(4)3,3,3,3,…
(6)15,12,10,8,6,…
小结:判断一个数列是不是等差数列,主要是由定义进行判断:
an+1-an是不是同一个常数?
是
是
是
a1=1,d=2
a1=9,d=-3
a1=-8,d=2
a1=3,d=0
在如下的两个数之间,插入一个什么数后这三个数就会成为一个等差数列:
(1)2
,(
)
,
4
(2)-12,(
)
,0
3
-6
如果在a与b中间插入一个数A,使a,A,b成等差数列,那么A叫做a与b的等差中项。
(
3
)
,
(
)
,
通项公式:
如果一个数列
是等差数列,它的公差是d,那么
…,
…
例1
(1)
求等差数列8,5,2,…,的第20项。
解:
(2)-401是不是等差数列-5,-9,-13…的项?如果是,是第几项?
解:
因此,
解得
,
20
,
3
8
5
,
8
1
=
-
=
-
=
=
n
d
a
Q
用一下
在等差数列中,已知a5=10,a12=31,
解:由题意可知
即这个等差数列的首项是-2,公差是3.
求首项a1与公差d.
解得:
说明:由此可以看到:已知等差数列的两项就
可以确定这个数列.
练一练
练一练
在等差数列中
例2、已知数列的通项公式为
,其中p,q是常数,那么这种数列是否一定是等差数列?如果是,其首项与公差是什么?
探究:在坐标系中画出下列数列的图像
(1)数列:-2,0,2,4,6,8,10,…
(2)数列:7,4,1,-2,…
(3)数列:4,4,4,4,4,4,4,…
等差数列的图象1
(1)数列:-2,0,2,4,6,8,10,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
●
●
●
等差数列的图象2
(2)数列:7,4,1,-2,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
等差数列的图象3
(3)数列:4,4,4,4,4,4,4,…
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
●
●
●
●
●
●
●
●
●
●
用一下
例3.某出租车的计价标准为1.2元/km,起步价为10元,即最初的4km(不含4千米)计费10元。如果某人乘坐该市的出租车去往14km处的目的地,且一路畅通,等候时间为0,需要支付多少车费?
从函数的角度来看等差数列通项公式:
所以等差数列通项公式也可以表示为:
通项公式:
③推导等差数列通项公式的方法叫做
法.
递推
每一项与
它前一项的差
二、学习新课
㈠等差数列
如果一个数列从第2项起,
等于同一个常数.
.
.
.
.
.
【说明】①数列{
an
}为等差数列?
;
an+1-an=d
或an+1=an+d
d
=an+1-an
②公差是
的常数;
唯一
an=a1+(n-1)d
等差数列各项对应的点都在同一条直线上.
直线的一般形式:
等差数列的通项公式为:
等差数列的图象为相应直线上的点。
小
结
本节课学习的主要内容有:
等差数列的定义
等差数列的通项公式
本节课的能力要求是:
(1)理解等差数列的概念;
(2)掌握等差数列的通项公式;
(3)
能用公式解决一些简单的问题.
