镶嵌
图片预览







文档简介
(共37张PPT)
用一些不重叠摆放的多边形把平面的一部分完全覆盖(既无缝隙又不重叠),通常把这类问题叫做用多边形覆盖平面(或平面镶嵌)。
仅用一种正多边形镶嵌,哪几种正
多边形能镶嵌成一个平面?
探究问题(一)
(1)用正三角形能否镶嵌?
结论:用正三角形可以镶嵌
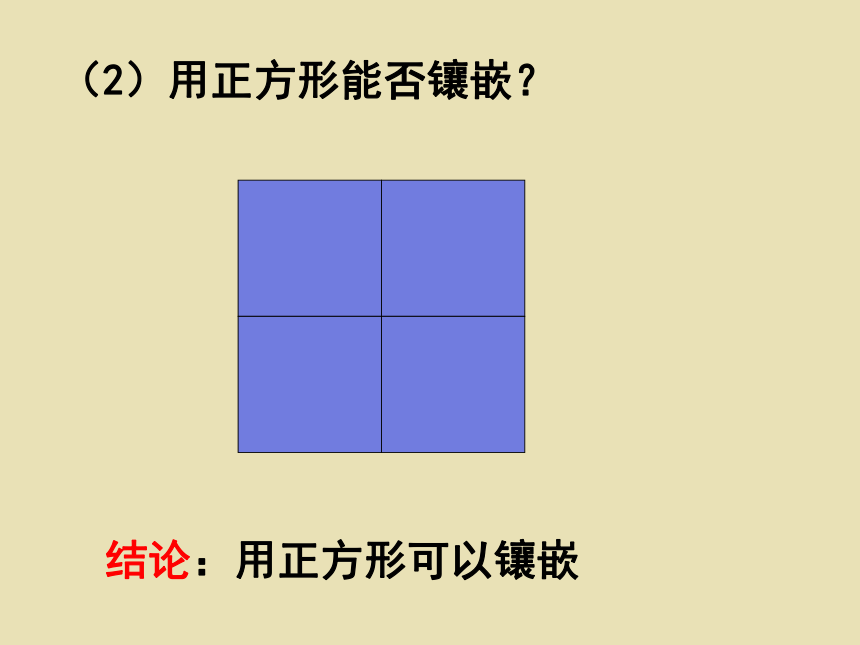
(2)用正方形能否镶嵌?
结论:用正方形可以镶嵌
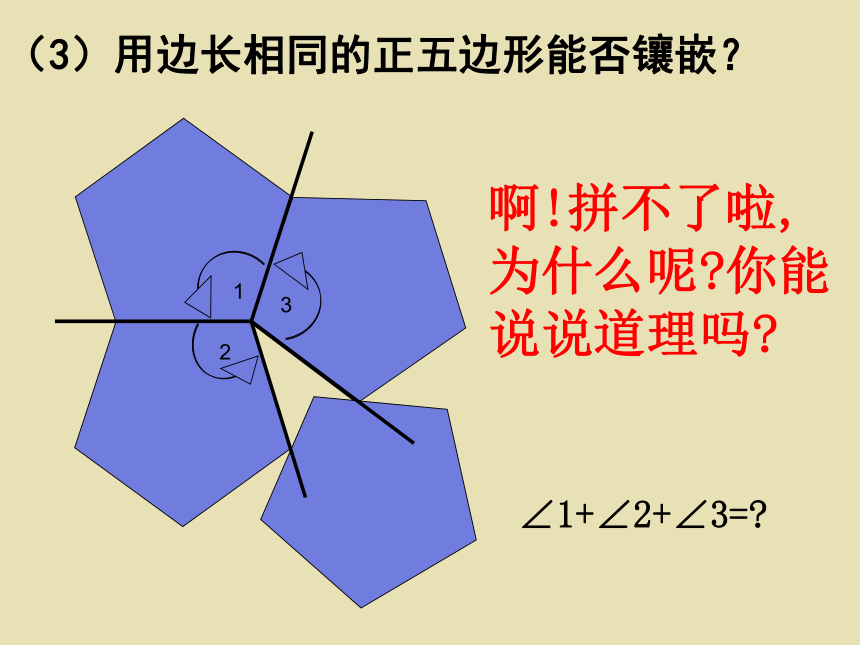
啊!拼不了啦,为什么呢 你能说说道理吗
1
2
3
∠1+∠2+∠3=
(3)用边长相同的正五边形能否镶嵌?
(4)用正六边形能否镶嵌?
结论:用边长相同的正六边形可以镶嵌
。
k ·
(n-2)×180
n
= 360
。
k(n-2)=2n
k=6
n=3
k=4
n=4
k=3
n=6
设在一个顶点处有 k 个正 n 边形的角,则有:
∵ k 为正整数, n 为大于等于 3 的正整数
∴解为
用正多边形镶嵌成一个平面的关键: 360°是否是这种正多边形的一个内角的整数倍。
只用一种正多边形能进行镶嵌的有:正三角形、正方形、正六边形
用两种正多边形镶嵌,哪些能
镶嵌成一个平面
探究问题(二)
2m+3n=12
m=3
n=2
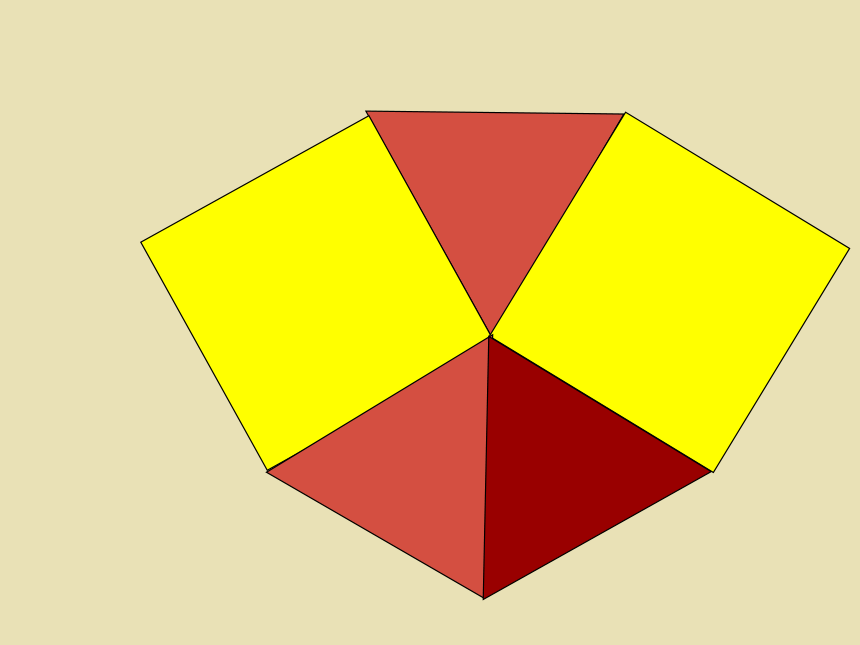
m·60 +n·90 =360
。
。
。
设在一个顶点处有 m 个正三角
形的角,n 个正方形的角,则:
∵ m,n 为正整数
∴解为
m+2n=6
m=2
n=2
m=4
n=1
m·60 +n·120 =360
。
。
。
设在一个顶点周围有 m 个正三角形的角,n 个正六边形的角,
则有
∵ m,n 为正整数
∴解为
2m+5n=12
m=1
n=2
m·60 +n·150 =360
。
。
。
设在一个顶点周围有 m 个正三角形的角,n 个正十二边形
的角,则有
∵ m,n 为正整数
∴解为
2m+3n=8
m=1
n=2
m·90 +n·135 =360
。
。
。
设在一个顶点周围有个 m 正四边形的角,n 个正八边形
的角,则有
∵ m,n 为正整数
∴解为
设在一个顶点周围有 m 个正五边形的角,n 个正十边形的角,则有
3m+4n=10
m=2
n=1
m·108 +n·144 =360
。
。
。
∵ m,n 为正整数
∴解为
用三种正多边形镶嵌,哪些能
镶嵌成一个平面?
探究问题(三)
1 、平面镶嵌的定义
2 、镶嵌的意义、条件、作用、方法
3 、关注身边的数学
4 、关注数学中的美
总结:
1、用一些形状相同、大小相等的任意三角形可以平面镶嵌吗?如果能三角形如何镶嵌呢
如图,四边形ABCD中,因为∠A+∠B+∠C+ ∠D = 360°,所以
用四边形也可以作平面镶嵌
A
B
D
C
2、任意四边形呢
那么四边形如何镶嵌呢 请看!
因为任意四边形的内角和都等于360 。把相同四边形的顶点拼结在一起,能容纳4个角,这个角刚好是等于四边形的4个内角,这样就可以无重叠无空隙地拼接在一起。
用一些不重叠摆放的多边形把平面的一部分完全覆盖(既无缝隙又不重叠),通常把这类问题叫做用多边形覆盖平面(或平面镶嵌)。
仅用一种正多边形镶嵌,哪几种正
多边形能镶嵌成一个平面?
探究问题(一)
(1)用正三角形能否镶嵌?
结论:用正三角形可以镶嵌
(2)用正方形能否镶嵌?
结论:用正方形可以镶嵌
啊!拼不了啦,为什么呢 你能说说道理吗
1
2
3
∠1+∠2+∠3=
(3)用边长相同的正五边形能否镶嵌?
(4)用正六边形能否镶嵌?
结论:用边长相同的正六边形可以镶嵌
。
k ·
(n-2)×180
n
= 360
。
k(n-2)=2n
k=6
n=3
k=4
n=4
k=3
n=6
设在一个顶点处有 k 个正 n 边形的角,则有:
∵ k 为正整数, n 为大于等于 3 的正整数
∴解为
用正多边形镶嵌成一个平面的关键: 360°是否是这种正多边形的一个内角的整数倍。
只用一种正多边形能进行镶嵌的有:正三角形、正方形、正六边形
用两种正多边形镶嵌,哪些能
镶嵌成一个平面
探究问题(二)
2m+3n=12
m=3
n=2
m·60 +n·90 =360
。
。
。
设在一个顶点处有 m 个正三角
形的角,n 个正方形的角,则:
∵ m,n 为正整数
∴解为
m+2n=6
m=2
n=2
m=4
n=1
m·60 +n·120 =360
。
。
。
设在一个顶点周围有 m 个正三角形的角,n 个正六边形的角,
则有
∵ m,n 为正整数
∴解为
2m+5n=12
m=1
n=2
m·60 +n·150 =360
。
。
。
设在一个顶点周围有 m 个正三角形的角,n 个正十二边形
的角,则有
∵ m,n 为正整数
∴解为
2m+3n=8
m=1
n=2
m·90 +n·135 =360
。
。
。
设在一个顶点周围有个 m 正四边形的角,n 个正八边形
的角,则有
∵ m,n 为正整数
∴解为
设在一个顶点周围有 m 个正五边形的角,n 个正十边形的角,则有
3m+4n=10
m=2
n=1
m·108 +n·144 =360
。
。
。
∵ m,n 为正整数
∴解为
用三种正多边形镶嵌,哪些能
镶嵌成一个平面?
探究问题(三)
1 、平面镶嵌的定义
2 、镶嵌的意义、条件、作用、方法
3 、关注身边的数学
4 、关注数学中的美
总结:
1、用一些形状相同、大小相等的任意三角形可以平面镶嵌吗?如果能三角形如何镶嵌呢
如图,四边形ABCD中,因为∠A+∠B+∠C+ ∠D = 360°,所以
用四边形也可以作平面镶嵌
A
B
D
C
2、任意四边形呢
那么四边形如何镶嵌呢 请看!
因为任意四边形的内角和都等于360 。把相同四边形的顶点拼结在一起,能容纳4个角,这个角刚好是等于四边形的4个内角,这样就可以无重叠无空隙地拼接在一起。
