7.5正态分布-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册课件(26张PPT)
文档属性
| 名称 | 7.5正态分布-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册课件(26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 10:19:04 | ||
图片预览






文档简介
7.5
正 态 分 布
高二数学选择性必修 第三册 第七章 随机变量及其分布
学习目标
1.利用实际问题的频率分布直方图,了解正态曲线的特征、意义以及正态曲线的性质;
2.会根据正态曲线的性质求随机变量在某一区间的概率;
3.核心素养: 数学抽象、直观想象、数学运算.
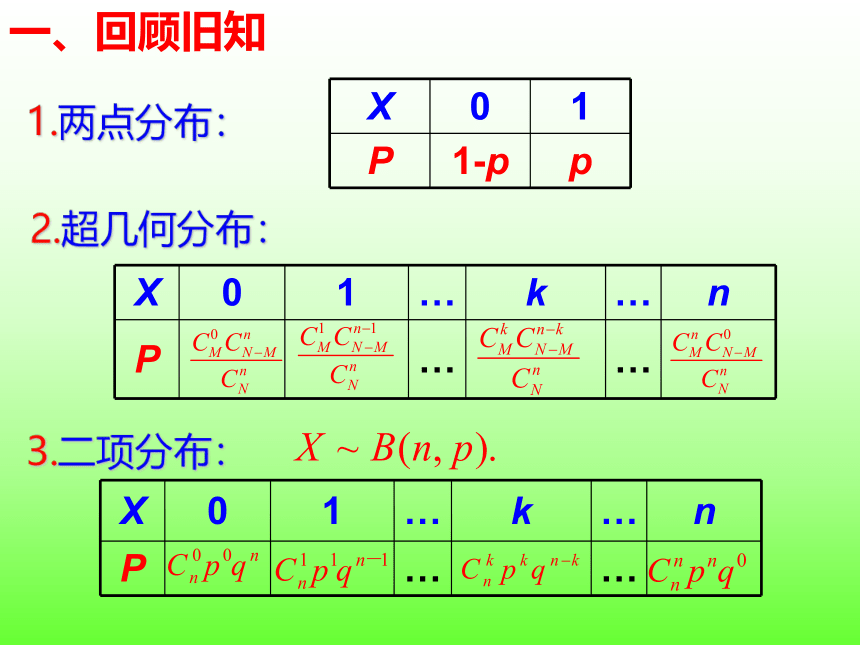
1.两点分布:
X
0
1
P
1-p
p
2.超几何分布:
3.二项分布:
X
0
1
…
k
…
n
P
…
…
X
0
1
…
k
…
n
P
…
…
一、回顾旧知
4.连续性随机变量
连续型随机变量是指可以取某一区间的一切
值的随机变量,又称作连续型随机变量
但取一点的概率为0
二、探究新知
1.问题:自动流水线包装的食盐,每袋标准质量为400 g. 由于各种不可控的因素,任意抽取一袋食盐,它的质量与标准质量之间或多 或少会存在一定的误差(实际质量减去标准质量). 用 X 表示这种误差,则X 是一个连续型随机变量 . 检测人员在一次产品检验中, 随机抽取了100袋食盐,获得误差 X (单位:g)的观测值如下:
-0.6
-1.4
-0.7
3.3
-2.9
-5.2
1.4
0.1
4.4
0.9
-2.6
-3.4
-0.7
-3.2
-1.7
2.9
0.6
1.7
2.9
1.2
0.5
-3.7
2.7
1.1
-3.0
-2.6
-1.9
1.7
2.6
0.4
2.6
-2.0
-0.2
1.8
-0.7
-1.3
-0.5
-1.3
0.2
-2.1
2.4
-1.5
-0.4
3.8
-0.1
1.5
0.3
-1.8
0.0
2.5
3.5
-4.2
-1.0
-0.2
0.1
0.9
1.1
2.2
0.9
-0.6
-4.4
-1.1
3.9
-1.0
-0.6
1.7
0.3
-2.4
-0.1
-1.7
-0.5
-0.8
1.7
1.4
4.4
1.2
-1.8
-3.1
-2.1
-1.6
2.2
0.3
4.8
-0.8
-3.5
-2.7
3.8
1.4
-3.5
-0.9
-2.2
-0.7
-1.3
1.5
-1.5
-2.2
1.0
1.3
1.7
-0.9
(1).如何描述这100个样本误差数据的分布?
(2).如何构建适当的概率模型刻画误差X的分布?
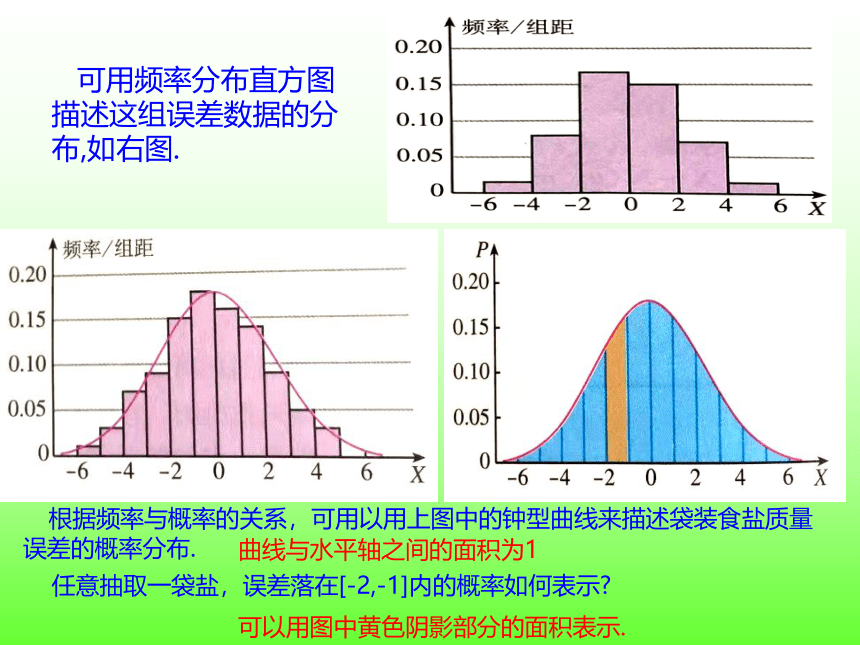
可用频率分布直方图描述这组误差数据的分布,如右图.
根据频率与概率的关系,可用以用上图中的钟型曲线来描述袋装食盐质量误差的概率分布.
曲线与水平轴之间的面积为1
任意抽取一袋盐,误差落在[-2,-1]内的概率如何表示?
可以用图中黄色阴影部分的面积表示.
2.正态密度曲线(简称正态曲线)
0
Y
X
相应的函数解析式为:
称为正态密度函数
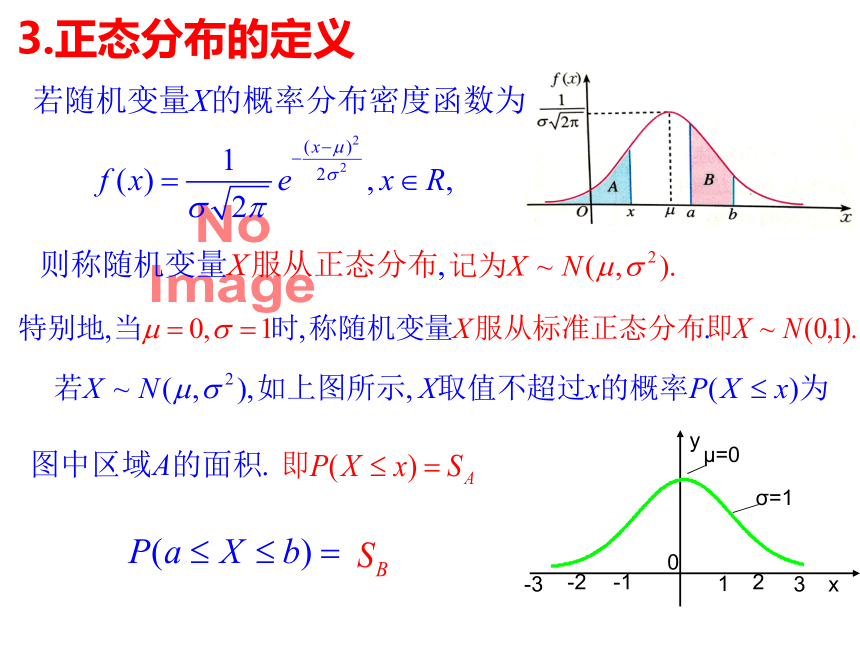
3.正态分布的定义
y
0
1
2
-1
-2
x
-3
3
μ=0
σ=1
正态分布在概率和统计中占有重要地位,它广泛
存在于自然现象、生产和生活实践之中.
在现实生活中,很多随机变量都服从或近似服从
正态分布.
例如,某些物理量的测量误差
某一地区同年龄人群的身高、体重、肺活量等
一定条件下生长的小麦的株高、穗长、单位面积产量
自动流水线生产的各种产品的质量指标(如零件的尺寸、纤维的纤度、电容器的电容)
某地每年7月的平均气温、平均湿度、降水量等
一般都近似服从正态分布
4.例1.下列函数是正态密度函数的是( )
A.
B.
C.
D.
B
具有两头低、中间高、左右对称的基本特征
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
5.正态曲线的性质
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
(1)对称性:曲线是单峰的,它关于直线x=μ对称.
6.正态曲线的性质
(2)最值性:曲线在x=μ处达到峰值(最高点)
x=m
x=m
x=m
(3)当 无限增大时,曲线无限接近 轴.
7.参数 含义及对正态曲线的形状的影响
一个正态分布由参数 和 完全确定,这两个参数对
正态曲线的形状有何影响?它们反映正态分布的哪些特征?
?3
?1
?2
σ=1
μ= -1
μ=0
μ=1
若 固定, 随 值的变化而沿x轴平移, 故 称为位置参数;
x
y
(1).当参数 取定值时
?
? =0.5
? =1
?=2
μ=0
若 固定, 大时, 曲线“矮而胖”; 小时, 曲线“瘦而高”, 故称 为
形状参数.
所以σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
x
y
(2).当参数 取定值时
三、巩固新知
1.例2.
解:
26
30
34
38
t
y
(2)如右图
1.例2.
26
30
34
38
t
y
2.变式训练1
3.正态分布的 原则
4.例3.在某次数学考试中,考生的成绩X服从正态分布X~N(90,100).
(1).求考试成绩X位于区间(70,110)上的概率是多少?
(2).若此次考试共有2000名考生,试估计考试成绩在
(80,100)间的考生大约有多少人?
解:(1)依题意,X~N(90,100),
即考试成绩在(80,100)间的概率为0.6827.
考试成绩在(80,100)间的考生大约有
5.例4.若X~N(5,1),求P(6解:因为X~N(5,1),
故正态密度曲线关于直线 x=5 对称,
1).若X~N(μ,σ2),问X位于区域(μ,μ+σ)内的概率是多少?
解:由正态曲线的对称性可得,
6.变式训练2
四、课堂小结
1.正态曲线及正态密度函数
2.正态分布
3.正态曲线的性质
(1)对称性:曲线是单峰的,它关于直线x=μ对称.
(2)最值性:曲线在x=μ处达到峰值(最高点)
(3)当 无限增大时,曲线无限接近 轴.
4.正态分布的 原则
作业: 课本P87 习题7.5 1,2,3题
正 态 分 布
高二数学选择性必修 第三册 第七章 随机变量及其分布
学习目标
1.利用实际问题的频率分布直方图,了解正态曲线的特征、意义以及正态曲线的性质;
2.会根据正态曲线的性质求随机变量在某一区间的概率;
3.核心素养: 数学抽象、直观想象、数学运算.
1.两点分布:
X
0
1
P
1-p
p
2.超几何分布:
3.二项分布:
X
0
1
…
k
…
n
P
…
…
X
0
1
…
k
…
n
P
…
…
一、回顾旧知
4.连续性随机变量
连续型随机变量是指可以取某一区间的一切
值的随机变量,又称作连续型随机变量
但取一点的概率为0
二、探究新知
1.问题:自动流水线包装的食盐,每袋标准质量为400 g. 由于各种不可控的因素,任意抽取一袋食盐,它的质量与标准质量之间或多 或少会存在一定的误差(实际质量减去标准质量). 用 X 表示这种误差,则X 是一个连续型随机变量 . 检测人员在一次产品检验中, 随机抽取了100袋食盐,获得误差 X (单位:g)的观测值如下:
-0.6
-1.4
-0.7
3.3
-2.9
-5.2
1.4
0.1
4.4
0.9
-2.6
-3.4
-0.7
-3.2
-1.7
2.9
0.6
1.7
2.9
1.2
0.5
-3.7
2.7
1.1
-3.0
-2.6
-1.9
1.7
2.6
0.4
2.6
-2.0
-0.2
1.8
-0.7
-1.3
-0.5
-1.3
0.2
-2.1
2.4
-1.5
-0.4
3.8
-0.1
1.5
0.3
-1.8
0.0
2.5
3.5
-4.2
-1.0
-0.2
0.1
0.9
1.1
2.2
0.9
-0.6
-4.4
-1.1
3.9
-1.0
-0.6
1.7
0.3
-2.4
-0.1
-1.7
-0.5
-0.8
1.7
1.4
4.4
1.2
-1.8
-3.1
-2.1
-1.6
2.2
0.3
4.8
-0.8
-3.5
-2.7
3.8
1.4
-3.5
-0.9
-2.2
-0.7
-1.3
1.5
-1.5
-2.2
1.0
1.3
1.7
-0.9
(1).如何描述这100个样本误差数据的分布?
(2).如何构建适当的概率模型刻画误差X的分布?
可用频率分布直方图描述这组误差数据的分布,如右图.
根据频率与概率的关系,可用以用上图中的钟型曲线来描述袋装食盐质量误差的概率分布.
曲线与水平轴之间的面积为1
任意抽取一袋盐,误差落在[-2,-1]内的概率如何表示?
可以用图中黄色阴影部分的面积表示.
2.正态密度曲线(简称正态曲线)
0
Y
X
相应的函数解析式为:
称为正态密度函数
3.正态分布的定义
y
0
1
2
-1
-2
x
-3
3
μ=0
σ=1
正态分布在概率和统计中占有重要地位,它广泛
存在于自然现象、生产和生活实践之中.
在现实生活中,很多随机变量都服从或近似服从
正态分布.
例如,某些物理量的测量误差
某一地区同年龄人群的身高、体重、肺活量等
一定条件下生长的小麦的株高、穗长、单位面积产量
自动流水线生产的各种产品的质量指标(如零件的尺寸、纤维的纤度、电容器的电容)
某地每年7月的平均气温、平均湿度、降水量等
一般都近似服从正态分布
4.例1.下列函数是正态密度函数的是( )
A.
B.
C.
D.
B
具有两头低、中间高、左右对称的基本特征
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
5.正态曲线的性质
0
1
2
-1
-2
x
y
-3
μ= -1
σ=0.5
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
0
1
2
-1
-2
x
y
-3
3
4
μ=1
σ=2
(1)对称性:曲线是单峰的,它关于直线x=μ对称.
6.正态曲线的性质
(2)最值性:曲线在x=μ处达到峰值(最高点)
x=m
x=m
x=m
(3)当 无限增大时,曲线无限接近 轴.
7.参数 含义及对正态曲线的形状的影响
一个正态分布由参数 和 完全确定,这两个参数对
正态曲线的形状有何影响?它们反映正态分布的哪些特征?
?3
?1
?2
σ=1
μ= -1
μ=0
μ=1
若 固定, 随 值的变化而沿x轴平移, 故 称为位置参数;
x
y
(1).当参数 取定值时
?
? =0.5
? =1
?=2
μ=0
若 固定, 大时, 曲线“矮而胖”; 小时, 曲线“瘦而高”, 故称 为
形状参数.
所以σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
x
y
(2).当参数 取定值时
三、巩固新知
1.例2.
解:
26
30
34
38
t
y
(2)如右图
1.例2.
26
30
34
38
t
y
2.变式训练1
3.正态分布的 原则
4.例3.在某次数学考试中,考生的成绩X服从正态分布X~N(90,100).
(1).求考试成绩X位于区间(70,110)上的概率是多少?
(2).若此次考试共有2000名考生,试估计考试成绩在
(80,100)间的考生大约有多少人?
解:(1)依题意,X~N(90,100),
即考试成绩在(80,100)间的概率为0.6827.
考试成绩在(80,100)间的考生大约有
5.例4.若X~N(5,1),求P(6
故正态密度曲线关于直线 x=5 对称,
1).若X~N(μ,σ2),问X位于区域(μ,μ+σ)内的概率是多少?
解:由正态曲线的对称性可得,
6.变式训练2
四、课堂小结
1.正态曲线及正态密度函数
2.正态分布
3.正态曲线的性质
(1)对称性:曲线是单峰的,它关于直线x=μ对称.
(2)最值性:曲线在x=μ处达到峰值(最高点)
(3)当 无限增大时,曲线无限接近 轴.
4.正态分布的 原则
作业: 课本P87 习题7.5 1,2,3题
