9.1.2分层随机抽样-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习Word含解析
文档属性
| 名称 | 9.1.2分层随机抽样-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习Word含解析 |

|
|
| 格式 | doc | ||
| 文件大小 | 841.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 00:00:00 | ||
图片预览



文档简介
9.1.2分层随机抽样 同步练习
一.选择题
1.要从1 000个球中抽取100个进行抽样分析,其中红球共有50个,如果用分层抽样的方法对球进行抽样,则应抽取红球
A.33个 B.20个 C.5个 D.10个
2.某校为了解高一学生的生涯规划情况,在高一年级6个班级中任选两个班级,并在所选的班级中按男女比例抽取样本,则应采用的抽样方法是
A.简单随机抽样
B.分层抽样
C.先用分层抽样,再用随机数表法
D.先用抽签法,再用分层抽样
3.某校高中生共有900人,其中高一年级有300人,高二年级有200人,高三年级有400人,现采用分层抽样方法抽取一个容量为45的样本,则高一、高二、高三年级抽取的人数分别为
A.10,15,20 B.15,15,15 C.20,5,20 D.15,10,20
4.某学院的,,三个专业共有1200名学生,为了调查这些学生勤工俭学的情况,拟采用分层抽样的方法抽取一个容量为120的样本.已知该学院的专业有380名学生,专业有420名学生,则在该学院的专业应抽取的学生是
A.42名 B.38名 C.40名 D.120名
5.某中学有高中生3000人,初中生2000人,高中生中男生、女生人数之比为,初中生中男生、女生人数之比为,为了解学生的学习状况,用分层抽样的方法从该校学生中抽取一个容量为的样本,已知从初中生中抽取男生12人,则从高中生中抽取的女生人数是
A.12 B.15 C.20 D.21
6.某学校高一、高二、高三共有学生3500人,其中高三学生数是高一学生数的两倍,高二学生数比高一学生数多300人,现在按的抽样比用分层抽样的方法抽取样本,则应抽取高一学生数为
A.8 B.11 C.16 D.10
7.某市新上了一批便民公共自行车,有绿色和橙黄色两种颜色,且绿色公共自行车和橙黄色公共自行车的数量比为,现在按照分层抽样的方法抽取36辆这样的公共自行车放在某校门口,则其中绿色公共自行车的辆数是
A.8 B.12 C.16 D.24
8.某工厂生产、、三种不同型号的产品,其中某月生产的产品数量之比依次为,现用分层抽样的方法抽取一个容量为120的样本,已知种型号产品抽取了45件,则
A.1 B.2 C.3 D.4
9.某运动队由足球运动员18人,篮球运动员12人,乒乓球运动员6人组成(每人只参加一项),现从这些运动员中抽取一个容量为的样本,若分别采用系统抽样法和分层抽样法,都不用剔除个体,那么样本容量的最小值为
A.6 B.12 C.18 D.24
10.某高中在校学生2000人.为了响应“阳光体育运动”号召,学校举行了跑步和登山比赛活动.每人都参加而且只参与了其中一项比赛,各年级参与比赛人数情况如表:
高一年级 高二年级 高三年级
跑步
登山
其中,全校参与登山的人数占总人数的,为了了解学生对本次活动的满意程度,现用分层抽样方式从中抽取一个100个人的样本进行调查,则高二级参与跑步的学生中应抽取
A.6人 B.12人 C.18人 D.24人
11.(多选)某工厂生产、、三种不同型号的产品,其相应产品数量之比为,现用分层抽样方法抽出一个容量为的样本,样本中型号产品有16件,则
A.此样本的容量为20 B.此样本的容量为80
C.样本中型号产品有40件 D.样本中型号产品有24件
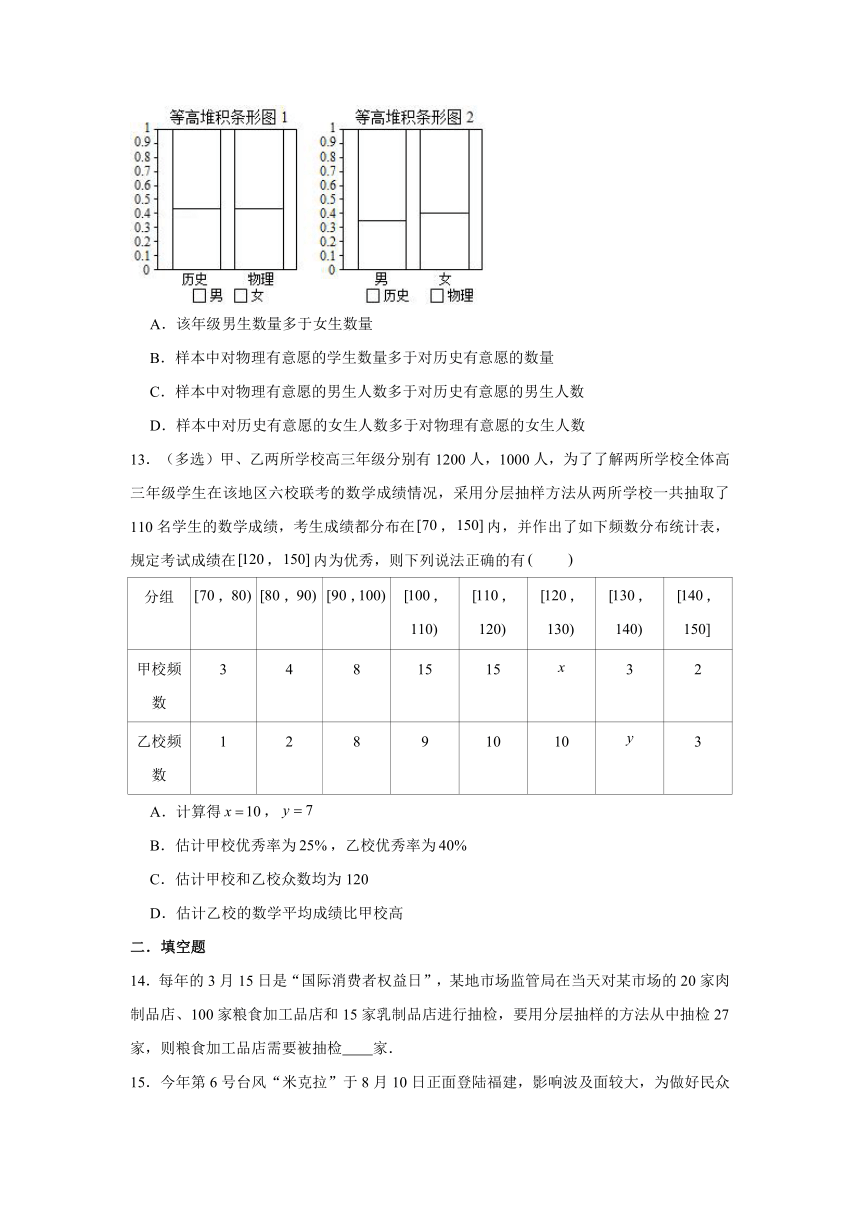
12.(多选)某中学高一年级半期考试后将进行新高考首选科目的选择,每位同学必须在“物理”、“历史”中二选一,学校采用分层抽样的方法,抽取了该年级部分男、女学生选科意愿的一份样本,并根据统计结果绘制如右两个等高堆积条形图.根据这两幅图中的信息,下列统计结论正确的是
A.该年级男生数量多于女生数量
B.样本中对物理有意愿的学生数量多于对历史有意愿的数量
C.样本中对物理有意愿的男生人数多于对历史有意愿的男生人数
D.样本中对历史有意愿的女生人数多于对物理有意愿的女生人数
13.(多选)甲、乙两所学校高三年级分别有1200人,1000人,为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩,考生成绩都分布在,内,并作出了如下频数分布统计表,规定考试成绩在,内为优秀,则下列说法正确的有
分组 , , , , , , , ,
甲校频数 3 4 8 15 15
3 2
乙校频数 1 2 8 9 10 10
3
A.计算得,
B.估计甲校优秀率为,乙校优秀率为
C.估计甲校和乙校众数均为120
D.估计乙校的数学平均成绩比甲校高
二.填空题
14.每年的3月15日是“国际消费者权益日”,某地市场监管局在当天对某市场的20家肉制品店、100家粮食加工品店和15家乳制品店进行抽检,要用分层抽样的方法从中抽检27家,则粮食加工品店需要被抽检 家.
15.今年第6号台风“米克拉”于8月10日正面登陆福建,影响波及面较大,为做好民众的安全防护工作,当地政府及有关部门做了大量的宣传及预防工作,事后某自由媒体从、、三个社区按社区人数之比,采用分层抽样的方法抽取位居民进行问卷检测,了解其对突发事件的防护等安全知识的掌握情况.若社区抽取了20位居民,则的值是 .
16.某校高一、高二、高三共有200名学生,为调查他们的体育锻炼情况,通过分层抽样获得了20名学生一周的锻炼时间,数据如表(单位:小时)
高一 6 6.5 7 7.5 8
高二 6 7 8 9 10 11 12
高三 3 4.5 6 7.5 9 10.5 12 13.5
则根据上述样本数据估计该校学生一周的锻炼时间不小于7小时的人数为 .
17.已知某地区中小学生人数和近视情况分别如图甲和乙所示.为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取的学生进行调查,则样本容量为 ;抽取的高中生中近视的人数为 .
18.某企业三月中旬生产、、三种产品共3000件,根据分层抽样的结果,企业统计员制作了如下的统计表格:
产品类别
产品数量(件 1300
样本容量 130
由于不小心,表格中、产品的有关数据已被污染看不清楚,统计员只记得产品的样本容量比产品的样本容量多10,请你根据以上信息填补表格中数据.
9.1.2分层随机抽样 同步练习答案
1.解:要从1000个球中抽取100个进行抽样分析,其中红球共有50个,
抽样比,
用分层抽样的方法对球进行抽样,则应抽取红球:个.
故选:.
2.解:某校为了解高一学生的生涯规划情况,在高一年级6个班级中任选两个班级,
利用抽签法,
并在所选的班级中按男女比例抽取样本,
利用分层抽样法,
应采用的抽样方法是先用抽签法,再用分层抽样.
故选:.
3.解:根据题意得,用分层抽样在各层中的抽样比为,
则在高一年级抽取的人数是人,
高二年级抽取的人数是人,
高三年级抽取的人数是人,
故选:.
4.解:专业的学生有,
由分层抽样原理,应抽取名.
故选:.
5.解:某中学有高中生3000人,初中生2000人,
高中生中男生、女生人数之比为,初中生中男生、女生人数之比为,
高中生男生有人,初中男生有:人,
从初中生中抽取男生12人,设从高中生中抽取的女生人数为,
,解得,
故选:.
6.解:设高一学生有人,则高三有,高二有,
高一、高二、高三共有学生3500人,
,
,
按的抽样比用分层抽样的方法抽取样本,
应抽取高一学生数为
故选:.
7.解:根据题意,绿色公共自行车和橙黄色公共自行车的数量比为,
所以样本中绿色公共自行车和橙黄色公共自行车的数量比也为,
所以绿色公共自行车的辆数为,
故选:.
8.解:某工厂生产、、三种不同型号的产品,
其中某月生产的产品数量之比依次为,
现用分层抽样的方法抽取一个容量为120的样本,
种型号产品抽取了45件,则,
解得.
故选:.
9.解:总体容量,则系统抽样的间隔为,采用分层抽样的比例是,分层抽样乒乓球运动员人数为,篮球运动员人数为,足球运动员人数为,可知应为6的倍数,36的约数,故样本容量最小的.
故选:.
10.解:根据题意可知样本中参与跑步的人数为人,所以高二级参与跑步的学生中应抽取的人数为人.
故选:.
11.解:工厂生产、、三种不同型号的产品,其相应产品数量之比为,
现用分层抽样方法抽出一个容量为的样本,样本中型号产品有16件,
设样本为,则,故错误,正确;
样本中型号产品有:件,故正确,错误.
故选:.
12.解:由图2知,样本中的女生数量多于男生数量,
样本中的男生、女生均偏爱理科,故错误,正确;
由图1知,样本中有理科意愿的学生数量多于有文科意愿的学生数量,故正确,错误,
故选:.
13.解::甲校抽取的人数为:人,乙校抽取人数为人,所以,解得;
同理可得可得,所以正确;
,由表可得甲校的优秀人数为,所以优秀率为,
乙校的优秀人数,所以乙校的优秀率为所以正确;
甲的众数是105和115,乙的众数115和125,所以不正确;
:甲校的平均成绩为,
乙校的平均成绩为,所以正确,
故选:.
14.解:根据分层抽样原理知,粮食加工品店需要被抽检(家.
故答案为:20.
15.解:根据分层抽样方法原理知,
,
解得,
所以的值是55.
故答案为:55.
16.解:样本数据中该校学生一周的锻炼时间不小于7小时的人数为(人,
估计该校学生一周的锻炼时间不小于7小时的人数为(人.
故答案为:140.
17.解:样本容量为:;
抽取的高中生人数为:.
故答案为:300;30.
18.解:设样本的总容量为,则,
.
产品和产品在样本中共有(件.
设产品的样本容量为,
则,.
产品的数量为.
产品的数量为.
故:
产品类别
产品数量(件 900 1300 800
样本容量 90 130 80
一.选择题
1.要从1 000个球中抽取100个进行抽样分析,其中红球共有50个,如果用分层抽样的方法对球进行抽样,则应抽取红球
A.33个 B.20个 C.5个 D.10个
2.某校为了解高一学生的生涯规划情况,在高一年级6个班级中任选两个班级,并在所选的班级中按男女比例抽取样本,则应采用的抽样方法是
A.简单随机抽样
B.分层抽样
C.先用分层抽样,再用随机数表法
D.先用抽签法,再用分层抽样
3.某校高中生共有900人,其中高一年级有300人,高二年级有200人,高三年级有400人,现采用分层抽样方法抽取一个容量为45的样本,则高一、高二、高三年级抽取的人数分别为
A.10,15,20 B.15,15,15 C.20,5,20 D.15,10,20
4.某学院的,,三个专业共有1200名学生,为了调查这些学生勤工俭学的情况,拟采用分层抽样的方法抽取一个容量为120的样本.已知该学院的专业有380名学生,专业有420名学生,则在该学院的专业应抽取的学生是
A.42名 B.38名 C.40名 D.120名
5.某中学有高中生3000人,初中生2000人,高中生中男生、女生人数之比为,初中生中男生、女生人数之比为,为了解学生的学习状况,用分层抽样的方法从该校学生中抽取一个容量为的样本,已知从初中生中抽取男生12人,则从高中生中抽取的女生人数是
A.12 B.15 C.20 D.21
6.某学校高一、高二、高三共有学生3500人,其中高三学生数是高一学生数的两倍,高二学生数比高一学生数多300人,现在按的抽样比用分层抽样的方法抽取样本,则应抽取高一学生数为
A.8 B.11 C.16 D.10
7.某市新上了一批便民公共自行车,有绿色和橙黄色两种颜色,且绿色公共自行车和橙黄色公共自行车的数量比为,现在按照分层抽样的方法抽取36辆这样的公共自行车放在某校门口,则其中绿色公共自行车的辆数是
A.8 B.12 C.16 D.24
8.某工厂生产、、三种不同型号的产品,其中某月生产的产品数量之比依次为,现用分层抽样的方法抽取一个容量为120的样本,已知种型号产品抽取了45件,则
A.1 B.2 C.3 D.4
9.某运动队由足球运动员18人,篮球运动员12人,乒乓球运动员6人组成(每人只参加一项),现从这些运动员中抽取一个容量为的样本,若分别采用系统抽样法和分层抽样法,都不用剔除个体,那么样本容量的最小值为
A.6 B.12 C.18 D.24
10.某高中在校学生2000人.为了响应“阳光体育运动”号召,学校举行了跑步和登山比赛活动.每人都参加而且只参与了其中一项比赛,各年级参与比赛人数情况如表:
高一年级 高二年级 高三年级
跑步
登山
其中,全校参与登山的人数占总人数的,为了了解学生对本次活动的满意程度,现用分层抽样方式从中抽取一个100个人的样本进行调查,则高二级参与跑步的学生中应抽取
A.6人 B.12人 C.18人 D.24人
11.(多选)某工厂生产、、三种不同型号的产品,其相应产品数量之比为,现用分层抽样方法抽出一个容量为的样本,样本中型号产品有16件,则
A.此样本的容量为20 B.此样本的容量为80
C.样本中型号产品有40件 D.样本中型号产品有24件
12.(多选)某中学高一年级半期考试后将进行新高考首选科目的选择,每位同学必须在“物理”、“历史”中二选一,学校采用分层抽样的方法,抽取了该年级部分男、女学生选科意愿的一份样本,并根据统计结果绘制如右两个等高堆积条形图.根据这两幅图中的信息,下列统计结论正确的是
A.该年级男生数量多于女生数量
B.样本中对物理有意愿的学生数量多于对历史有意愿的数量
C.样本中对物理有意愿的男生人数多于对历史有意愿的男生人数
D.样本中对历史有意愿的女生人数多于对物理有意愿的女生人数
13.(多选)甲、乙两所学校高三年级分别有1200人,1000人,为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩,考生成绩都分布在,内,并作出了如下频数分布统计表,规定考试成绩在,内为优秀,则下列说法正确的有
分组 , , , , , , , ,
甲校频数 3 4 8 15 15
3 2
乙校频数 1 2 8 9 10 10
3
A.计算得,
B.估计甲校优秀率为,乙校优秀率为
C.估计甲校和乙校众数均为120
D.估计乙校的数学平均成绩比甲校高
二.填空题
14.每年的3月15日是“国际消费者权益日”,某地市场监管局在当天对某市场的20家肉制品店、100家粮食加工品店和15家乳制品店进行抽检,要用分层抽样的方法从中抽检27家,则粮食加工品店需要被抽检 家.
15.今年第6号台风“米克拉”于8月10日正面登陆福建,影响波及面较大,为做好民众的安全防护工作,当地政府及有关部门做了大量的宣传及预防工作,事后某自由媒体从、、三个社区按社区人数之比,采用分层抽样的方法抽取位居民进行问卷检测,了解其对突发事件的防护等安全知识的掌握情况.若社区抽取了20位居民,则的值是 .
16.某校高一、高二、高三共有200名学生,为调查他们的体育锻炼情况,通过分层抽样获得了20名学生一周的锻炼时间,数据如表(单位:小时)
高一 6 6.5 7 7.5 8
高二 6 7 8 9 10 11 12
高三 3 4.5 6 7.5 9 10.5 12 13.5
则根据上述样本数据估计该校学生一周的锻炼时间不小于7小时的人数为 .
17.已知某地区中小学生人数和近视情况分别如图甲和乙所示.为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取的学生进行调查,则样本容量为 ;抽取的高中生中近视的人数为 .
18.某企业三月中旬生产、、三种产品共3000件,根据分层抽样的结果,企业统计员制作了如下的统计表格:
产品类别
产品数量(件 1300
样本容量 130
由于不小心,表格中、产品的有关数据已被污染看不清楚,统计员只记得产品的样本容量比产品的样本容量多10,请你根据以上信息填补表格中数据.
9.1.2分层随机抽样 同步练习答案
1.解:要从1000个球中抽取100个进行抽样分析,其中红球共有50个,
抽样比,
用分层抽样的方法对球进行抽样,则应抽取红球:个.
故选:.
2.解:某校为了解高一学生的生涯规划情况,在高一年级6个班级中任选两个班级,
利用抽签法,
并在所选的班级中按男女比例抽取样本,
利用分层抽样法,
应采用的抽样方法是先用抽签法,再用分层抽样.
故选:.
3.解:根据题意得,用分层抽样在各层中的抽样比为,
则在高一年级抽取的人数是人,
高二年级抽取的人数是人,
高三年级抽取的人数是人,
故选:.
4.解:专业的学生有,
由分层抽样原理,应抽取名.
故选:.
5.解:某中学有高中生3000人,初中生2000人,
高中生中男生、女生人数之比为,初中生中男生、女生人数之比为,
高中生男生有人,初中男生有:人,
从初中生中抽取男生12人,设从高中生中抽取的女生人数为,
,解得,
故选:.
6.解:设高一学生有人,则高三有,高二有,
高一、高二、高三共有学生3500人,
,
,
按的抽样比用分层抽样的方法抽取样本,
应抽取高一学生数为
故选:.
7.解:根据题意,绿色公共自行车和橙黄色公共自行车的数量比为,
所以样本中绿色公共自行车和橙黄色公共自行车的数量比也为,
所以绿色公共自行车的辆数为,
故选:.
8.解:某工厂生产、、三种不同型号的产品,
其中某月生产的产品数量之比依次为,
现用分层抽样的方法抽取一个容量为120的样本,
种型号产品抽取了45件,则,
解得.
故选:.
9.解:总体容量,则系统抽样的间隔为,采用分层抽样的比例是,分层抽样乒乓球运动员人数为,篮球运动员人数为,足球运动员人数为,可知应为6的倍数,36的约数,故样本容量最小的.
故选:.
10.解:根据题意可知样本中参与跑步的人数为人,所以高二级参与跑步的学生中应抽取的人数为人.
故选:.
11.解:工厂生产、、三种不同型号的产品,其相应产品数量之比为,
现用分层抽样方法抽出一个容量为的样本,样本中型号产品有16件,
设样本为,则,故错误,正确;
样本中型号产品有:件,故正确,错误.
故选:.
12.解:由图2知,样本中的女生数量多于男生数量,
样本中的男生、女生均偏爱理科,故错误,正确;
由图1知,样本中有理科意愿的学生数量多于有文科意愿的学生数量,故正确,错误,
故选:.
13.解::甲校抽取的人数为:人,乙校抽取人数为人,所以,解得;
同理可得可得,所以正确;
,由表可得甲校的优秀人数为,所以优秀率为,
乙校的优秀人数,所以乙校的优秀率为所以正确;
甲的众数是105和115,乙的众数115和125,所以不正确;
:甲校的平均成绩为,
乙校的平均成绩为,所以正确,
故选:.
14.解:根据分层抽样原理知,粮食加工品店需要被抽检(家.
故答案为:20.
15.解:根据分层抽样方法原理知,
,
解得,
所以的值是55.
故答案为:55.
16.解:样本数据中该校学生一周的锻炼时间不小于7小时的人数为(人,
估计该校学生一周的锻炼时间不小于7小时的人数为(人.
故答案为:140.
17.解:样本容量为:;
抽取的高中生人数为:.
故答案为:300;30.
18.解:设样本的总容量为,则,
.
产品和产品在样本中共有(件.
设产品的样本容量为,
则,.
产品的数量为.
产品的数量为.
故:
产品类别
产品数量(件 900 1300 800
样本容量 90 130 80
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
