9.2.3总体集中趋势的估计-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习Word含解析
文档属性
| 名称 | 9.2.3总体集中趋势的估计-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习Word含解析 |

|
|
| 格式 | doc | ||
| 文件大小 | 951.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 00:00:00 | ||
图片预览




文档简介
9.2.3总体集中趋势的估计 同步练习
一.单选题
1.已知一组数据为10,30,50,50,60,70,80.其中平均数、中位数和众数的大小关系是
A.平均数中位数众数 B.平均数中位数众数
C.中位数众数平均数 D.众数中位数平均数
2.已知数据①18,32,,14,8,12;②21,4,7,14,,11;③5,4,6,5,7,3;④,3,1,0,0,.其中平均数和中位数相等的一组数据是
A.① B.② C.③ D.①②③④
3.从某企业生产的某种产品中随机抽取10件,测量这些产品的一项质量指标,其频率分布表如下:
质量指标分组 , , ,
频率 0.1 0.6 0.3
则可估计这批产品的质量指标的众数、中位数为
A. B.40,43 C. D.30,43
4.某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.则该物质含量的众数和平均数分别为
A.83和84 B.83和85 C.85和84 D.85和85
5.期中考试以后,班长算出了全班40个人数学成绩的平均分为,如果把当成一个同学的分数,与原来的40个分数一起,算出这41个分数的平均值为,那么为
A. B.1 C. D.2
6.某一个班全体学生参加物理测试,成绩的频率分布直方图如图,则该班的平均分估计是
A.70 B.75 C.68 D.66
7.如图是一组样本数据的频率分布直方图,则依据图形中的数据,可以估计总体的平均数与中位数分别是
A.12.5,12.5 B.13.5,13 C.13.5,12.5 D.13,13
8.已知样本数据,,,,其中,,的平均数为;,,,的平均数为,则样本数据的平均数为
A. B. C. D.
9.下面是甲、乙两位同学高三上学期的5次联考数学成绩,现只知其从第1次到第5次分数所在区间段分布的条形图(从左至右依次为第1至第5次),则从图中可以读出一定正确的信息是
A.甲同学的成绩的平均数大于乙同学的成绩的平均数
B.甲同学的成绩的方差大于乙同学的成绩的方差
C.甲同学的成绩的极差小于乙同学的成绩的极差
D.甲同学的成绩的中位数小于乙同学的成绩的中位数
10.为了解高三学生居家学习时长,从某校的调查问卷中,随机抽取个学生的调查问卷进行分析,得到学生可接受的学习时长频率分布直方图(如图所示),已知学习时长在,的学生人数为25,则的值为
A.70 B.60 C.50 D.40
二.多选题
11.如表为2019年某煤炭公司月份的煤炭生产量,
月份 1 2 3 4 5 6 7 8 9 10
产量(单位:万吨) 23 25 24 17.5 17.5 21 26 29 30 27
则下列结论正确的是
A.极差为12.5万吨 B.平均值为24万吨
C.中位数为24万吨 D.众数为17.5万吨
12.在疫情防护知识竞赛中,对某校的2000名考生的参赛成绩进行统计,可得到如图所示的频率分布直方图,其中分组的区间为,,,,,,,,,,,,60分以下视为不及格,若同一组中数据用该组区间中间值作代表值,则下列说法中正确的是
A.考生竞赛成绩的众数为75分
B.不及格的考生人数为500
C.考生竞赛成绩的平均数为72.5分
D.考生竞赛成绩的中位数为75分
三.填空题
13.某班级有50名同学,一次数学测试平均成绩是92,其中学号为前30名的同学平均成绩为90,则后20名同学的平均成绩为 .
14.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差是 .
15.为了科普“新型冠状病毒”相关知识,增强中学生预防意识,某中学随机抽取30名学生参加相关知识测试,得分(十分制)如图所示,假设得分的中位数为,众数为,平均数为,则,,的大小关系为 .(用“”连接)
16.若有一个企业,的员工收入1万,的员工年收入3万,的员工年收入11万,则该企业员工的年收入的平均数是 万,中位数是 万,众数是 万.
四.解答题
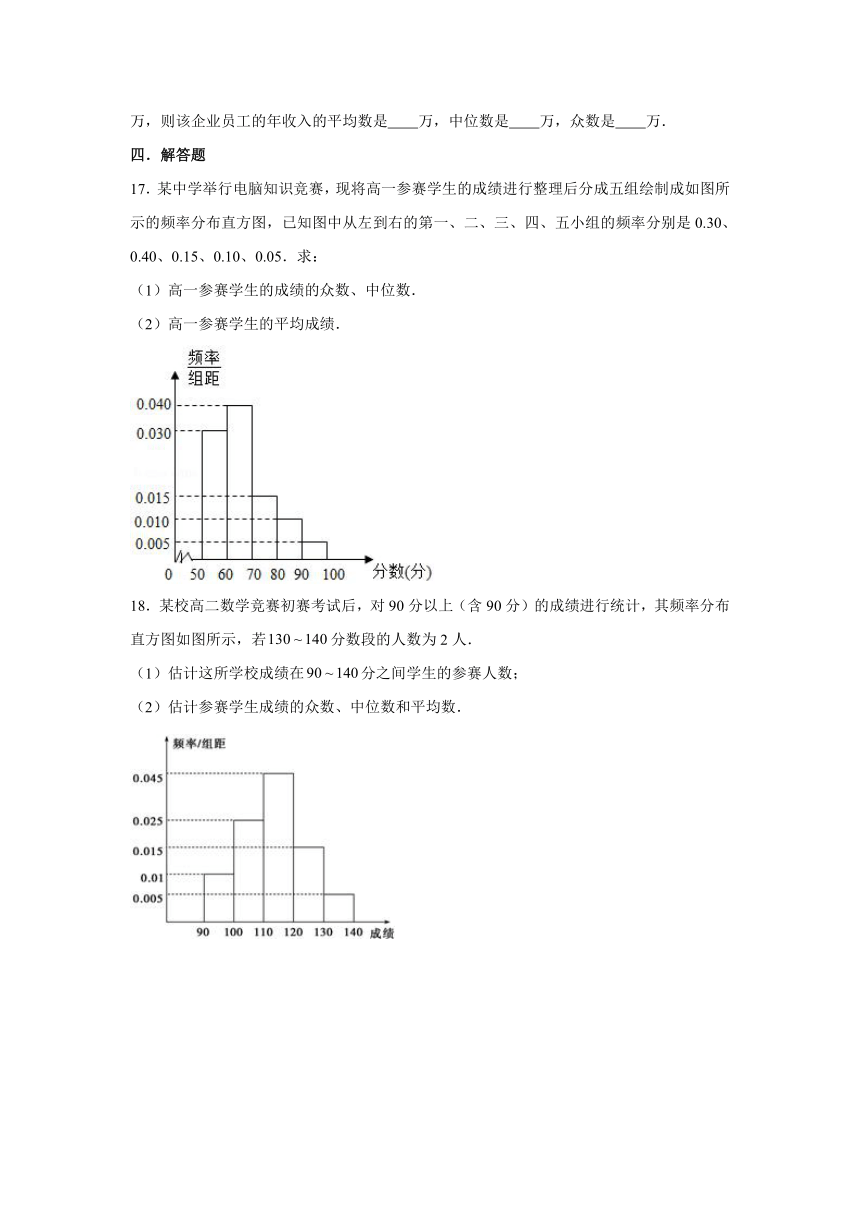
17.某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30、0.40、0.15、0.10、0.05.求:
(1)高一参赛学生的成绩的众数、中位数.
(2)高一参赛学生的平均成绩.
18.某校高二数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,若分数段的人数为2人.
(1)估计这所学校成绩在分之间学生的参赛人数;
(2)估计参赛学生成绩的众数、中位数和平均数.
9.2.3总体集中趋势的估计 同步练习答案
1.解:根据题意,数据为10,30,50,50,60,70,80,
其平均数,
从小到大排列后,最中间的数为50,则中位数为50,
50出现2次,次数最多,则众数为50,
则有众数中位数平均数,
故选:.
2.解:①18,32,,14,8,12;
中位数是,平均数是13
①中两个数相同,
②21,4,7,14,,11;
中位数是9,平均数是9,
②中两个数字相同,
③5,4,6,5,7,3;
中位数是5,平均数是5
两个数字相同,
④,3,1,0,0,.
中位数是0,平均数是0
两个数字相同,
总上可知①②③④都满足条件,
故选:.
3.解:根据频率分布表知,,的频率为0.6,所以众数为,
中位数在,内,可设为,则,解得.
故选:.
4.解:根据频率分布直方图得出众数落在第三组,内,
所以众数为,
含量在,之间的频率为0.1,
含量在,之间的频率为0.2,
含量在,之间的频率为0.4,
根据概率和为1,可得含量在,之间的频率为0.3,
所以频率分布直方图的平均数为:
.
故选:.
5.解:全班40个人数学成绩的平均分为,
把当成一个同学的分数,
则班中有41名同学共为,
人的平均分,
故选:.
6.解:根据频率分布直方图,得:
该班的平均分估计是
;
故选:.
7.解:根据频率分布直方图可以得到第一组的频率为0.2,
第二组的频率为0.5,则第三组的频率为0.3,
则平均数为,
由中位数的概念可以得到中位数在第二组区间,的的位置,
即中位数为.
故选:.
8.解:,,的平均数为;,,的和为,
,,,的平均数为,,,,的和为,
则样本数据的和为,
样本数据的平均数为
故选:.
9.解:对于,甲同学的平均成绩有一个内的数,两个内的数,没有内的数,
他的成绩低于乙同学的平均数,错误;
对于,甲同学的成绩更集中些,他的成绩方差小于乙同学成绩的方差,错误;
对于,由频数分布表知甲的极差可以为,乙的极差可以为,
所以甲的极差也可能大于乙的极差,错误;
对于,甲同学的中位数在,乙同学的中位数在,
所以甲的中位数小于乙的中位数,正确.
故选:.
10.解:由频率分布直方图得学习时长在,的频率为:
,
学习时长在,的学生人数为25,
.
故选:.
11.解:将产量按照从小到大的顺序排列为:17.5,17,5,21,23,24,25,26,27,29,30,
极差为万吨,即正确;
平均值为万吨,即正确;
中位数为,即错误;
众数为17.5万吨,即正确.
故选:.
12.解:对于,由频率分布直方图得考生竞赛成绩的众数为分,故正确;
对于,不及格的考生人数为:,故错误;
对于,考生竞赛成绩的平均数为:
分,故正确;
对于,,的频率为,
,的频率为,
考生竞赛成绩的中位数为:分,故错误.
故选:.
13.解:设学号为31号到50号同学的平均成绩为,
则,解得:,
故答案为:95.
14.解:在输入的过程中错将其中一个数据105输入为15
少输入90,而平均数少3,
求出的平均数减去实际的平均数等于.
故答案为:.
15.解:由条形图知,30名学生的得分为从小到大排列为:
3,3,4,4,4,5,5,5,5,5,5,5,5,5,5,6,6,6,6,6,6,7,7,7,8,8,9,9,10,10;
所以这组数据的中位数为,
众数为,
平均数为,
所以,,的大小关系为.
故答案为:.
16.解:根据题意,得;
该企业员工的年收入的平均数是
万,
又,所以中位数是1万,
且,所以众数是1万.
故答案为:2,1,1.
17.解:(1)用频率分布直方图中最高矩形所在的区间的中点值作为众数的近似值,得众数为65,
又第一个小矩形的面积为0.3,
设第二个小矩形底边的一部分长为,
则,得,
中位数为;
(2)依题意,平均成绩为:
,
平均成绩约为67.
18.解:(1)分数段的人数为2人
又分数段的频率为:
分之间的人数为人
(2),,,,之间的人数依次为:
人,人,人,人,2人
参赛学生成绩的众数的估计值为115分
中位数的估计值为分
平均数的估计值为分
一.单选题
1.已知一组数据为10,30,50,50,60,70,80.其中平均数、中位数和众数的大小关系是
A.平均数中位数众数 B.平均数中位数众数
C.中位数众数平均数 D.众数中位数平均数
2.已知数据①18,32,,14,8,12;②21,4,7,14,,11;③5,4,6,5,7,3;④,3,1,0,0,.其中平均数和中位数相等的一组数据是
A.① B.② C.③ D.①②③④
3.从某企业生产的某种产品中随机抽取10件,测量这些产品的一项质量指标,其频率分布表如下:
质量指标分组 , , ,
频率 0.1 0.6 0.3
则可估计这批产品的质量指标的众数、中位数为
A. B.40,43 C. D.30,43
4.某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.则该物质含量的众数和平均数分别为
A.83和84 B.83和85 C.85和84 D.85和85
5.期中考试以后,班长算出了全班40个人数学成绩的平均分为,如果把当成一个同学的分数,与原来的40个分数一起,算出这41个分数的平均值为,那么为
A. B.1 C. D.2
6.某一个班全体学生参加物理测试,成绩的频率分布直方图如图,则该班的平均分估计是
A.70 B.75 C.68 D.66
7.如图是一组样本数据的频率分布直方图,则依据图形中的数据,可以估计总体的平均数与中位数分别是
A.12.5,12.5 B.13.5,13 C.13.5,12.5 D.13,13
8.已知样本数据,,,,其中,,的平均数为;,,,的平均数为,则样本数据的平均数为
A. B. C. D.
9.下面是甲、乙两位同学高三上学期的5次联考数学成绩,现只知其从第1次到第5次分数所在区间段分布的条形图(从左至右依次为第1至第5次),则从图中可以读出一定正确的信息是
A.甲同学的成绩的平均数大于乙同学的成绩的平均数
B.甲同学的成绩的方差大于乙同学的成绩的方差
C.甲同学的成绩的极差小于乙同学的成绩的极差
D.甲同学的成绩的中位数小于乙同学的成绩的中位数
10.为了解高三学生居家学习时长,从某校的调查问卷中,随机抽取个学生的调查问卷进行分析,得到学生可接受的学习时长频率分布直方图(如图所示),已知学习时长在,的学生人数为25,则的值为
A.70 B.60 C.50 D.40
二.多选题
11.如表为2019年某煤炭公司月份的煤炭生产量,
月份 1 2 3 4 5 6 7 8 9 10
产量(单位:万吨) 23 25 24 17.5 17.5 21 26 29 30 27
则下列结论正确的是
A.极差为12.5万吨 B.平均值为24万吨
C.中位数为24万吨 D.众数为17.5万吨
12.在疫情防护知识竞赛中,对某校的2000名考生的参赛成绩进行统计,可得到如图所示的频率分布直方图,其中分组的区间为,,,,,,,,,,,,60分以下视为不及格,若同一组中数据用该组区间中间值作代表值,则下列说法中正确的是
A.考生竞赛成绩的众数为75分
B.不及格的考生人数为500
C.考生竞赛成绩的平均数为72.5分
D.考生竞赛成绩的中位数为75分
三.填空题
13.某班级有50名同学,一次数学测试平均成绩是92,其中学号为前30名的同学平均成绩为90,则后20名同学的平均成绩为 .
14.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差是 .
15.为了科普“新型冠状病毒”相关知识,增强中学生预防意识,某中学随机抽取30名学生参加相关知识测试,得分(十分制)如图所示,假设得分的中位数为,众数为,平均数为,则,,的大小关系为 .(用“”连接)
16.若有一个企业,的员工收入1万,的员工年收入3万,的员工年收入11万,则该企业员工的年收入的平均数是 万,中位数是 万,众数是 万.
四.解答题
17.某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30、0.40、0.15、0.10、0.05.求:
(1)高一参赛学生的成绩的众数、中位数.
(2)高一参赛学生的平均成绩.
18.某校高二数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,若分数段的人数为2人.
(1)估计这所学校成绩在分之间学生的参赛人数;
(2)估计参赛学生成绩的众数、中位数和平均数.
9.2.3总体集中趋势的估计 同步练习答案
1.解:根据题意,数据为10,30,50,50,60,70,80,
其平均数,
从小到大排列后,最中间的数为50,则中位数为50,
50出现2次,次数最多,则众数为50,
则有众数中位数平均数,
故选:.
2.解:①18,32,,14,8,12;
中位数是,平均数是13
①中两个数相同,
②21,4,7,14,,11;
中位数是9,平均数是9,
②中两个数字相同,
③5,4,6,5,7,3;
中位数是5,平均数是5
两个数字相同,
④,3,1,0,0,.
中位数是0,平均数是0
两个数字相同,
总上可知①②③④都满足条件,
故选:.
3.解:根据频率分布表知,,的频率为0.6,所以众数为,
中位数在,内,可设为,则,解得.
故选:.
4.解:根据频率分布直方图得出众数落在第三组,内,
所以众数为,
含量在,之间的频率为0.1,
含量在,之间的频率为0.2,
含量在,之间的频率为0.4,
根据概率和为1,可得含量在,之间的频率为0.3,
所以频率分布直方图的平均数为:
.
故选:.
5.解:全班40个人数学成绩的平均分为,
把当成一个同学的分数,
则班中有41名同学共为,
人的平均分,
故选:.
6.解:根据频率分布直方图,得:
该班的平均分估计是
;
故选:.
7.解:根据频率分布直方图可以得到第一组的频率为0.2,
第二组的频率为0.5,则第三组的频率为0.3,
则平均数为,
由中位数的概念可以得到中位数在第二组区间,的的位置,
即中位数为.
故选:.
8.解:,,的平均数为;,,的和为,
,,,的平均数为,,,,的和为,
则样本数据的和为,
样本数据的平均数为
故选:.
9.解:对于,甲同学的平均成绩有一个内的数,两个内的数,没有内的数,
他的成绩低于乙同学的平均数,错误;
对于,甲同学的成绩更集中些,他的成绩方差小于乙同学成绩的方差,错误;
对于,由频数分布表知甲的极差可以为,乙的极差可以为,
所以甲的极差也可能大于乙的极差,错误;
对于,甲同学的中位数在,乙同学的中位数在,
所以甲的中位数小于乙的中位数,正确.
故选:.
10.解:由频率分布直方图得学习时长在,的频率为:
,
学习时长在,的学生人数为25,
.
故选:.
11.解:将产量按照从小到大的顺序排列为:17.5,17,5,21,23,24,25,26,27,29,30,
极差为万吨,即正确;
平均值为万吨,即正确;
中位数为,即错误;
众数为17.5万吨,即正确.
故选:.
12.解:对于,由频率分布直方图得考生竞赛成绩的众数为分,故正确;
对于,不及格的考生人数为:,故错误;
对于,考生竞赛成绩的平均数为:
分,故正确;
对于,,的频率为,
,的频率为,
考生竞赛成绩的中位数为:分,故错误.
故选:.
13.解:设学号为31号到50号同学的平均成绩为,
则,解得:,
故答案为:95.
14.解:在输入的过程中错将其中一个数据105输入为15
少输入90,而平均数少3,
求出的平均数减去实际的平均数等于.
故答案为:.
15.解:由条形图知,30名学生的得分为从小到大排列为:
3,3,4,4,4,5,5,5,5,5,5,5,5,5,5,6,6,6,6,6,6,7,7,7,8,8,9,9,10,10;
所以这组数据的中位数为,
众数为,
平均数为,
所以,,的大小关系为.
故答案为:.
16.解:根据题意,得;
该企业员工的年收入的平均数是
万,
又,所以中位数是1万,
且,所以众数是1万.
故答案为:2,1,1.
17.解:(1)用频率分布直方图中最高矩形所在的区间的中点值作为众数的近似值,得众数为65,
又第一个小矩形的面积为0.3,
设第二个小矩形底边的一部分长为,
则,得,
中位数为;
(2)依题意,平均成绩为:
,
平均成绩约为67.
18.解:(1)分数段的人数为2人
又分数段的频率为:
分之间的人数为人
(2),,,,之间的人数依次为:
人,人,人,人,2人
参赛学生成绩的众数的估计值为115分
中位数的估计值为分
平均数的估计值为分
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
