9.2.4总体离散程度的估计-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习Word含解析
文档属性
| 名称 | 9.2.4总体离散程度的估计-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习Word含解析 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 00:00:00 | ||
图片预览




文档简介
9.2.4总体离散程度的估计 同步练习
一.单选题
1.已知样本数据3,2,1,的平均数为2,则样本的标准差是
A. B. C. D.
2.一组数据的平均数为,方差为,将这组数据的每个数都乘以得到一组新数据,则下列说法正确的是
A.这组新数据的平均数为 B.这组新数据的平均数为
C.这组新数据的方差为 D.这组新数据的标准差为
3.有专业机构认为某流感在一段时间没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过15人”.根据过去10天甲、乙、丙、丁四地新增死疑似病例数据,一定符合该标志的是
A.甲地:总体均值为4,中位数为3
B.乙地:总体均值为5,总体方差为12
C.丙地:中位数为3,众数为2
D.丁地:总体均值为3,总体方差大于0
4.设一组样本数据,,,的方差为100,数据,,,的方差为
A.0.1 B.1 C.10 D.100
5.学校组织开展劳动实践,高二某班15名学生利用假期时间前往敬老院、消防队等场所劳动服务.经统计,该15名学生的劳动服务时长平均为20小时,标准差为.后来经核实,发现统计的甲、乙两名同学的劳动服务时长有误.甲同学的劳动服务时长实际为20小时,被误统计为15小时;乙同学的劳动服务时长实际为18小时,被误统计为23小时.更正后重新计算,得到标准差为,则与的大小关系为
A. B. C. D.无法判断
6.一组数据由10个数组成,将其中一个数由4改为1,另一个数由6改为9,其余数不变,得到新的10个数,则新的一组数的方差相比原先一组数的方差的增加值为
A.2 B.3 C.4 D.5
7.气象意义上从春季进入夏季的标志为“连续5天的每日平均温度不低于”,现有甲、乙、丙三地连续5天的每日平均温度的记录数据(记录的数据都是正整数,单位为
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体均值为24;
③丙地:5个数据中有1个数据是32,总体均值为26,总方差为10.8.
其中肯定进入夏季的地区有
A.①② B.①③ C.②③ D.①②③
8.是评估空气质量的一个重要指标,我国标准采用世卫组织设定的最宽限值,即月均值在以下空气质量为一级,在之间空气质量为二级,在以上空气质量为超标.某地区2020年1月至12月的月均值(单位:的统计数据如图所示,则下列叙述不正确的是
A.该地区一年中空气质量超标的月份只有1个月
B.该地区一年中月均值2月到7月的方差比8月到11月的方差大
C.该地区上半年中月均值的平均数约为61.83
D.该地区从2月份到7月份值持续增加
二.多选题
9.一组数据按从小到大排列为2,3,3,,7,10,若这组数据的平均数是中位数的倍,则下列说法正确的是
A. B.众数为3 C.中位数为4 D.方差为
10.为促进儿童全面发展和健康成长,我国于2011年颁布实施《中国儿童发展纲要年)》.儿童文化产品和活动场所更加丰富.近年来,儿童接触文化艺术和娱乐体验的途径更加多元,可获得的文化产品和服务也更加丰富.如图为年少儿广播节目、少儿电视节目、电视动画节目播出时间.则下列结论中正确的是
A.2018年全国少儿电视节目播出时间比上一年增长
B.年少儿广播节目播出时间的平均数约为21万小时
C.年少儿广播节目、少儿电视节目、电视动画节目播出时间均逐年增长
D.年少儿广播节目、少儿电视节目、电视动画节目播出时间中电视动画节目播出时间的方差最小
11.给出如下数据:
第一组:3,11,5,13,7,2,6,8,9.
第二组:12,20,14,22,16,11,15,17,18.
则这两组数据的
A.平均数相等 B.中位数相等 C.极差相等 D.方差相等
12.在第一次全市高三年级统考后,某数学老师为了解本班学生的本次数学考试情况,将全班50名学生的数学成绩绘制成频率分布直方图.已知该班级学生的数学成绩全部介于65分到145分之间(满分150分),将数学成绩按如下方式分成八组:第一组,,第二组,,,第八组,,按上述分组方法得到的频率分布直方图的一部分,如图所示,则下列结论正确的是
A.第七组的频率为0.008
B.该班级数学成绩的中位数的估计值为101分
C.该班级数学成绩的平均分的估计值大于95分
D.该班级数学成绩的方差的估计值大于26
三.填空题
13.已知一组数据,3,,6的中位数为4,则其总体方差为 .
14.某医院急救中心随机抽取20位病人等待急诊的时间记录如表:
等待时间分 , , , , ,
频数 4 8 5 2 1
用上述分组资料计算出病人平均等待时间的估计值 ,病人等待时间方差的估计值 .
15.若,,,这20个数据的平均数为,方差为0.21,则,,,,这21个数据的方差为 .
16.某班48名同学,在一次考试中统计出平均分为70,方差为75,后来发现有2名同学的分数登记错了,甲实际得了80分,却记成了50分,乙实际得了70分,却记成了100分,更正后方差应为 .
四.解答题
17.从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 , , , , ,
频数 6 26 38 22 8
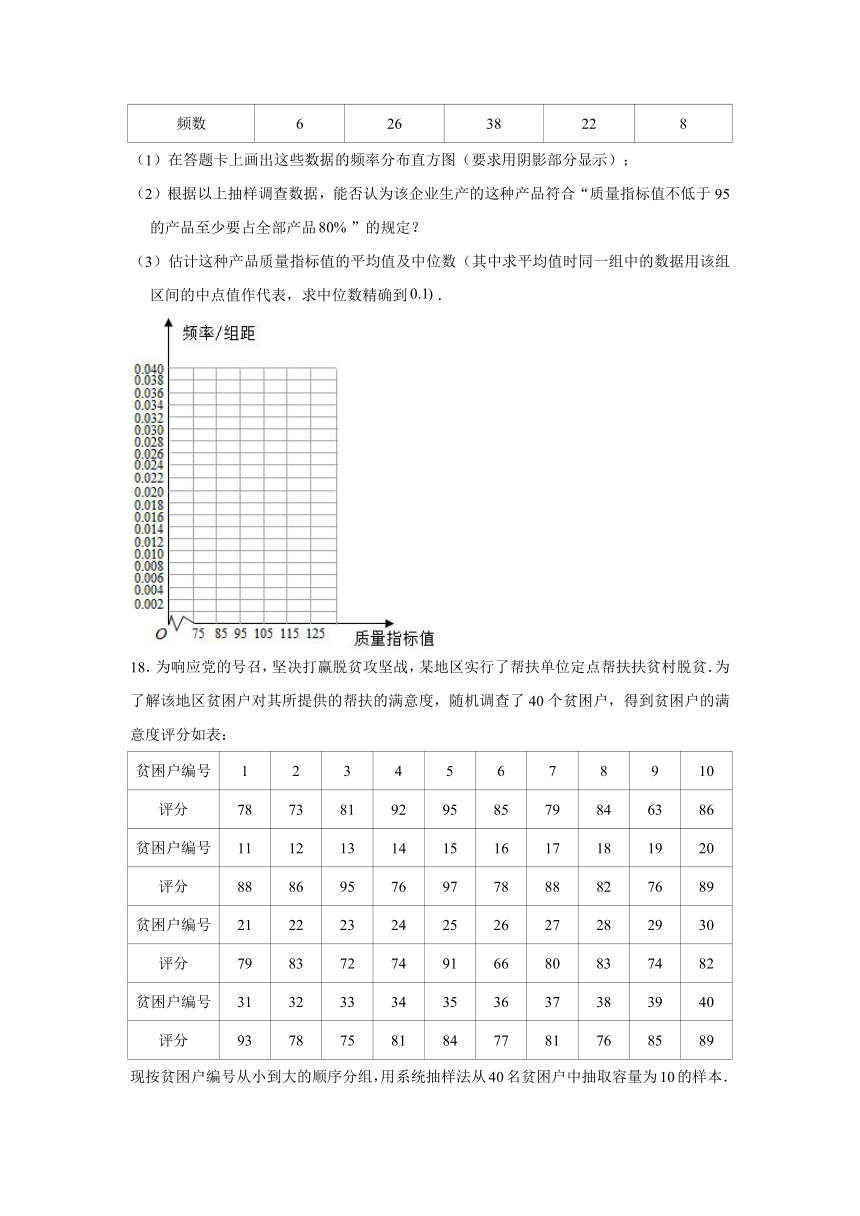
(1)在答题卡上画出这些数据的频率分布直方图(要求用阴影部分显示);
(2)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品”的规定?
(3)估计这种产品质量指标值的平均值及中位数(其中求平均值时同一组中的数据用该组区间的中点值作代表,求中位数精确到.
18.为响应党的号召,坚决打赢脱贫攻坚战,某地区实行了帮扶单位定点帮扶扶贫村脱贫.为了解该地区贫困户对其所提供的帮扶的满意度,随机调查了40个贫困户,得到贫困户的满意度评分如表:
贫困户编号 1 2 3 4 5 6 7 8 9 10
评分 78 73 81 92 95 85 79 84 63 86
贫困户编号 11 12 13 14 15 16 17 18 19 20
评分 88 86 95 76 97 78 88 82 76 89
贫困户编号 21 22 23 24 25 26 27 28 29 30
评分 79 83 72 74 91 66 80 83 74 82
贫困户编号 31 32 33 34 35 36 37 38 39 40
评分 93 78 75 81 84 77 81 76 85 89
现按贫困户编号从小到大的顺序分组,用系统抽样法从40名贫困户中抽取容量为10的样本.
(Ⅰ)若在第一分段里随机抽到的第一个样本的评分数据为81,记第二和第十个样本的评分数据分别为,,请写出,的值;
(Ⅱ)若10个样本的评分数据分别为92,84,86,78,89,74,83,78,77,89.请你计算所抽到的10个样本的平均数和方差;
9.2.4总体离散程度的估计 同步练习答案
1.解:样本数据3,2,1,的平均数为,,
样本的方差,标准差为,
故选:.
2.解:根据题意,一组数据的平均数为,方差为,将这组数据的每个数都乘以得到一组新数据,
则新数据的平均数为,方差为,
则其标准差为,
故选:.
3.解:对于,均值为4,中位数为3,不能保证10个数据中每个数据都不超过15,
不符合该标志;
对于,均值为5,方差为12时,假设有一个数据为16,其余数据均相等,
则,
假设不成立,即所有数据不超过15,符合该标志;
同理,对于、,都不能保证10个数据中每个数据不超过15,
、也不符合题意.
故选:.
4.解:数据,,,的方差为100,数据,,,的方差为:.
故选:.
5.解:由已知可得,两次统计的总人数没有变,故两次统计的平均数的相同的,设为,
设劳动时间长为,
则,
,
要比较与的大小,只需比较与的大小即可,
因为,
,
所以,
故.
故选:.
6.解:一个数由4改为1,另一个数由6改为9,故该数据的平均数不变,
设没有改变的八个数分别为,,,,,,,,
原先一组数的方差,
新数据的方差,
所以
,
所以新的一组数的方差相比原先一组数的方差的增加值为3.
故选:.
7.解:对于①,甲地:5个数据的中位数为24,众数为22,
则甲地连续5天的日平均温度的记录数据可能为:22,22,24,25,26,
其连续5天的日平均温度不低于;
对于②,乙地:5个数据的中位数为27,总体均值为24,
当5个数据为19,20,27,27,27时,其连续5天的日平均温度有低于22,故不确定;
对于③,丙地:5个数据中有1个数据是32,总体均值为26,总方差为10.8,
所以其余四天与26差值的平方和为,
若有一天温度低于22度,因为平均值为26,则必有一天高于30度,
所以有,
故可知其连续5天的日平均温度均不低于22.
综上所述,肯定进入夏季的地区有甲、丙两地.
故选:.
8.解:对于,该地区一年中空气质量超标的月份只有6月份这1个月,选项正确;
对于,该地区2月到7月的数据为55,45,56,65,68,82,53,
8月到11月的数据为46,42,36,2月到7月的数据波动性大些,所以方差大,选项正确;
对于,计算月份的月均值为,选项正确;
对于,该地区从2月份到6月份值持续增加,7月份减少,所以选项错误.
故选:.
9.解:一组数据按从小到大排列为2,3,3,,7,10,
这组数据的平均数是中位数的倍,
,
解得,故错误;
众数为3,故正确;
中位数为,故正确;
平均数为:,
方差为:,故正确.
故选:.
10.解:2018年全国少年电视节目播出时间比上一年增长,故错误,
少儿广播节目播出时间的平均数约为21万小时,故正确,
2014年到2015年少儿电视节目播出时间降低,故错误,
由图可知电视动画节目播出时间的方差最小,故正确,
故选:.
11.解:对于,第一组数据的平均数为,
第二组数据的平均数为,所以两组数据的平均数不相等,故选项错误;
对于,第一组数据的中位数是7,第二组数据的中位数是16,所以两组数据的中位数不相等,故选项错误;
对于,第一组数据的极差为,第二组数据的极差为,所以两组数据的极差相等,故选项正确;
对于,第一组数据的方差为
,
第二组数据的方差为
,
所以两组数据的方差相等.
故选:.
12.解:对于,利用频率之和为1,
可得第七组的频率为,故选项错误;
对于,成绩在第一组到第八组的人数分别为2,6,8,15,10,3,4,2,
所以中位数在第四组,内,设中位数为,
则有,
所以,解得,
所以该班级数学成绩的中位数的估计值为101分,故选项正确;
对于,该班级数学成绩的平均分的估计值为:
,故选项正确;
对于,该班级数学成绩的方差的估计值为:
,故选项正确.
故选:.
13.解:因为数据,3,,6的中位数为4,
所以,故,
所以这组数据的平均数为,
故方差为.
故答案为:.
14.解:根据题意计算平均数为;
,
故答案为:9.5,28.5.
15.解:,,,这20个数据的平均数为,方差为0.21,
则,,,,这21个数据的方差为:
.
故答案是:0.20.
16.解:设更正前甲,乙,丙的成绩依次为,,,,
则,即,
,即,
更正后平均分,
方差
.
故答案为:50.
17.解:(1)由已知作出频率分布表为:
质量指标值分组 , , , , ,
频数 6 26 38 22 8
频率 0.06 0.26 0.38 0.22 0.08
由频率分布表作出这些数据的频率分布直方图为:
(2)质量指标值不低于95 的产品所占比例的估计值为.
由于该估计值小于0.8,
故不能认为该企业生产的这种产品“质量指标值不低于95 的产品至少要占全部产品的规定.
(3)质量指标值的样本平均数为:.
,内频率为:,
中位数位于,内,
设中位数为,则,
中位数为99.7.
18.解:(1),.
(2),
一.单选题
1.已知样本数据3,2,1,的平均数为2,则样本的标准差是
A. B. C. D.
2.一组数据的平均数为,方差为,将这组数据的每个数都乘以得到一组新数据,则下列说法正确的是
A.这组新数据的平均数为 B.这组新数据的平均数为
C.这组新数据的方差为 D.这组新数据的标准差为
3.有专业机构认为某流感在一段时间没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过15人”.根据过去10天甲、乙、丙、丁四地新增死疑似病例数据,一定符合该标志的是
A.甲地:总体均值为4,中位数为3
B.乙地:总体均值为5,总体方差为12
C.丙地:中位数为3,众数为2
D.丁地:总体均值为3,总体方差大于0
4.设一组样本数据,,,的方差为100,数据,,,的方差为
A.0.1 B.1 C.10 D.100
5.学校组织开展劳动实践,高二某班15名学生利用假期时间前往敬老院、消防队等场所劳动服务.经统计,该15名学生的劳动服务时长平均为20小时,标准差为.后来经核实,发现统计的甲、乙两名同学的劳动服务时长有误.甲同学的劳动服务时长实际为20小时,被误统计为15小时;乙同学的劳动服务时长实际为18小时,被误统计为23小时.更正后重新计算,得到标准差为,则与的大小关系为
A. B. C. D.无法判断
6.一组数据由10个数组成,将其中一个数由4改为1,另一个数由6改为9,其余数不变,得到新的10个数,则新的一组数的方差相比原先一组数的方差的增加值为
A.2 B.3 C.4 D.5
7.气象意义上从春季进入夏季的标志为“连续5天的每日平均温度不低于”,现有甲、乙、丙三地连续5天的每日平均温度的记录数据(记录的数据都是正整数,单位为
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体均值为24;
③丙地:5个数据中有1个数据是32,总体均值为26,总方差为10.8.
其中肯定进入夏季的地区有
A.①② B.①③ C.②③ D.①②③
8.是评估空气质量的一个重要指标,我国标准采用世卫组织设定的最宽限值,即月均值在以下空气质量为一级,在之间空气质量为二级,在以上空气质量为超标.某地区2020年1月至12月的月均值(单位:的统计数据如图所示,则下列叙述不正确的是
A.该地区一年中空气质量超标的月份只有1个月
B.该地区一年中月均值2月到7月的方差比8月到11月的方差大
C.该地区上半年中月均值的平均数约为61.83
D.该地区从2月份到7月份值持续增加
二.多选题
9.一组数据按从小到大排列为2,3,3,,7,10,若这组数据的平均数是中位数的倍,则下列说法正确的是
A. B.众数为3 C.中位数为4 D.方差为
10.为促进儿童全面发展和健康成长,我国于2011年颁布实施《中国儿童发展纲要年)》.儿童文化产品和活动场所更加丰富.近年来,儿童接触文化艺术和娱乐体验的途径更加多元,可获得的文化产品和服务也更加丰富.如图为年少儿广播节目、少儿电视节目、电视动画节目播出时间.则下列结论中正确的是
A.2018年全国少儿电视节目播出时间比上一年增长
B.年少儿广播节目播出时间的平均数约为21万小时
C.年少儿广播节目、少儿电视节目、电视动画节目播出时间均逐年增长
D.年少儿广播节目、少儿电视节目、电视动画节目播出时间中电视动画节目播出时间的方差最小
11.给出如下数据:
第一组:3,11,5,13,7,2,6,8,9.
第二组:12,20,14,22,16,11,15,17,18.
则这两组数据的
A.平均数相等 B.中位数相等 C.极差相等 D.方差相等
12.在第一次全市高三年级统考后,某数学老师为了解本班学生的本次数学考试情况,将全班50名学生的数学成绩绘制成频率分布直方图.已知该班级学生的数学成绩全部介于65分到145分之间(满分150分),将数学成绩按如下方式分成八组:第一组,,第二组,,,第八组,,按上述分组方法得到的频率分布直方图的一部分,如图所示,则下列结论正确的是
A.第七组的频率为0.008
B.该班级数学成绩的中位数的估计值为101分
C.该班级数学成绩的平均分的估计值大于95分
D.该班级数学成绩的方差的估计值大于26
三.填空题
13.已知一组数据,3,,6的中位数为4,则其总体方差为 .
14.某医院急救中心随机抽取20位病人等待急诊的时间记录如表:
等待时间分 , , , , ,
频数 4 8 5 2 1
用上述分组资料计算出病人平均等待时间的估计值 ,病人等待时间方差的估计值 .
15.若,,,这20个数据的平均数为,方差为0.21,则,,,,这21个数据的方差为 .
16.某班48名同学,在一次考试中统计出平均分为70,方差为75,后来发现有2名同学的分数登记错了,甲实际得了80分,却记成了50分,乙实际得了70分,却记成了100分,更正后方差应为 .
四.解答题
17.从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 , , , , ,
频数 6 26 38 22 8
(1)在答题卡上画出这些数据的频率分布直方图(要求用阴影部分显示);
(2)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品”的规定?
(3)估计这种产品质量指标值的平均值及中位数(其中求平均值时同一组中的数据用该组区间的中点值作代表,求中位数精确到.
18.为响应党的号召,坚决打赢脱贫攻坚战,某地区实行了帮扶单位定点帮扶扶贫村脱贫.为了解该地区贫困户对其所提供的帮扶的满意度,随机调查了40个贫困户,得到贫困户的满意度评分如表:
贫困户编号 1 2 3 4 5 6 7 8 9 10
评分 78 73 81 92 95 85 79 84 63 86
贫困户编号 11 12 13 14 15 16 17 18 19 20
评分 88 86 95 76 97 78 88 82 76 89
贫困户编号 21 22 23 24 25 26 27 28 29 30
评分 79 83 72 74 91 66 80 83 74 82
贫困户编号 31 32 33 34 35 36 37 38 39 40
评分 93 78 75 81 84 77 81 76 85 89
现按贫困户编号从小到大的顺序分组,用系统抽样法从40名贫困户中抽取容量为10的样本.
(Ⅰ)若在第一分段里随机抽到的第一个样本的评分数据为81,记第二和第十个样本的评分数据分别为,,请写出,的值;
(Ⅱ)若10个样本的评分数据分别为92,84,86,78,89,74,83,78,77,89.请你计算所抽到的10个样本的平均数和方差;
9.2.4总体离散程度的估计 同步练习答案
1.解:样本数据3,2,1,的平均数为,,
样本的方差,标准差为,
故选:.
2.解:根据题意,一组数据的平均数为,方差为,将这组数据的每个数都乘以得到一组新数据,
则新数据的平均数为,方差为,
则其标准差为,
故选:.
3.解:对于,均值为4,中位数为3,不能保证10个数据中每个数据都不超过15,
不符合该标志;
对于,均值为5,方差为12时,假设有一个数据为16,其余数据均相等,
则,
假设不成立,即所有数据不超过15,符合该标志;
同理,对于、,都不能保证10个数据中每个数据不超过15,
、也不符合题意.
故选:.
4.解:数据,,,的方差为100,数据,,,的方差为:.
故选:.
5.解:由已知可得,两次统计的总人数没有变,故两次统计的平均数的相同的,设为,
设劳动时间长为,
则,
,
要比较与的大小,只需比较与的大小即可,
因为,
,
所以,
故.
故选:.
6.解:一个数由4改为1,另一个数由6改为9,故该数据的平均数不变,
设没有改变的八个数分别为,,,,,,,,
原先一组数的方差,
新数据的方差,
所以
,
所以新的一组数的方差相比原先一组数的方差的增加值为3.
故选:.
7.解:对于①,甲地:5个数据的中位数为24,众数为22,
则甲地连续5天的日平均温度的记录数据可能为:22,22,24,25,26,
其连续5天的日平均温度不低于;
对于②,乙地:5个数据的中位数为27,总体均值为24,
当5个数据为19,20,27,27,27时,其连续5天的日平均温度有低于22,故不确定;
对于③,丙地:5个数据中有1个数据是32,总体均值为26,总方差为10.8,
所以其余四天与26差值的平方和为,
若有一天温度低于22度,因为平均值为26,则必有一天高于30度,
所以有,
故可知其连续5天的日平均温度均不低于22.
综上所述,肯定进入夏季的地区有甲、丙两地.
故选:.
8.解:对于,该地区一年中空气质量超标的月份只有6月份这1个月,选项正确;
对于,该地区2月到7月的数据为55,45,56,65,68,82,53,
8月到11月的数据为46,42,36,2月到7月的数据波动性大些,所以方差大,选项正确;
对于,计算月份的月均值为,选项正确;
对于,该地区从2月份到6月份值持续增加,7月份减少,所以选项错误.
故选:.
9.解:一组数据按从小到大排列为2,3,3,,7,10,
这组数据的平均数是中位数的倍,
,
解得,故错误;
众数为3,故正确;
中位数为,故正确;
平均数为:,
方差为:,故正确.
故选:.
10.解:2018年全国少年电视节目播出时间比上一年增长,故错误,
少儿广播节目播出时间的平均数约为21万小时,故正确,
2014年到2015年少儿电视节目播出时间降低,故错误,
由图可知电视动画节目播出时间的方差最小,故正确,
故选:.
11.解:对于,第一组数据的平均数为,
第二组数据的平均数为,所以两组数据的平均数不相等,故选项错误;
对于,第一组数据的中位数是7,第二组数据的中位数是16,所以两组数据的中位数不相等,故选项错误;
对于,第一组数据的极差为,第二组数据的极差为,所以两组数据的极差相等,故选项正确;
对于,第一组数据的方差为
,
第二组数据的方差为
,
所以两组数据的方差相等.
故选:.
12.解:对于,利用频率之和为1,
可得第七组的频率为,故选项错误;
对于,成绩在第一组到第八组的人数分别为2,6,8,15,10,3,4,2,
所以中位数在第四组,内,设中位数为,
则有,
所以,解得,
所以该班级数学成绩的中位数的估计值为101分,故选项正确;
对于,该班级数学成绩的平均分的估计值为:
,故选项正确;
对于,该班级数学成绩的方差的估计值为:
,故选项正确.
故选:.
13.解:因为数据,3,,6的中位数为4,
所以,故,
所以这组数据的平均数为,
故方差为.
故答案为:.
14.解:根据题意计算平均数为;
,
故答案为:9.5,28.5.
15.解:,,,这20个数据的平均数为,方差为0.21,
则,,,,这21个数据的方差为:
.
故答案是:0.20.
16.解:设更正前甲,乙,丙的成绩依次为,,,,
则,即,
,即,
更正后平均分,
方差
.
故答案为:50.
17.解:(1)由已知作出频率分布表为:
质量指标值分组 , , , , ,
频数 6 26 38 22 8
频率 0.06 0.26 0.38 0.22 0.08
由频率分布表作出这些数据的频率分布直方图为:
(2)质量指标值不低于95 的产品所占比例的估计值为.
由于该估计值小于0.8,
故不能认为该企业生产的这种产品“质量指标值不低于95 的产品至少要占全部产品的规定.
(3)质量指标值的样本平均数为:.
,内频率为:,
中位数位于,内,
设中位数为,则,
中位数为99.7.
18.解:(1),.
(2),
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
