1.3.1 柱体、锥体、台体的表面积与体积课件(共28张PPT)2020-2021学年高一数学人教A版必修2第一章
文档属性
| 名称 | 1.3.1 柱体、锥体、台体的表面积与体积课件(共28张PPT)2020-2021学年高一数学人教A版必修2第一章 |  | |
| 格式 | ppt | ||
| 文件大小 | 881.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 17:43:44 | ||
图片预览



文档简介
(共28张PPT)
柱体、锥体、台体的表面积
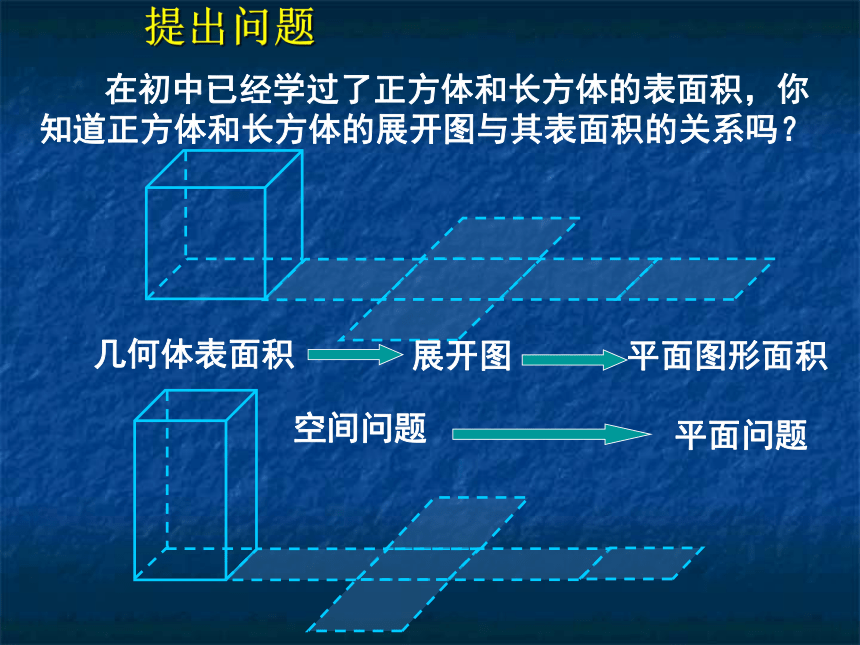
在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?
几何体表面积
展开图
平面图形面积
空间问题
平面问题
提出问题
正方体、长方体是由多个平面围成的几何体,它们的表面积就是各个面的面积的和.
因此,我们可以把它们展成平面图形,利用平面图形求面积的方法,求立体图形的表面积.
引入新课
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?
探究
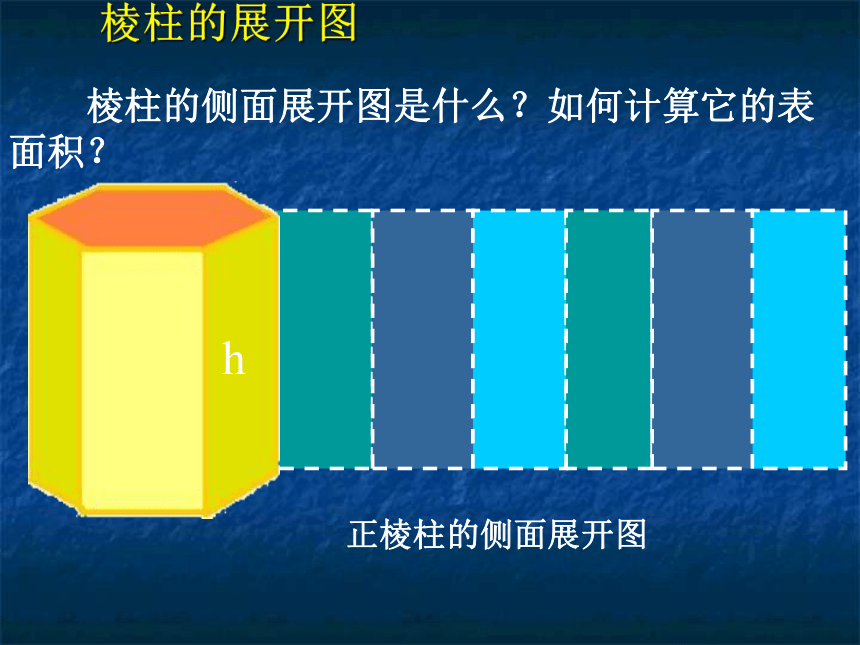
棱柱的侧面展开图是什么?如何计算它的表面积?
h
棱柱的展开图
正棱柱的侧面展开图
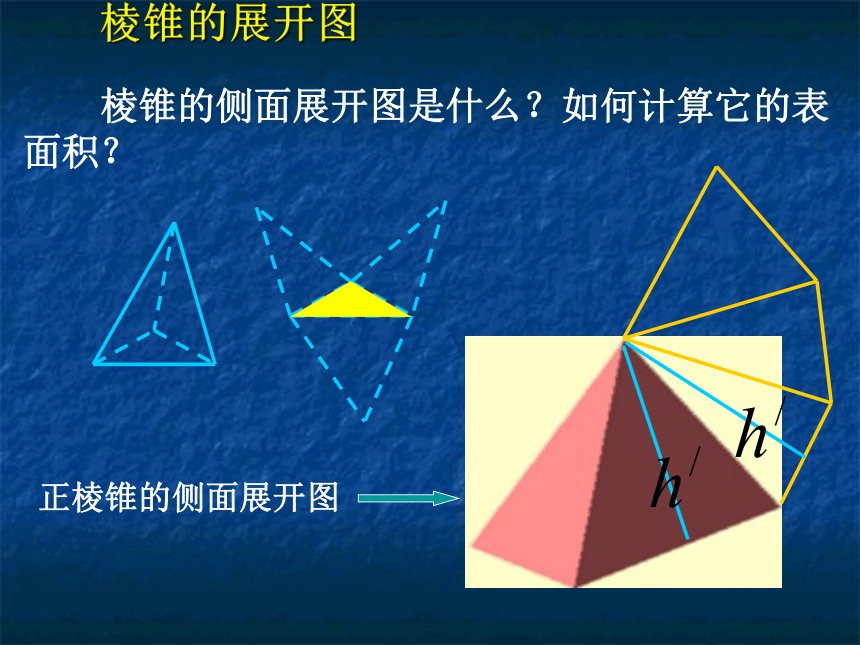
棱锥的侧面展开图是什么?如何计算它的表面积?
棱锥的展开图
正棱锥的侧面展开图
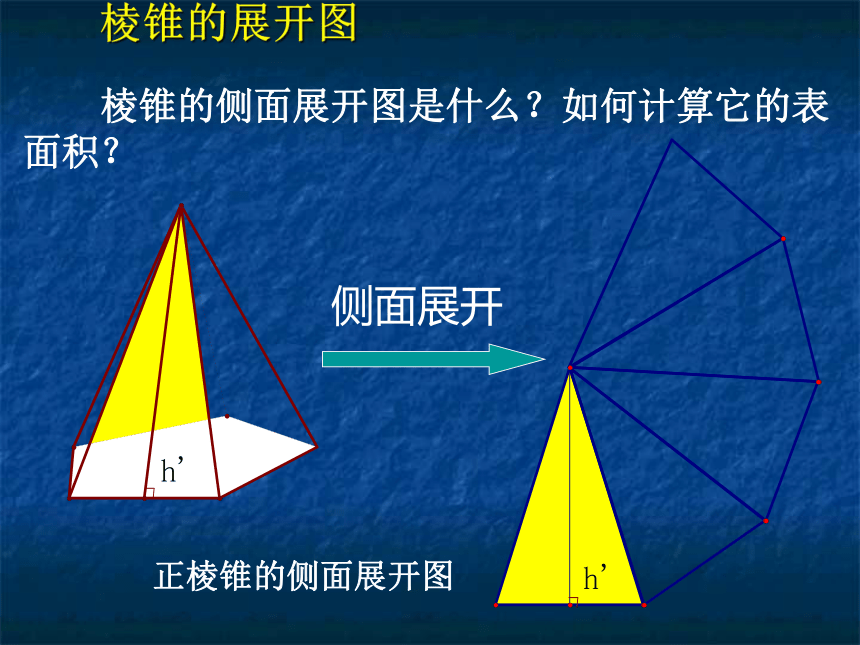
棱锥的侧面展开图是什么?如何计算它的表面积?
棱锥的展开图
侧面展开
正棱锥的侧面展开图
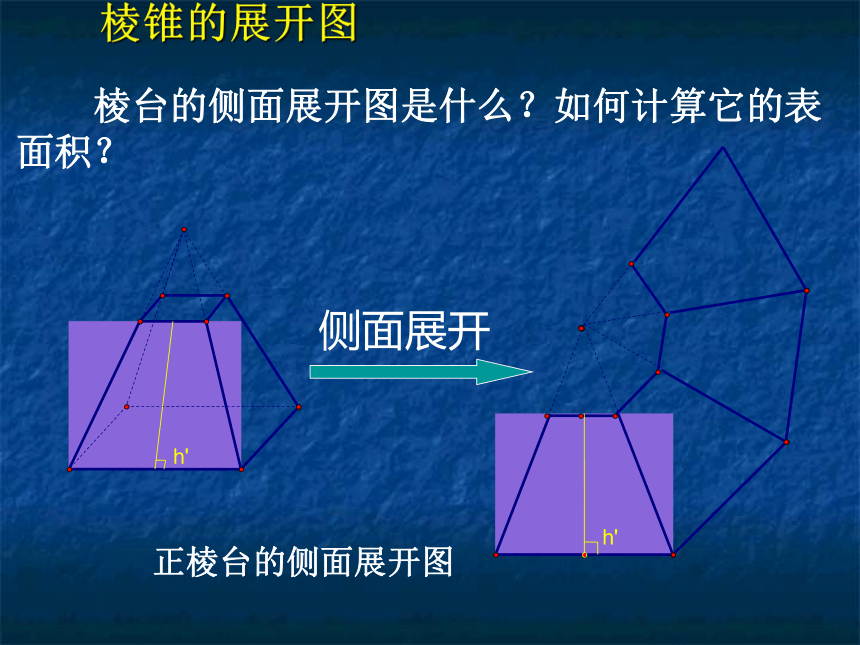
棱台的侧面展开图是什么?如何计算它的表面积?
棱锥的展开图
侧面展开
h'
h'
正棱台的侧面展开图
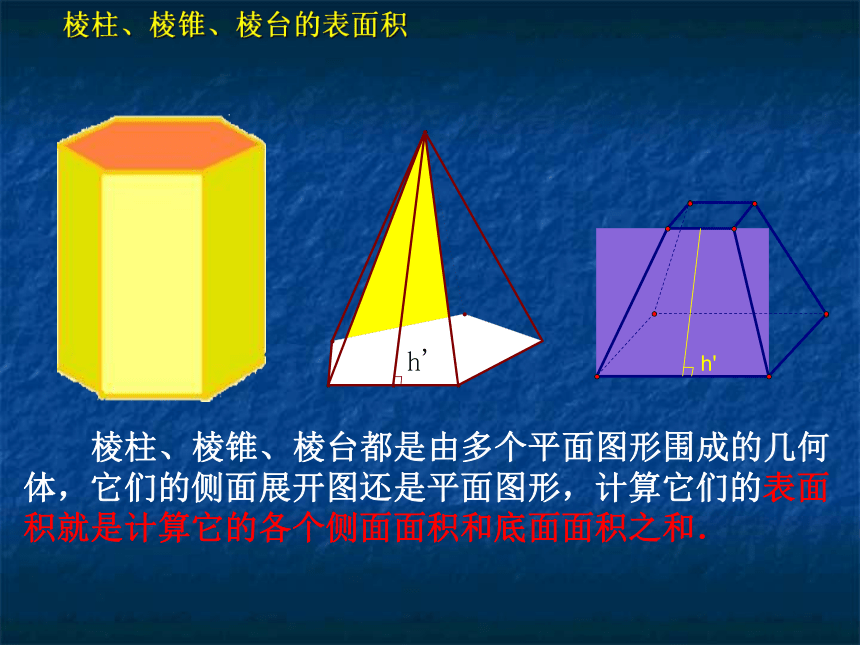
棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧面展开图还是平面图形,计算它们的表面积就是计算它的各个侧面面积和底面面积之和.
h'
例1
已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积
.
D
B
C
A
S
分析:四面体的展开图是由四个全等的正三角形组成.
因为BC=a,
所以:
因此,四面体S-ABC
的表面积.
交BC于点D.
解:先求
的面积,过点S作
,
典型例题
求多面体的表面积可以通过求各个平面多边形的面积和得到,那么旋转体的面积该如何求呢?
思考
圆柱的表面积
O
圆柱的侧面展开图是矩形
圆锥的表面积
圆锥的侧面展开图是扇形
O
圆台的表面积
参照圆柱和圆锥的侧面展开图,试想象圆台的侧面展开图是什么
.
O
O’
圆台的侧面展开图是扇环
三者之间关系
O
O’
O
O
圆柱、圆锥、圆台三者的表面积公式之间有什么关系?
r’=r
上底扩大
r’=0
上底缩小
例2
如图,一个圆台形花盆盆口直径20
cm,盆底直径为15cm,底部渗水圆孔直径为1.5
cm,盆壁长15cm.那么花盆的表面积约是多少平方厘米(
取3.14,结果精确到1
)?
解:由圆台的表面积公式得
花盆的表面积:
答:花盆的表面积约是999
.
典型例题
课堂练习
1、一个三棱柱的底面是正三角形,边长为4,侧棱与底面垂直,侧棱长10,求其表面积.
2、一个圆台,上、下底面半径分别为10、20,母线与底面的夹角为60°,求圆台的表面积.
变式:求切割之前的圆锥的表面积
3、面积为2的菱形,绕其一边旋转一周所得几何体的表面积是多少?
4、若一个圆锥的轴截面是等边三角形,其面积为3,求这个圆锥的表面积
柱体、锥体、台体的体积
1、长方体的体积
D
A
B
C
D1
A1
B1
C1
等底等高柱体的体积相等吗?
2、柱体的体积
定理:等底等高柱体的体积相等
祖恒原理
将一个三棱柱按如图所示分解成三个三棱锥,那么这三个三棱锥的体积有什么关系?它们与三棱柱的体积有什么关系?
1
2
3
1
2
3
思考4:推广到一般的棱锥和圆锥,你猜想锥体的体积公式是什么?
高h
底面积S
3、锥体的体积
定理:等底等高锥体的体积相等
等底等高的棱柱和棱锥体积的关系
4、台体的体积
例3
有一堆规格相同的铁制六角螺帽共重5.8kg(铁的密度是7.8g/cm3),已知螺帽的底面是正六边形,边长为12mm,内孔直径为10mm,,高为10mm,问这堆螺帽大约有多少个?
求此棱柱挖去圆柱后的体积和表面积
引申:1.圆柱的侧面展开图如下左图所示,求此圆柱的体积。
侧面展开图
直观图1
直观图2
引申2:已知正四棱台两底面的边长,
和棱台体积,
求棱台的高.
柱体、锥体、台体的表面积
在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?
几何体表面积
展开图
平面图形面积
空间问题
平面问题
提出问题
正方体、长方体是由多个平面围成的几何体,它们的表面积就是各个面的面积的和.
因此,我们可以把它们展成平面图形,利用平面图形求面积的方法,求立体图形的表面积.
引入新课
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?
探究
棱柱的侧面展开图是什么?如何计算它的表面积?
h
棱柱的展开图
正棱柱的侧面展开图
棱锥的侧面展开图是什么?如何计算它的表面积?
棱锥的展开图
正棱锥的侧面展开图
棱锥的侧面展开图是什么?如何计算它的表面积?
棱锥的展开图
侧面展开
正棱锥的侧面展开图
棱台的侧面展开图是什么?如何计算它的表面积?
棱锥的展开图
侧面展开
h'
h'
正棱台的侧面展开图
棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧面展开图还是平面图形,计算它们的表面积就是计算它的各个侧面面积和底面面积之和.
h'
例1
已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积
.
D
B
C
A
S
分析:四面体的展开图是由四个全等的正三角形组成.
因为BC=a,
所以:
因此,四面体S-ABC
的表面积.
交BC于点D.
解:先求
的面积,过点S作
,
典型例题
求多面体的表面积可以通过求各个平面多边形的面积和得到,那么旋转体的面积该如何求呢?
思考
圆柱的表面积
O
圆柱的侧面展开图是矩形
圆锥的表面积
圆锥的侧面展开图是扇形
O
圆台的表面积
参照圆柱和圆锥的侧面展开图,试想象圆台的侧面展开图是什么
.
O
O’
圆台的侧面展开图是扇环
三者之间关系
O
O’
O
O
圆柱、圆锥、圆台三者的表面积公式之间有什么关系?
r’=r
上底扩大
r’=0
上底缩小
例2
如图,一个圆台形花盆盆口直径20
cm,盆底直径为15cm,底部渗水圆孔直径为1.5
cm,盆壁长15cm.那么花盆的表面积约是多少平方厘米(
取3.14,结果精确到1
)?
解:由圆台的表面积公式得
花盆的表面积:
答:花盆的表面积约是999
.
典型例题
课堂练习
1、一个三棱柱的底面是正三角形,边长为4,侧棱与底面垂直,侧棱长10,求其表面积.
2、一个圆台,上、下底面半径分别为10、20,母线与底面的夹角为60°,求圆台的表面积.
变式:求切割之前的圆锥的表面积
3、面积为2的菱形,绕其一边旋转一周所得几何体的表面积是多少?
4、若一个圆锥的轴截面是等边三角形,其面积为3,求这个圆锥的表面积
柱体、锥体、台体的体积
1、长方体的体积
D
A
B
C
D1
A1
B1
C1
等底等高柱体的体积相等吗?
2、柱体的体积
定理:等底等高柱体的体积相等
祖恒原理
将一个三棱柱按如图所示分解成三个三棱锥,那么这三个三棱锥的体积有什么关系?它们与三棱柱的体积有什么关系?
1
2
3
1
2
3
思考4:推广到一般的棱锥和圆锥,你猜想锥体的体积公式是什么?
高h
底面积S
3、锥体的体积
定理:等底等高锥体的体积相等
等底等高的棱柱和棱锥体积的关系
4、台体的体积
例3
有一堆规格相同的铁制六角螺帽共重5.8kg(铁的密度是7.8g/cm3),已知螺帽的底面是正六边形,边长为12mm,内孔直径为10mm,,高为10mm,问这堆螺帽大约有多少个?
求此棱柱挖去圆柱后的体积和表面积
引申:1.圆柱的侧面展开图如下左图所示,求此圆柱的体积。
侧面展开图
直观图1
直观图2
引申2:已知正四棱台两底面的边长,
和棱台体积,
求棱台的高.
